Kurs:Algorithmen und Datenstrukturen/Druckversion
Einleitung
BearbeitenAlgorithmen im Alltag
Bearbeiten- Bedienungsanleitungen
- Gebrauchsanleitungen
- Bauanleitungen
- Kochrezepte
- Berechnungsvorschriften (z.B. Berechnung der Fakultät)
Intuitive Begriffserklärung Algorithmus
Bearbeiten„Ein Algorithmus ist eine präzise (d.h. In einer festgelegten Sprache formulierten), endliche Beschreibung eines allgemeinen Verfahrens unter Verwendung ausführbarer elementarer Verarbeitungsschritte.“
Definitionen
BearbeitenAlgorithmus
- „systematische Verarbeitung“
- Eine eindeutige Beschreibung eines in mehreren Schritten durchgeführten Bearbeitungsvorgangs
- Ein Algorithmus ist ein allgemeines Verfahren zur Lösung eines Problems ohne Bezug auf einen konkreten Prozessor.
Programm
- Ein Programm ist eine konkrete Formulierung eines Algorithmus für eine konkrete Klasse von Prozessoren.
Prozessor
- Ein Prozessor ist etwas, das die Fähigkeit hat, Programme auszuführen.
Datenstrukturen
- „Ordnungsschema“
- Eine Struktur zur Verwaltung von Daten
- Darstellung von Informationen in maschinenverarbeitbarer Form
- Charakterisieren Daten und mögliche Operationen auf Daten
Transformationelle Probleme
BearbeitenEin Algorithmus definiert eine Transformation auf dem gesamten, durch die Eingaben definierten Zustand, aus dem als Bedeutung dann die Werte der Ausgabevariablen ausgelesen werden. Das heißt, ein Algorithmus benutzt kein weiteres Wissen neben der Eingabe und hat keine Seiteneffekte!
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 2.1 zu finden.
Eigenschaften von Algorithmen
BearbeitenEin Algorithmus heißt …
- terminierend, wenn er für alle zulässigen Schrittfolgen stets nach endlich vielen Schritten endet
- deterministisch, wenn in der Auswahl der Verarbeitungsschritte keine Freiheit besteht
- determiniert, wenn das Resultat eindeutig bestimmt ist
- sequenziell, wenn die Schritte stets hintereinander ausgeführt werden
- parallel oder neben läufig, wenn gewisse Verarbeitungsschritte nebeneinander (im Prinzip gleichzeitig) ausgeführt werden
- korrekt, wenn das Resultat stets korrekt ist
- effizient, wenn das Resultat in „annehmbarer“ Zeit geliefert wird
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 2.1.1 zu finden.
Algorithmenentwurf
BearbeitenDieses Kapitel behandelt die Vorgehensweise zum Algorithmenentwurf.
Vom Algorithmus zur Programmausführung
Bearbeiten- Der Algorithmus wird unabhängig von Programmiersprache und Rechnerhardware entworfen
- Der Algorithmus wird in einer höheren Programmiersprache, z.B. Java, programmiert
- Das Programm wird in Maschinensprache übersetzt
- Die CPU interpretiert den Maschinencode und das Programm wird ausgeführt

Vorgehensweise Algorithmus-Entwurf
Bearbeiten- Hintergrundwissen erwerben: Derjenige der ein Problem beschreibt ist oft nicht derjenige, der den Algorithmus entwirft, dadurch kommt es zu unklaren Aufgabenstellungen, unterschiedlichem Vorwissen und verschiedenen Annahmen.
- Problem definieren: Erfordert Hintergrundwissen und Übung in der Definition von Problemen
- Algorithmus entwerfen: Erfordert Wissen zu Algorithmen und Datenstrukturen
- Programm erstellen: Erfordert Wissen über Programmiersprache (Java) und Programmierung
- Lösung überprüfen: Erfordert methodisches Wissen zu Termination, Korrektheit und Effizienz
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 2 und 8.1 zu finden.
Größter gemeinsamer Teiler
BearbeitenIn diesem Kapitel wird die im vorherigen Kapitel vorgestellte Vorgehensweise zum Algorithmenentwurf am Beispiel des größten gemeinsamer Teilers gezeigt.
Hintergrundwissen
BearbeitenGegeben zwei positive natürliche Zahlen a und b, welche ist die größte positive natürliche Zahl x, so dass x sowohl a also auch b teilt und es keine positive natürliche Zahl x’ gibt, so dass x’ > x und x’ teilt sowohl a als auch b.
- Alle Variablen bezeichnen natürliche Zahlen größer 0
- Anwendungsbeispiel Kürzen: 52/32 hat 4 als ggT, mit 4 gekürzt ergibt sich 13/8
Problem definieren
BearbeitenWir betrachten (i. Allg.) hier transformationelle Probleme
Problem: ggT-Berechnung Eingabe: zwei Zahlen a,b ∈ N Ausgabe: der größte gemeinsame Teiler von a und b
Algorithmus definiert also eine Transformation auf dem gesamten, durch die Eingaben definierten Zustand, aus dem als Bedeutung dann die Werte der Ausgabevariablen ausgelesen werden.
Algorithmus entwerfen
BearbeitenVerfahren von Euklid (300 v. Chr.) für natürliche Zahlen:
"%" ist die Modulo Funktion:
ggT(46,18) = ggT(18,10) (α=2, b=18, r=10)
= ggT(10,8) (α=1, b=10, r=8)
= ggT(8,2) = 2 (α=1, b=8, r=2)
In Worten erklärt:
- Wie oft passt 18 in 46? → 2 mal (α)
- 2*18 ist 36, zur 46 fehlen somit noch 10 (r)
- Wie oft passt 10 in 18? → 1 mal (α)
- 1*10 ist 10, zur 18 fehlen somit noch 8 (r)
- Wie oft passt 8 in 10? → 1 mal (α)
- 1*8 ist 8, zur 10 fehlen somit noch 2 (r)
- 8 passt 0 mal in die 2, somit ist der ggT die 2
Idee: Führe die Berechnung von ggT(a,b) auf die Berechnung von ggT(b, a % b) zurück (falls b|a, ansonsten ist das Ergebnis b).
Vorbedingung: Eine Bedingung zur Ausführung des ggT(a,b) ist, dass a,b>0
Wie kann man dies sicherstellen?
- Optimistische Strategie
- Man geht vom Erfüllt sein der Bedingung aus
- z.B. Clients bekannt und zuverlässig, z.B. bei Rekursion
- Man geht vom Erfüllt sein der Bedingung aus
- Pessimistische Strategie
- Man überprüft die Bedingung bei jedem Aufruf
- z.B. Öffentliche APIs
- Man überprüft die Bedingung bei jedem Aufruf
- Möglichkeiten bei nicht erfüllten Vorbedingungen
- Ausnahmen werfen
- Parameter auf Defaultwerte setzen (mit Meldung)
- Programm nicht ausführen und Defaultwert zurückgeben
Programm erstellen
BearbeitenPseudocode
Algorithmus euklid
Eingabe: Ganze Zahlen a,b
Ausgabe: Ganze Zahl c=ggT(a,b)
Setze r = a % b;
Falls r = 0 gib b zurück;
Ansonsten gib euklid(b,r) zurück;
Rekursiv, optimistisch
public int ggT(int a, int b){
int r = a % b;
if (r == 0)!
return b;
else
return ggT(b,r);
}
Iterativ, pessimistisch – Version 1
public int ggT(int a, int b){
if (a<=0 || b<=0)
throw new ArithmeticError(“negative Daten bei ggT(“+a+“,“+b+“)“);
else {
int r = a % b;
while (r!=0) {
a = b;
b = r;
r = a % b;
}
return b;
}
}
Iterativ, pessimistisch – Version 2
public int ggT(int a, int b){
if (a<=0 || b<=0)
then throw new ArithmeticError(“negative Daten bei ggT(“+a+“,“+b+“)“);
else {
do{
int r = a % b;
a=b;
b=r;
} while (r!=0);
return a;
}
}
Algorithmenanalyse
BearbeitenIst unser ein Algorithmus ein guter Algorithmus?
- Wichtige Fragen:
– Terminiert der Algorithmus?
– Ist der Algorithmus korrekt?
– Welche Laufzeit hat der Algorithmus?
1. Theorem:
Für positive natürliche Zahlen a und b mit a > b, terminiert der Algorithmus Euklid nach endlich vielen Schritten.
Beweis:
(a) Falls b|a terminiert der Algorithmus in einem Schritt. (b) Andernfalls wird ein Parameter der Algorithmus um mindestens den Wert 1 verringert und der Algorithmus rekursiv aufgerufen. Spätestens wenn ein Parameter den Wert 1 erreicht tritt Fall (a) ein und der Algorithmus terminiert. Für endliche Eingaben bedeutet dies eine endliche Laufzeit. Was ist mit anderen Eingaben?
2. Theorem:
Der Algorithmus Euklid löst das Problem ggT.
Beweis:
Wir haben bereits festgestellt, dass für zwei positive natürliche Zahlen a, b gilt, dass ggT(a,b)=b (falls b|a) und ggT(a,b)=ggT(a%b) (falls b|a nicht gilt). Der Algorithmus Euklid vollzieht genau diese Fallunterscheidung nach.
3. Theorem:
Für positive natürliche Zahlen a und b mit a>b, benötigt der
Algorithmus Euklid maximal max{a,b} viele rekursive Aufrufe.
Beweis:
Wir haben bereits festgestellt, dass Euklid stets terminiert, dass bei jedem Aufruf ein Parameter um mindestens den Wert 1 verringert wird und dass wenn der zweite (stets kleinere) Parameter den Wert 1 hat die Rekursion spätestens endet. Damit kann es maximal max{a,b} viele rekursive Aufrufe geben.
Anmerkung:
Die obige Laufzeit ist nur eine grobe obere Abschätzung. Die tatsächliche Worst‐case‐Laufzeit ist O(log(ab)) (mehr zur O‐Notation später)
Fazit
BearbeitenWelche Strategie (optimistisch, pessimistisch) und welches Verhalten man bei nicht‐erfüllten Vorbedingungen zeigt, hängt von vielen Faktoren ab:
– Bei unkritischen oft aufzurufenden Algorithmen könnte die Überprüfung der Zulässigkeit zu viel Aufwand sein
– Bei zeitintensiven Algorithmen kann durch eine Überprüfung Zeit gespart werden
Man sollte das Verhalten seines Algorithmus im Fehlerfall aber stets gut dokumentieren!
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8 zu finden.
Berechenbarkeitsbegriff
BearbeitenEin Problem (z.B. eine mathematische Funktion) heißt berechenbar, falls dafür ein Algorithmus existiert.
- Berechenbar: Algorithmus stoppt nach endlich vielen Schritten
- Funktion f: W → V ist
- partiell: Def(f) ⊆ W (Beispiel: f: ℝ → ℝ, f(x)= 1/x)
- total: Def(f) = W
Ausgangssituation: Wir entwerfen und programmieren einen Algorithmus und wir haben eine Vorstellung was berechenbar ist (intuitiver Berechenbarkeitsbegriff). Das Problem ist nun, wie man diese Berechenbarkeit nachweisen kann. Dazu bringen wir die intuitive Form in eine mathematische Form und können diese mit mathematischen Beweisen belegen.
Formale Definitionen des Berechenbarkeitsbegriff: Turing berechenbare Funktionen, while-Programme, µ-rekursive Funktionen
Church-Turing-These
BearbeitenDie Klasse der Turing-berechenbaren Funktionen ist genau die Klasse der intuitiv berechenbaren Funktionen. Wobei "intuitiv" nicht exakt formalisierbar ist.
Die durchführbaren Algorithmen sind eine Teilmenge der berechenbaren Funktionen, welche wiederum eine Teilmenge aller existierenden Funktionen sind.

Beispiele
BearbeitenDurchführbare Algorithmen
- ggT, Matrizenmultiplikation, Zinsberechnung,…
Berechenbare Funktionen, die nicht durchführbar sind
- Harte Optimierungsprobleme mit Millionen von Variablen
- Vollständige Eigenwertberechnung auf dem Facebook-Graphen
Nicht berechenbare Funktionen
- Haltefunktion (gibt zu einem beliebigen Programm an, ob es hält)
- Äquivalenzfunktion (gibt zu zwei beliebigen Programmen an, ob sie das gleiche Verhalten haben)
- …
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 6.4 und 7.1 zu finden.
Überblick Theoretische Grundlagen
BearbeitenIn diesem Kapitel geben wir einen Überblick über die Theoretischen Grundlagen.
Ein Algorithmenentwurf ist eine kreative Disziplin. Es gibt keine allgemeingültige Anleitung zum Entwerfen und Analysieren von Algorithmen. Wir werden uns in dieser Vorlesung mit vielen Beispielen beschäftigen, die als Inspiration und Werkzeug dienen, weitere Algorithmen zu entwerfen. Einige theoretische Grundlagen sind allerdings notwendig. In diesem Kapitel beschäftigen wir uns näher mit
1. Programmierparadigmen
Was für Möglichkeiten gibt es Algorithmen zu entwickeln und zu implementieren?
2. Laufzeitanalysen
Wie kann man die Laufzeit eines Algorithmus analytisch ableiten und einordnen?
3. Entwurfsmuster
Was sind generelle Prinzipien für das Design eines Algorithmus?
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3 zu finden.
Paradigmenbegriff
BearbeitenIn diesem Kapitel erläutern wir den Paradigmenbegriff.
Definition
Bearbeiten„Unter einem Paradigma versteht man unter anderem in der Wissenschaftstheorie ein `Denkmuster, welches das wissenschaftliche Weltbild eine Zeit prägt´ - ein Algorithmenparadigma sollte daher ein Denkmuster darstellen, das die Formulierung und den Entwurf von Algorithmen und damit letztendlich von Programmiersprachen grundlegend prägt.“
Oder etwas kürzer: Ein Muster für den Entwurf und die Formulierung von Algorithmen.
Paradigmen zur Algorithmenkonstruktion
BearbeitenFunktional: Verallgemeinerung der Funktionsauswertung. Rekursion spielt eine wesentliche Rolle.
- f(x) := 2 g(x) + h(x)
- h(x) := 1 + h(x-1)
Logisch: basierend auf logischen Aussagen und Schlussfolgerungen
- „wenn a verwandt mit b und b verwandt mit c, dann ist a verwandt mit c“
Imperativ: basierend auf einem einfachen Maschinenmodell mit gespeicherten und änderbaren Werten. Primär werden Schleifen und Alternativen als Kontrollbausteine eingesetzt.
- „erst: erhöhe a, dann multipliziere b mit c, dann subtrahiere a mit c,….“
Objektorientiert: basierend auf Nachrichtenaustausch zwischen Objekten und Vererbung von Klassen
Beispiel Java: objektorientiert, imperativ, Elemente von funktional
Paradigmen und Programmiersprachen
BearbeitenFunktional
- Haskell, ML, Lisp (Datenauswertung,Datenbank)
Logisch
- Prolog (Datenbank)
Imperativ
- C, Pascal (maschinenorientiert )
Objektorientiert
- Smalltalk, Eiffel („Simulation“ verteilter Systeme), python
Mischungen
- C++, C#, Java
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3 zu finden.
Funktionale Algorithmen
BearbeitenIn diesem Kapitel wird die funktionale Programmierung behandelt.
Grundidee
BearbeitenDefinition zusammengesetzter Funktionen durch Terme mit Unbestimmten.
Ein Beispiel einer einfachen Funktionsdefinition ist .
Erinnerung Definition Term : *Variable ist ein Term *Konstanten-Symbol ist ein Term *Sind Terme und f ein n-stelliges Funktionssymbol, so ist ein Term
Beispiele für Terme
BearbeitenUnbestimmte (Symbole)
- … vom Typ int
- q,p,r … vom Typ bool
Terme mit Bestimmten
- 1+1, 3*2, ...
Terme mit Unbestimmten
- Terme vom Typ int
- x, x-2, 2x+1, (x+1)(y-1)
Terme vom Typ bool
Definition
BearbeitenEin funktionaler Algorithmus ist eine Menge von Funktionsdefinitionen bis mit:
...
Die erste Funktion wird wie beschrieben ausgewertet und ist die Bedeutung (=Semantik) des Algorithmus.
ist die zustands-bestimmende Eingabe aus der die Werte der Ausgabe abgelesen werden.
Funktionale Algorithmen sind die Grundlage einer Reihe von universellen Programmiersprachen, z.B. APL und Lisp. Diese Programmiersprachen werden als funktionale Programmiersprachen bezeichnet.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2 zu finden.
Funktionsdefinition und Signatur
BearbeitenIn diesem Kapitel wird die Funktionsdefinition und Signatur von funktionalen Algorithmen behandelt.
Funktionsdefinition
BearbeitenEine Funktion f ist eine Relation zwischen einer Eingabemenge X und einer Ausgabemenge mit der Eigenschaft:
Für alle x ∈ X, y,y‘ ∈ Y mit (x,y),(x,y‘) ∈ f gilt y=y‘
Wir schreiben dann üblicherweise f(x)=y anstatt(x,y)∈ f und deklarieren eine Funktion durch . Ist eine Funktion so heißt X Eingabemenge und Y Ausgabemenge. In der funktionalen Programmierung sind Ein‐ und Ausgabemengen üblicherweise Terme eines bestimmten Typs.
Termdefinition
BearbeitenSei T ein Typ, eine Menge von Variablen vom Typ T und eine Menge von Konstanten vom Typ T. Dann ist jedes ist ein Term vom Typ T, jedes ein Term vom Typ T und ist eine Funktion und sind Terme vom Typ T, so ist ein Term vom Typ T.
Beispiel Terme natürlicher Zahlen
BearbeitenSei int der Typ der natürlichen Zahlen, eine Menge von Variablen vom Typ und . Mögliche Funktionen auf natürliche Zahlen sind
- x
- x
3+4, (8+9)*10, X*4+1 sind dann Terme natürlicher Zahlen.
Beispiel Bool´sche Terme
BearbeitenSei bool der Typ der Bool´sche Terme, eine Menge von Variablen vom Typ und . Mögliche Funktionen auf Bool´sche Termes sind
- x
true und sind dann Bool´sche Terme.
Sind Unbestimmte vom Typ (bool oder int) und ist ein Term, so heißt eine Funktionsdefinition vom Typ T.
- T ist dabei der Typ des Terms ().
- f: ist der Funktionsname
- ist ein formaler Parameter
- : ist ein Funktionsausdruck
Beispiel
BearbeitenJede Funktionsdefinition hat das Schema Funktionsname(formale Parameter):= Funktionsausdruck
Signatur einer Funktion
BearbeitenEine Funktion f hat die folgende Funktionsdefinition:
mit sind vom Typ
ist vom Typ T
Die Signatur von f ist: mit der Struktur
Name mit Stelligkeit: Parameter mit Typ * ... * Parameter mit Typ → Typ des Rückgabewertes
Beispiel einer Funktionsdefinition
Bearbeiten- f(p,q,x,y) := if (p ∨ q) then 2x + 1 else 3y ‐1
- g(x) := if even(x) then x / 2 else 3x ‐1
- h(p,q) := if p then q else false, mit h als Funktionsname, (p,q) als formalen Parameter und dem darauffolgenden Funktionsausdruck.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2.2 zu finden.
Auswertung von Funktionen
BearbeitenIn diesem Kapitel wird die Auswertung funktionaler Algorithmen behandelt.
- Definierte Funktionen können mit konkreten Werten aufgerufen werden.
- Wir wissen, dass eine definierte Funktion folgende Struktur hat
- Sind nun konkrete Werte vom Typ , so ersetzt man in jedes Vorkommen der Unbestimmten mit . Somit kann der entstehende Term ausgewertet werden.
- Dabei heißen die konkreten Werte aktuelle Parameter.
- Ausdruck heißt Funktionsaufruf.
Beispiel
BearbeitenLiteratur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2.3 zu finden.
Auswertung von Funktionen
BearbeitenIn diesem Kapitel wird die Auswertung funktionaler Algorithmen behandelt.
- Definierte Funktionen können mit konkreten Werten aufgerufen werden.
- Wir wissen, dass eine definierte Funktion folgende Struktur hat
- Sind nun konkrete Werte vom Typ , so ersetzt man in jedes Vorkommen der Unbestimmten mit . Somit kann der entstehende Term ausgewertet werden.
- Dabei heißen die konkreten Werte aktuelle Parameter.
- Ausdruck heißt Funktionsaufruf.
Beispiel
BearbeitenLiteratur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2.3 zu finden.
Auswertung rekursiver Funktionen
BearbeitenIn diesem Kapitel wird die Auswertung rekursiver Funktionen behandelt.
Erweiterung der Funktionsdefinition
Bearbeiten- Erweiterung der Definition von Termen
- Neu: Aufrufe definierter Funktionen sind Terme
- Eine Funktionsdefinition f heißt rekursiv, wenn direkt oder indirekt (über andere Funktionen) ein Funktionsaufruf f(...)in ihrer Definition auftritt.
Gegeben ist die folgende Funktion:
Die Auswertung dieser Funktion lautet:
Auswertung rekursive Funktionsdefinition
BearbeitenGegeben ist folgende rekursive Funktion:
Die Auswertung dieser Funktion lautet:
Hier greift die erste Zeile der Funktionsdefinition. Da x=0 ist nehmen wir y
Hier greift die zweite Zeile der Funktionsdefinition. Da x>0 ist haben wir f(1-1,y)+1. Da x nach diesem Schritt null ist, greift nun die erste Zeile und wir erhalten y+1.
Hier greift ebenfalls die zweite Zeile der Funktionsdefinition. Da x>0 ist haben wir f(2-1,y)+1. Anschließend wenden wir noch einmal die zweite Zeile an, da x immer noch größer ist als null und wir erhalten f(1-1,y+1)+1. Da x nun null ist greift die erste Zeile der Funktionsdefinition und wir erhalten y+2.
...
Hier lässt sich bereits abschätzen, dass das Ergebnis der Funktion immer weiter hochgezählt wird und es lässt sich allgemein sagen:
Ist unser x negativ, entwickelt sich die Auswertung wie folgt:
Hier greift die dritte Zeile der Funktionsdefinition. Da x<0 ist werden die Vorzeichen umgekehrt. Nun, da x=1 ist, greift die zweite Zeile und wir erhalten -f(1-1,-y)+1. Da x nun null ist greift wieder die erste Zeile und wir erhalten y-1.
...
Auch hier lässt sich bereits abschätzen, wie sich die Funktion einwickelt und es lässt sich allgemein sagen:
Definiertheit
BearbeitenGegeben ist folgender Algorithmus:
Auf welchen Eingaben ist der Algorithmus definiert?
Auswertung:
- Diese Auswertung terminiert nicht!
Somit gilt:
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2.4 zu finden.
Definiertheit der Fakultätsfunktion
BearbeitenIm folgenden Beispiel wird die Definiertheit anhand des Beispiels der Fakultät gezeigt.
Es ist bekannt, dass und
- .
Für negative Werte sind Fakultäten nicht definiert.
1.Lösung
- Das bedeutet:
2.Lösung
- Das bedeutet:
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2.6 zu finden.
Größter gemeinsamer Teiler - funktional
BearbeitenIn folgendem Beispiel werden wir den größten gemeinsamen Teiler mit Hilfe eines funktionalen Algorithmus berechnen.
Hintergrundwissen
BearbeitenWir haben folgende funktionale Spezifikationen:
Auswertung
BearbeitenEine beispielhafte Auswertung sieht wie folgt aus:
Abbruchbedingungen und Rekursion
BearbeitenDer ggT lässt sich nur korrekt berechnen, wenn positive Eingaben gemacht werden. Bei negativen Eingaben ist der ggT undefiniert und der Algorithmus terminiert nicht.
- Abbruchbedingungen:
Im Fall des Abbruchs wird eine Evaluierung oder Ausnahme angegeben.
- Bedingungen für rekursive Verwendung der Funktion, "einfachste" Rekursion zuerst
Im Fall der Rekursion wird eine Evaluierung angegeben.
Programm
Bearbeitenpublic static int ggT(int x, int y)
{
if ((x <= 0) || (y <= 0))
throw new ArithmeticError(“negative Daten bei ggt“));
else if (x==y) then return x;
else
if x > y then return ggT(y,x);
else return ggT(x,y-x);
}
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2.6 zu finden.
Fibonacci Zahlen - funktional
BearbeitenIn folgendem Beispiel werden wir die Fibonacci-Zahlen mit Hilfe eines funktionalen Algorithmus berechnen.
Hintergrundwissen
BearbeitenBei den Fibonacci Zahlen handelt es sich um eine unendliche Zahlenreihe. Ursprünglich wurde die Fibonacci-Folge zur Beschreibung des Wachstums einer Kaninchenpopulation verwendet. Diese erfolgt progressiv. Am Anfang gibt es ein Kaninchenpaar, dieses wird im zweiten Monat zeugungsfähig und zeugt jeden Monat ein weiteres Paar Kaninchen. Keins der Kaninchen stirbt. Das heißt, die Summe der benachbarten Zahlen ergibt die nächste Zahl ( 0,1,1,2,3,5,8,...).
...
Programm
Bearbeitenfib(x) := if (x==0) then 0
else if (x==1) then 1
else fib(x-1) + fib(x-2)
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.2.6 zu finden.
{{:Kurs:Algorithmen und Datenstrukturen/Vorlesung/Weiteres Beispiel}
Logische Algorithmen
BearbeitenBei den logischen Algorithmen handelt es sich um ein deklaratives Programmierparadigma. Die logische Programmierung ist ähnlich wie die funktionale Programmierung. Es gibt keine schrittweise (=imperative) Abhandlung von Schritten. Logische Zusammenhänge werden in Form von Klauseln aufgestellt. Die logische Programmierung basiert auf Prädikatenlogik erster Stufe, im speziellen auf Hornlogik, auf welche in späteren Kapiteln genauer eingegangen wird. Die logische Programmierung wird in den Programmiersprachen Prolog und Answer Set Programming genutzt. In diesem Kurs betrachten wir die Programmiersprache Prolog.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.4 zu finden.
Prädikatenlogik und Hornlogik
BearbeitenIn diesem Kapitel werden die Grundlagen der Prädikatenlogik und Hornlogik erläutert.
Grundlagen
BearbeitenSei U eine Menge von Konstanten, V eine Menge von Variablen, und P eine Menge von Prädikatsymbolen.
- Ein Term ist entweder eine Konstante oder eine Variable (prinzipiell sind auch Funktionsterme möglich, werden hier aber ignoriert)
- X,Y,... sind Variablen (und Terme)
- anna, bob, dave,... sind Konstanten (und Terme)
- Ein Atom ist ein n-stelliges Prädikat, gefolgt von n Termen
- parent(bob,anna) ist ein Atom
- sibling(anna, X) ist ein Atom
- Eine atomare Konjunktion ist eine Menge von Atomen
- parent(X,anna) ∧ sibling(anna,Y) ∧ parent (anna,tina)
- Bei logischer Programmierung wird oft das Komma für die Konjunktion verwendet: parent (X,anna), sibling(anna,Y), parent(anna,tina)
- Eine Hornklausel ist eine Implikation einer atomaren Konjunktion zu einem Atom
- grandparent(X,Y) ⇐ parent(X,Z) ∧ parent(Z,Y)
- In Prolog: grandparent(X,Y) :- parent(X,Z), parent(Z,Y).
- Anmerkung: Ein Hornklausel ist eigentlich definiert als eine Disjunktion mit maximal einem positiven Atom
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.4.1 zu finden.
Prolog
BearbeitenEin Prolog-Programm ist eine Menge von Hornklauseln und Fakten (=Atome ohne Variablen)
Beispiel 1
Bearbeitengrandparent(X,Y) :- parent(X,Z), parent(Z,Y).
brother(X,Y) :- male(X), male(Y), parent(Z,X), parent(Z,Y).
hasUncle(X) :- parent(Y,X), brother(Y,_).
parent(bob, anna).
parent(carl, bob).
male(bob).
Anmerkung: „_“ ist eine beliebige (unbenannte) Variable
Beispiel 2
Bearbeitens(X,Y) :- r(X,Y), t(Y).
r(a,b). r(a,e). r(c,d).
t(b). t(d).
Anfragen
BearbeitenProlog ist eine Anfrage-basierte Programmiersprache. Das bedeutet jede Ausführung eines Prolog-Programms muss mit einer Anfrage parametrisiert werden.
Die Anfragen zu oben gezeigten Prolog Programm aus Beispiel 1 lauten:
?grandparent(carl,anna) → Antwort YES ?male(anna) → Antwort NO (Closed World Assumption)
Anfragen können aber auch Variablen enthalten, so wie in Beispiel 2.
?s(a,X) → Antwort X=b ?r(a,X) → Antwort X=b, X=e
Die Semantik logischer Programme leitet sich direkt von der klassisch logischen Semantik der Prädikatenlogik ab (siehe Logik-Vorlesung).
Techniken:
- Grundierung des Programms (ersetze Variablen durch alle Kombinationen von Konstanten) und aussagenlogische Verarbeitung
- Unifikation des Anfrageterms und Backtracking
Beispiel
BearbeitenProblem: Wegfindung in gerichteten Graphen
- Gegeben ein Graph mit Knoten
- Gibt es einen Weg zwischen Knoten (für beliebige i,j)?
Lösung als Prolog-Programm:
path(X,Y) :- edge(X,Y).
path(X,Y) :- path(Z,Y), edge (X,Z).
edge(a1,a2). edge(a2,a3). edge(a2,a4). edge(a5,a1).
Anfragen:
?path(a1,a3) → Antwort YES ?path(a5,X) → Antwort X=a1, X=a2, X=a3, X=a4 (alle von a5 erreichbare Knoten)
Logische vs. Funktionale Programmierung
BearbeitenHornklauseln sind Funktionen im Sinne von atomaren Operationen. Sie haben gemeinsam, dass sie die Rekursion als zentrales Paradigma haben und eine mathematische Basis. Zu den Unterschieden zählt, dass sie Atome entweder wahr oder falsch sind und dass die Funktionswerte beliebige Typen haben können.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.4.1 zu finden.
Liste
BearbeitenEine Liste ist entweder die leere Liste oder ein Term gefolgt von einer Liste.
Definition in Prolog
Bearbeitenlist([]). list([X|Y]) :- list(Y).
Der |-Operator trennt den Kopf (Head=erstes Element)einer Liste vom Rumpf (Tail=Restliste) ab
Beispiele
Bearbeiten- Liste von Zahlen:
[1|[2|[3]]] = [1,2,3]
- Liste von beliebigen Termen:
[male(bob), female(anna),male(carl)]
Listenmanipulation
Bearbeiten- Aneinanderreihung:
- append(X,Y,Z): X ist die Liste, die entsteht, wenn Z an Y angehängt wird
append(X,X,[]). append([Y|X], [Y|Z],L) :- append(X,Z,L).
- Invertierung:
- invert(X,Y): X ist die Invertierung von Y
invert([],[]). invert([X|Y],L) :- invert(Y,Z), append(L,Z,[X]).
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.4.1 zu finden.
Imperative Algorithmen
BearbeitenDie imperative Vorgehensweise ist eine verbreitete Art, um Algorithmen für Computer zu formulieren. Sie basiert auf den Konzepten Anweisung und Variablen und wird durch Programmiersprachen wie Java, C, PASCAL, FORTRAN, COBOL, Maschinencode, … realisiert. Das Prinzip ist ein abstraktes Rechnermodell. Werte werden gespeichert und anschließend schrittweise bearbeitet. Imperative Algorithmen sind nicht so elegant, verständlich und wartbar wie funktionale, objektorientierte oder logische Algorithmen.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3 zu finden.
Variablen
BearbeitenEine Variable besteht aus einem Namen (z.B. X), einem veränderlichen Wert und einem Typ. Bei Variablen handelt es sich um Speicherplätze für Werte. Ist t ein Term ohne Variablen und w(t) sein Wert, dann heißt das Paar X:=t eine Wertzuweisung. Ihre Bedeutung ist festgelegt durch
Nach Ausführung von X:=t gilt X=w(t) Vor Ausführung der ersten Wertzuweisung gilt X=?(undefiniert)
Beispiel
Bearbeiten
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3.1 zu finden.
Zustände
BearbeitenIst eine Menge von Variablen (-namen) von denen alle nur Werte aus der Wertemenge W haben können (alle Variablen vom gleichen Typ), dann ist der Zustand Z eine partielle Abbildung.
(Zuordnung des momentanen Wertes)
- Beispiel in einem gewissen Zustand
- Nach folgt:
Ist ein Zustand und wählt man eine Variable X und einen Wert w aus dem Wertebereich W, so ist der transformierte Zustand wie folgt definiert:
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3.1 zu finden.
Anweisungen
BearbeitenIn diesem Kapitel behandelt wir das Thema Anweisungen.
Arten von Anweisungen
BearbeitenDabei unterscheiden wir in zwei verschiedene Anweisungsarten. Zum einen die elementaren Anweisungen wie Wertezuweisungen und zum anderen die komplexen Anweisungen.
Semantik einer Anweisung
BearbeitenFunktion, die einen Zustand in einen neuen Zustand überführt.
Allgemein gesagt ist es die Wirkungsweise von auf den Zustand Z
Beispiele Zuweisung als Anweisung
BearbeitenBeispiel 1
BearbeitenEin Beispiel ist die Wertezuweisung:
ist eine elementare Anweisung
Diese Wertezuweisung transformiert in eine Funktion auf Zustände sieht wie folgt aus:
Die Zuweisung berechnet den neuen Zustand.
Der alte Zustand ist und der neue Zustand ist
Beispiel 2
BearbeitenEin weiteres Beispiel ist die Zuweisung mit gleichen Variablen auf beiden Seiten.
Die Transformation in eine Funktion auf Zustände lautet:
Bei der letzten Anweisung handelt es sich nicht um eine rekursive Gleichung! An dieser Stelle sei vermerkt, dass Wertezuweisungen die einzigen elementaren Anweisungen sind.
Komplexe Anweisungen
BearbeitenBisher haben wir elementare Anweisungen (Wertzuweisungen) als Funktionen auf Zustände verstanden. Komplexe Anweisungen nehmen Konstrukte bzw. Bausteine von imperativen Algorithmen. Diese Bausteine sind
- Sequenz
- Auswahl/Selektion
- Iteration
Die Semantik wird wiederum durch Konstruktion von Funktionen definiert. Iteration ist das Gegenstück zu rekursiven Funktionsaufrufen bei funktionalen Algorithmen
Sequenz
BearbeitenSequenzen, oder auch Folgen, sind und Anweisungen, so ist auch eine Anweisung. Die Zustandstransformation beschreibt die Semantik der Sequenz.
Die Semantik ist das Schachteln der Funktionsaufrufe und das daraus folgende hintereinander ausführen der beiden Funktionen.
Selektion
BearbeitenEine Selektion, bzw. eine Auswahl, liegt beispielsweise vor, wenn und Anweisungen sind und B ein boolescher Ausdruck ist, dann ist auch
eine Anweisung.
Die zugehörige Zustandstransformation ist:
Voraussetzung ist, dass Z(B) definiert ist, sonst ist die Bedeutung der Auswahlanweisung undefiniert.
Iteration
BearbeitenWiederholung (Iteration, Schleife):
Ist α eine Anweisung und B ein boolescher Ausdruck, so ist: while B do α auch eine Anweisung
Zustandstransformation:
Ist Z(B) undefiniert, so ist die Bedeutung dieser Anweisung ebenfalls undefiniert.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3.1 und 3.3.2 zu finden.
Syntax und Semantik
BearbeitenIn diesem Kapitel wird die Syntax und Semantik von imperativen Algorithmen behandelt.
Umsetzung in Programmiersprachen
BearbeitenIn realen imperativen Programmiersprachen gibt es fast immer diese Anweisungen, da imperative Algorithmen die Grundbausteine imperativer Programmiersprachen sind. While-Schleifen sind rekursiv definiert, ihre rekursive Auswertung braucht nicht zu terminieren. Bereits Programmiersprachen mit diesen Sprachelementen sind universell. Wir werden uns hier zunächst auf die Datentypen bool und int beschränken und können nun die Syntax imperativer Algorithmen festlegen.
Syntax
Bearbeiten<Programmname>: var X,Y,...:int; P,Q,...:bool; (Variablen Deklaration) input (Eingabe Variablen) (Anweisungen) output (Ausgabe-Variablen)
Semantik
BearbeitenDie Festlegung der formalen Bedeutung ist hier etwas komplexer als bei den funktionalen Algorithmen. Das Ziel ist aber das gleiche: Die Funktion zur Semantikfestlegung.
Die Bedeutung (Semantik) eines imperativen Algorithmus ist eine partielle Funktion:
Es gilt:
Programme Wertebereich der Typen von Wertebereich der Typen von
Das bedeutet, dass der Algorithmus eine Transformation auf den gesamten initialen Zustand (geg. durch die Eingabe)definiert. Die Bedeutung gibt die Werte der Ausgabevariablen an.
Die Funktion Z ist nicht definiert, falls die Auswertung von nicht terminiert.
Charakterisierung
BearbeitenDie Algorithmenausführung imperativer Algorithmen besteht aus einer Folge von Basisschritten, oder genauer gesagt Wertzuweisungen. Diese Folge wird mittels Selektion und Iteration basierend auf booleschen Tests über dem Zustand konstruiert. Jeder Basisschritt definiert eine Transformation des Zustands. Die Semantik des Algorithmus ist durch die Kombination all dieser Zustandstransformationen zu einer Gesamttransformation festgelegt.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3.2 zu finden.
Fakultätsfunktion als imperativer Algorithmus
BearbeitenIm Folgenden werden wir die Fakultätsfunktion als imperativen Algorithmus entwerfen.
Hintergrundwissen
BearbeitenFakultätsfunktion:
Es ist:
Falls die Bedingung der while-Schleife lautet, dann ist:
Gesucht ist das Ergebnis des Aufrufs FAC(3).
Die Abkürzung der while für die Zeile ist
Die Signatur der Semantikfunktion ist
Die Funktion ist durch Lesen von Y im Endzustand Z definiert
Der Endzustand ist definiert durch
, wobei die Folge aller Anweisungen des Algorithmus ist.
Der initiale Zustand ist definiert als
Die Zustände abkürzend ohne Variablennamen sind
Die Auswertung
Bearbeiten
Schlussfolgerung
BearbeitenDas bedeutet
- ...
Damit gilt
Beobachtungen
BearbeitenDer Übergang von der 3. auf die 4. Zeile folgt der Definition der Sequenz, indem der Sequenzoperator in einen geschachtelten Funktionsaufruf umgesetzt wird. Nur in der 5. Zeile wurde eine Wertzuweisung formal umgesetzt,später sind sie einfach verkürzt direkt ausgerechnet. In der 7. Zeile haben wir die Originaldefinition der Iteration eingesetzt (nur mit Kürzel α' statt α, da α bereits verwendet wurde). Dies entspricht im Beispiel α' = {Y:= Y · X; X:= X - 1}. Das Z in der 7. und 8. Zeile steht für den Zustand (3,1). (In späteren Zeilen analog für den jeweils aktuellen Zustand.)Bei diesem Beispiel sieht man folgendes sehr deutlich: Die Ausführung einer while-Schleife erfolgt analog zur rekursiven Funktionsdefinition!
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3.3 zu finden.
Fibonacci Zahlen: Funktional vs. Imperativ
BearbeitenIn diesem Kapitel werden wir den funktionalen Algorithmus der Fibonacci-Zahlen mit dem imperativen Algorithmus vergleichen.
Funktionale Umsetzung
fib(x) := if (x==0) then 0
else if (x==1) then 1
else fib(x-1) + fib(x-2)
Imperative Umsetzung
FIB var X,A,B,C: int;
input X;
A := 0; B:=1; C:=1;
while X > 0 {
C := A+B;
A := B;
B := C;
X := X-1;
}
output A;
Für beliebige X gibt die Auswertung das Ergebnis von FIB(X). Wir erkennen, der imperative Algorithmus FIB berechnet folgende Funktion:
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3.3 zu finden.
ggT: Funktional vs. Imperativ
BearbeitenIn diesem Kapitel werden wir den funktionalen Algorithmus des größten gemeinsamen Teilers mit dem imperativen Algorithmus vergleichen.
Version 1
BearbeitenGGT1 var X,Y: int;
input X,Y;
while X ≠ Y {
while X > Y { X := X-Y; }
while X < Y { Y := Y-X; }
}
output X;
Die Auswertung für X=19 und Y=5 lautet:
| X | Y |
| 19 | 5 |
| 14 | 5 |
| 9 | 5 |
| 4 | 5 |
| 4 | 1 |
| 3 | 1 |
| 2 | 1 |
| 1 | 1 |
Die Berechnung erfolgt durch die Subtraktion der jeweils kleineren Zahl. Es ist zu Beobachten, dass der ggT mittels Subtraktion nicht effizient berechnet werden kann.
Version 2
BearbeitenGGT2 var X,Y,R: int;
input X,Y;
R := 1
while R ≠ 0 {
R := X % Y; X := Y; Y := R;
}
output X;
Die Auswertung für X=19 und Y=5 lautet:
| X | Y | R |
| 19 | 5 | 1 |
| 5 | 4 | 4 |
| 4 | 1 | 1 |
| 1 | 0 | 0 |
Die Auswertung für X=2 und Y=1000 lautet:
| X | Y | R |
| 2 | 1000 | 2 |
| 2 | 0 | 0 |
Die Berechnung erfolgt hier durch die Modulo Funktion. Falls X<Y sein sollte, werden X und Y erst vertauscht, wie in der zweiten Auswertung.
Dieser Algorithmus ist folgendermaßen definiert:
Vergleich
BearbeitenIntuitiv ist GGT2 schneller als GGT1, was man durch die Komplexität von Algorithmen zeigen kann.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 3.3.3 zu finden.
Komplexität
BearbeitenAuf dieser Seite wird das Thema Komplexität behandelt. Gegeben ist ein zu lösendes Problem. Es ist wünschenswert, dass der Algorithmus zur Berechnung der Lösung einen möglichst geringen Aufwand hat. Daher wird der Aufwand des Algorithmus (Komplexität) abgeschätzt . Zur Lösung von Problemen einer bestimmten Klasse gibt es einen Mindestaufwand.
Motivierendes Beispiel
BearbeitenAls Beispiel nutzen wir die sequentielle Suche in Folgen. Gegeben ist die Zahl b und n Zahlen, z.B. mit A[0...n-1] mit n>0, wobei die Zahlen verschieden sind. Gesucht ist ein Index , falls der Index existiert, sonst ist i = n. Die Lösung für das Problem ist:
i = 0;
while (i < n && b != A[i])
i++;
Der Aufwand der Suche hängt nun von der Eingabe ab, d.h vom gewählten Wert n, den Zahlen A[0],...,A[n] und von b. Es gibt zwei Möglichkeiten, eine erfolgreiche oder eine erfolglose Suche. Eine erfolgreiche Suche haben wir, wenn b=A[i] dann ist S=i+1 Schritte. Ist die Suche jedoch erfolglos, dann ist S=n+1 Schritte. Das Problem ist, dass die Aussage von zu vielen Parametern abhängt und unser Ziel ist eine globale Aussage zu finden, die nur von einer einfachen Größe abhängt, z.B. der Länge n der Folge.
Analyse erfolgreiche Suche
BearbeitenIm schlechtesten Fall wird b erst im letzten Schritt gefunden, d.h. b=A[n-1]. Dann wäre S=n. Im Mittel wird die Anwendung mit verschiedenen Eingaben wiederholt. Wenn man beobachtet wie oft b an erster, zweiter,..., letzter Stelle gefunden wird, hat man eine Annahme über die Häufigkeit. Läuft der Algorithmus k mal (k>1), so wird b gleich oft an erster, zweiter,....,letzter Stelle gefunden und somit k/n mal an jeder Stelle. Die Anzahl der Schritte insgesamt für k Suchvorgänge lässt sich folgendermaßen berechnen:
Für eine Suche benötigt man Schritte Daraus folgt, dass im Mittel ( bei einer Gleichverteilung)
Asymptotische Analyse
BearbeitenZur Analyse der Komplexität geben wir eine Funktion als Maß für den Aufwand an. . Das bedeutet f(n)=a bei Problemen der Größe n beträgt der Aufwand a. Die Problemgröße ist der Umfang der Eingabe, wie z.B. die Anzahl der zu sortierenden oder zu durchsuchenden Elemente. Der Aufwand ist die Rechenzeit( Abschätzung der Anzahl der Operationen, wie z.B. Vergleiche) und der Speicherplatz.
Aufwand für Schleifen
BearbeitenWie oft wird die Wertezuweisung x=x+1 in folgenden Anweisungen ausgeführt?
x = x +1
1-mal
for (i = 1; i <= n; i++)
x = x + 1;
n-mal
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
x = x + 1;
-mal
Aufwandsfunktion
BearbeitenDie Aufwandsfunktion ist meist nicht exakt bestimmbar. Daher wird der Aufwand im schlechtesten Fall und im mittleren Fall abgeschätzt und die Größenordnung ungefähr errechnet.
Vergleich Größenordnung
Bearbeiten| Funktion | n=100 | n=10.000 | n=100.000 |
| log n | 4,6 | 9,2 | 11,5 |
| 10.000 | 100.000.000 | 10.000.000.000 | |
| 1.000.000 |
Problemstellung
BearbeitenWie können wir das Wachstum von Funktionen abschätzen und wie verhalten sich die Funktionen zueinander? Das Ziel ist, die Funktion zu wählen, die nach oben beschränkt.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3 zu finden.
O-Notation
BearbeitenAuf dieser Seite wird die O-Notation behandelt. Bei der O-Notation werden die asymptotischen oberen Schranke für Aufwandsfunktion angegeben. Das heißt deren Wachstumsgeschwindigkeit bzw. Größenordnung. Eine Asymptote ist eine Gerade, der sich eine Kurve bei immer größer werdender Entfernung vom Koordinatenursprung unbegrenzt nähert. Eine einfache Vergleichsfunktion ist für Aufwandsfunktionen mit
Definition
BearbeitenFür eine Funktion ist die Menge wie folgt definiert:
Anschaulich formuliert bedeutet das, dass O(f(n)) die Menge aller durch f nach oben beschränkter Funktionen ist und somit die asymptotische obere Schranke ist.
Die Definition veranschaulichst sieht folgendermaßen aus:
Das heißt g wächst nicht schneller als f. Das bedeutet wiederrum ist für genügend große n durch eine Konstante c nach oben beschränkt.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.2 zu finden.
-Notation
BearbeitenFür eine Funktion ist die Menge wie folgt definiert:
Anschaulich formuliert bedeutet das, dass die Menge aller durch f nach unten beschränkter Funktionen ist und somit die asymptotische untere Schranke ist.
-Notation
BearbeitenDie exakte Ordnung von f(n) ist definiert als:
Oder etwas kompakter:
Anschaulich formuliert bedeutet das, dass die Menge aller durch f nach unten und oben beschränkter Funktionen und somit die asymptotische untere und obere Schranke ist.
Beweis
BearbeitenZu zeigen:
Zeige
Beispiel 1
BearbeitenWir stellen uns die Frage, ob bzw. ob eine obere Schranke für ist. Die Antwort ist ja. Die Begründung dazu lautet folgendermaßen:
Beispiel 2
BearbeitenWir stellen uns die Frage, ob bzw. ob eine obere Schranke für ist. Die Antwort ist nein. Beweisen kann man das durch Widerspruch. Unsere Annahme ist:
Wähle Widerspruch!!
Lemma
BearbeitenFür beliebige Funktionen f,g gilt:
Beweis in beide Richtungen
Bearbeiten
Als erstes machen wir den Beweis nach rechts ()
nun der Beweis nach links ()
Beispiel
Bearbeiten
Lemma
Bearbeiten1. 2. 3.
Beweis in beide Richtungen
BearbeitenBeweis zu 1. nach rechts ()
Beweis zu 1. nach links ()
(siehe Definition)
und sei t(n) ein beliebiges Element der Menge O(f(n))
(siehe Definition)
(Definition der Teilmenge, da t(n) ein beliebiges Element ist)
Beispiele
Bearbeiten
Damit ist
Damit ist
Damit ist
Lemma
BearbeitenFalls , dann ist auch .
Beweis
Bearbeiten
Dabei ist eine Konstante.
Beispiel
Bearbeiten
Lemma
Bearbeiten1. 2.
Ein häufiges Problem sind Grenzwerte der Art oder Bei diesem Problem kann man als Ansatz die Regel von de l'Hospital verwenden.
Satz(Regel von de L'Hospital) Seien f und g auf dem Intervall differenzierbar. Es gelte und es existiere . Dann existiert auch und es gilt:
Beispiel
Bearbeiten1.
2.
Beim zweiten Beispiel musste die Regel von de l'Hospital wiederholt angewandt werden.
Lemma
BearbeitenGibt es immer eine Ordnung zwischen den Funktionen? Es gibt Funktionen f und g mit . Ein Beispiel sind die Funktionen sin(n) und cos(n).
Für alle
Beweis durch Widerspruch
BearbeitenWir nehmen an, dass ,
das heißt .
Aber es muss auch gelten,
das heißt
Komplexitätsklassen
BearbeitenAuf dieser Seite werden die Komplexitätsklassen behandelt.
Wir sagen sei Und wir sagen, ein Algorithmus mit Komplexität f(n) benötigt höchstens polynomielle Rechenzeit, falls es ein Polynom p(n) gibt, mit . Des weiteren sagen wir, dass ein Algorithmus höchstens exponentielle Rechenzeit benötigt, falls es eine Konstante gibt, mit .
Die Komplexitätsklassen sind:
| der konstante Aufwand, das bedeutet der Aufwand ist nicht abhängig von der Eingabe | |
| der logarithmische Aufwand | |
| der lineare Aufwand | |
| der quadratische Aufwand | |
| der polynomiale Aufwand | |
| der exponentielle Aufwand |
Wachstum
Bearbeiten| f(n) | n=2 | ||||
| ldn | 1 | 4 | 8 | 10 | 20 |
| n | 2 | 16 | 256 | 1024 | 1048576 |
| 2 | 64 | 2048 | 10240 | 20971520 | |
| 4 | 256 | 65536 | 1048576 | ||
| 8 | 4096 | 16777200 | |||
| 4 | 65536 |
Zeitaufwand
BearbeitenNun stellen wir uns die Frage, wie groß bezüglich der Rechenschritte darf, oder kann ein Problem sein, je nach Komplexitätsklasse, wenn die Zeit T begrenzt ist? Wir nehmen an, dass wir pro Schritt eine Rechenzeit von brauchen. In der folgenden Tabelle steht T für die Zeitbegrenzung und G für die maximale Problemgröße.
| G | T=1Min. | 1 Std. | 1 Tag | 1 Woche | 1 Jahr |
| n | |||||
| 7750 | |||||
| 391 | 1530 | 4420 | 8450 | 31600 | |
| 25 | 31 | 36 | 39 | 44 |
Ein Beispiel ist für T=1 Min. :
Typische Problemklassen
Bearbeiten| Aufwand | Problemklasse |
|---|---|
| für einige Suchverfahren für Tabellen (Hashing) | |
| für allgemeine Suchverfahren für Tabellen (Baum-Suchverfahren) | |
| für sequenzielle Suche, Suche in Texten, syntaktische Analyse von Programmen (bei "guter" Grammatik) | |
| für Sortieren | |
| für einige dynamische Optimierungsverfahren (z.B. optimale Suchbäume), einfache Multiplikation von Matrix-Vektor | |
| für einfache Matrizen Multiplikationen | |
| für viele Optimierungsprobleme (z.B. optimale Schaltwerke), automatisches Beweisen (im Prädikatenkalkül 1.Stufe) |
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.3 zu finden.
Aufwandsanalyse von iterativen Algorithmen
BearbeitenAuf dieser Seite wird der Aufwand von iterativen Algorithmen analysiert. Als Aufwand wird die Anzahl der durchlaufenen Operationen zur Lösung des Problems bezeichnet ( Zuweisungen, Vergleiche...). Häufig ist der Aufwand abhängig vom Eingabeparameter (Problemgröße). Die Aufwandsklasse sagt, wie der Aufwand in Abhängigkeit von der Problemgröße wächst. Doch wie kann man nun bei beliebigem Java Code die Aufwandsklasse bestimmen?
Aufwand von Programmen ablesen
Bearbeitenvoid alg1(int n){
int m = 2;
int i;
int k = n;
while (n > 0){
i = k;
while (i > 0) {
m = m + i;
i = i / 2;
}
n = n - 1;
}
}
Die Aufwandsklasse ist . Die äußere Schleife wird n-mal durchlaufen und die Innere Schleife log n-mal.
void alg1(int n) {
int m = 1;
int i = 0;
while (m < n) {
while (i < m)
i = i + 1;
m = m + i;
}
}
Hier ist die Aufwandsklasse O(n+log n). In jedem Durchlauf der äußeren Schleife wird m verdoppelt, d.h. sie läuft log n Mal. Die innere Schleife läuft bis n/2, aber nicht jedes Mal, weil i nur ein Mal auf 0 gesetzt wird. Man könnte als Aufwandsklasse auch O(n) sagen, da der Summand log n nicht ins Gewicht fällt.
Bestandteile iterativer Algorithmen
BearbeitenZum einen haben wir elementare Anweisungen wie Zuweisungen und Vergleiche. Diese haben einen Aufwand von 1.
Des Weiteren haben wir Sequenzen oder auch geschrieben. Die obere Grenze ist und die untere Grenze ist . Dabei ist der Aufwand, der bei der Ausführung von entsteht.
Ein weiterer Bestandteil ist die Selektion. . Hier ist die obere Grenze und die untere Grenze .
Außerdem haben wir Iterationen . Hierbei ist die obere und die untere Grenze die Anzahl der Schleifendurchläufe, und die untere Grenze . Doch wie ist der Aufwand für eine for-Schleife? Ein Beispiel ist . Die Antwort ist die Abbildung auf eine while-Schleife.
while(B) {
}
Beispiel Sequenz
Bearbeitenpublic int berechne(int n) {
int x = 0;
x = x + 1;
return x;
}
Jede Zeile hat den Aufwand . Wie viele Operationen werden nun durchlaufen? Und ist die Anzahl abhängig vom Eingabeparameter? Der Aufwand ist
Die Aufwandsklasse ist somit
Beispiel Schleifen
Bearbeitenpublic int berechne(int n) {
int x = 0;
for (int i=0; i < n; i++) {
x = x + 1;
}
return x;
}
Die for Schleife hat den Aufwand . Die Initialisierung und das return haben jeweils den Aufwand .
Der Gesamtaufwand ist somit . Somit ist die Aufwandsklasse .
public int berechne(int n) {
int x = 0;
for (int i=0; i < n; i++) {
for (int j=0; j < n; j++) {
x = x + 1;
}
}
return x;
}
Hier hat die for-Schleife den Aufwand und die Initialisierung und das return wieder . Damit ergibt der sich Gesamtaufwand . Daraus folgt die Aufwandsklasse .
Beispiel Selektion
Bearbeitenpublic int berechne(int n) {
if (n % 2 == 0) {
int x = 0;
for (int i=0; i < n; i++) {
x = x + 1;
}
return x;
}else{
return n;
}
}
Hier hat die for-Schleife einen Aufwand von . Die Initialisierung und das return wieder .
Die obere Grenze ist somit und die untere Grenze
Faustregeln
BearbeitenZu den häufig verwendeten Faustregeln gehört, dass wenn wir keine Schleife haben, der Aufwand konstant ist. Eine weitere ist, dass bei einer Schleife immer ein linearer Aufwand vorliegt. Bei zwei geschachtelten Schleifen haben wir immer einen quadratischen Aufwand. Doch die Faustegeln gelten nicht ohne Ausnahmen. Besonders Acht geben muss man bei Aufwandsbestimmungen für Schleifen, bei mehreren Eingabevariablen, bei Funktionsaufrufen und bei Rekursionen.
Aufwandsbestimmung für Schleifen
Bearbeitenpublic int berechne(int n) {
int x = 0;
for (int i=0; i < 5; i++) {
x = x + 1;
}
return x;
}
Der Schleifenabbruch hängt nicht vom Eingabeparameter ab. Der Aufwand beträgt somit haben wir die Aufwandsklasse
public int berechne(int n) {
int x = 0;
for (int i=1; i < n; i = 2*i) {
x = x + 1;
}
return x;
}
Hier wächst die Laufvariable nicht linear an.Daher ist der Aufwand und wir haben die Aufwandsklasse .
Doch gibt es eine allgemeine Methodik zum Bestimmen des Schleifenaufwands?
for (int i=1; i < n; i=2*i) {
x = x + 1;
}
Schritt 1: Wie entwickelt sich hier die Laufvariable? Der Startwert i ist 1 und die Veränderung in jedem Schritt ist . Die Laufvariable entwickelt sich somit wie folgt:
Nach dem 1. Durchlauf
Nach dem 2. Durchlauf
Nach dem 3. Durchlauf
Nach dem k. Durchlauf
Schritt 2: Nach wie vielen Durchläufen wird die Schleife abgebrochen?
Der Abbruch erfolgt, wenn
:
Somit erfolgt ein Abbruch nach ⌈ ⌉ Durchläufen.
public int berechne(int[] f1, int[] f2) {
int result = 0;
for (int i=0; i < f1.length; i++) {
for (int j=0; j < f2.length; j++) {
if (f1[i] == f2[j]) result++;
}
}
return result;
}
Hier haben wir nun eine for Schleife mit mehreren Eingabevariablen. Die Problemgrößen sind .
public int berechne2(int[] f1, int[] f2){
f2 = mergeSort(f2);
int result = 0;
for (int i=0; i < f1.length; i++) {
if (binarySearch(f2, f1[i])) result++;
}
return result;
}
Der Aufwand ist hier . Somit ist die Aufwandsklasse .
In diesem Beispiel haben wir wieder mehreren Eingabevariablen. Diese sind die gleichen Problemgrößen .
public int berechne2(int[] f1, int[] f2){
int result = 0;
for (int i=0; i < f1.length; i++) {
for (int j=0; j < f2.length; j++) {
if (f1[i] == f2[j]) result++;
}
}
return result;
}
Der Aufwand ist hier wie folgt: . Somit ist die Aufwandsklasse .
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.4 zu finden.
Aufwandsanalyse von rekursiven Algorithmen
BearbeitenAuf dieser Seite wird der Aufwand von rekursiven Algorithmen untersucht.
public int fib(int n) {
if (n == 0 || n == 1) {
return 1;
} else {
return fib(n-1) + fib(n-2);
}
}
Wie ist nun der Aufwand für Fibonacci? Bei Rekursionsabbruch und im Rekursionsfall . Zur Bestimmung benutzen wir Rekursionsgleichungen.
Rekursionsgleichungen
BearbeitenEine Rekursionsgleichung ist eine Gleichung oder Ungleichung, die eine Funktion anhand ihrer Anwendung auf kleinere Werte beschreibt.
Rekursionsgleichung für Fibonacci:
Lösung von Rekursionsgleichungen
BearbeitenDie Frage ist nun, welche Aufwandklasse T(n) beschreibt. Dies könnten alle möglichen Aufwandsklassen sein. Methoden um dieses Problem zu lösen, sind die vollständige Induktion und das Master-Theorem.
Spezialfall Divide and Conquer Algorithmus
BearbeitenEin Divide-and-Conquer Algorithmus stellt im Allgemeinen eine einfache, rekursive Version eines Algorithmus dar und hat drei Schritte:
- Divide: Unterteile das Problem in eine Zahl von Teilproblemen
- Conquer: Löse das Teilproblem rekursiv. Wenn das
Teilproblem klein genug ist, dann löse das Teilproblem direkt (z.B. bei leeren oder einelementigen Listen)
- Combine: Die Lösungen der Teilprobleme werden zu einer Gesamtlösung kombiniert.
Merge Sort ist beispielsweise ein Divide and Conquer Algorithmus.
- Divide: Zerteile eine Folge mit n Elementen in zwei Folgen mit je n/2 Elementen.
- Conquer: Wenn die resultierende Folge 1 oder 0 Elemente enthält, dann ist sie sortiert.Ansonsten wende Merge Sort rekursiv an.
- Combine: Mische die zwei sortierten Teilfolgen.
public List mergeSort(List f) {
if (f.size() <= 1) {
return f;
} else {
int m = f.size() / 2;
List left = mergeSort(f.subList(0,m));
List right = mergeSort(f.subList(m,f.size());
return merge(left, right);
}
}
Die dazugehörige Rekursionsgleichung lautet:
Im Allgemeinen ist die Rekursionsgleichung für Divide and Conquer Algorithmen:
mit D(n) als Aufwand für Divide, T(n/b) als Aufwand für Conquer und C(n) als Aufwand für Combine.
Ab- und Aufrunden
BearbeitenDie Rekursionsgleichung von MergeSort beschreibt den Aufwand für den schlechtesten Fall.
Aber die Annahme, dass n eine geeignete ganze Zahl ist ergibt normalerweise das gleiche Ergebnis wie
eine beliebige Zahl mit Auf- bzw. Abrunden. Dies führt zur einfacheren Rekursionsgleichung:
Beispiel Binäre Suche
Bearbeitenpublic List binarySearch(ArrayList<Integer> f, int e) {
if (f.size() == 0) {
return -1;
} else {
int m = f.size() / 2;
if (f.get(m) == e) {
return m;
} else if (f.get(m) < e) {
return binarySearch(f.subList(0, m), e);
} else {
return binarySearch(f.subList(m+1, f.size()), e);
}
}
}
Die Rekursionsgleichung lautet
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.4 zu finden.
Vollständige Induktion
BearbeitenAuf dieser Seite wird die vollständige Induktion behandelt. Es handelt sich hierbei um eine rekursive Beweistechnik aus der Mathematik. Sie ist gut geeignet, um Eigenschaften von rekursiv definierten Funktionen zu beweisen.
Vorgehen
BearbeitenZunächst vermutet man eine Eigenschaft (z.B. Aufwandsklasse einer Rekursionsgleichung). Nun folgt der Induktionsanfang: Eigenschaft hält für ein kleines n. Als nächstes folgt der Induktionsschritt: Die Annahme ist, dass wir es bereits für ein kleineres n gezeigt haben und wenn die Eigenschaft für kleinere n hält, dann hält sie auch für das nächstgrößere n!
Beispiel 1
Bearbeiten
Nun wollen wir die obere Grenze für den Aufwand bestimmen. Unsere Vermutung ist, dass . Nun müssen wir zeigen, dass ( siehe Definition der O-Notation). Die vereinfachte Annahme lautet . Hierbei werden keine Spezialfälle behandelt und im Induktionsschritt wird von nach n gegangen.
Induktionsvermutung:
Induktionsschritt: Wir beweisen von
zu zeigende obere Grenze:
Rekursionsgleichung einsetzen:
Induktionsvermutung einsetzen:
Somit ist der Induktionsschritt erfolgreich, wenn .
Induktionsanfang
Wir zeigen die Induktionsvermutung für einen Anfangswert, am einfachsten ist es, dies für den Rekursionsabbruch zu zeigen.
Zu zeigende obere Grenze:
Rekursionsgleichung einsetzen:
Der Induktionsanfang ist erfolgreich, wenn ist. Doch wann können wir zeigen, dass ist? Für den Wert, den wir im Induktionsanfang gezeigt haben, also für und wenn .
Beispiel 2
Bearbeiten
Nun wollen wir die obere Grenze für den Aufwand bestimmen. Unsere Vermutung ist, dass . Nun müssen wir zeigen, dass . Die vereinfachte Annahme lautet .
Induktionsvermutung:
Induktionsschritt: Wir beweisen von
Das Problem ist nun, dass wir den Induktionsschritt für positive n zeigen wollen und nicht für negative, daher müssen wir neu ansetzen.
Induktionsvermutung:
Dabei gibt es folgenden Trick: Modifiziere die Induktionsvermutung, in dem ein kleineres Polynom addiert wird.
Induktionsschritt: Wir beweisen von
Induktionsanfang für n=1
Wann können wir nun zeigen, dass ?
Für . Somit haben wir gezeigt, dass
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.2.5 zu finden.
Mastertheorem
BearbeitenAuf dieser Seite wird das Master Theorem behandelt. Die Mastermethode ist ein „Kochrezept“ zur Lösung von Rekursionsgleichungen der Form:
mit den Konstanten , f(n) ist eine asymptotische, positive Funktion, d.h.
- a steht dabei für die Anzahl der Unterprobleme.
- n/b ist die Größe eines Unterproblems
- T(n/b) ist der Aufwand zum Lösen eines Unterproblems (der Größe n/b)
- f(n) ist der Aufwand für das Zerlegen und Kombinieren in bzw. von Unterproblemen
Bei der Mastermethode handelt es sich um ein schnelles Lösungsverfahren zur Bestimmung der Laufzeitklasse einer gegebenen rekursiv definierten Funktion. Dabei gibt es 3 gängige Fälle:
- Fall 1: Obere Abschätzung
- Fall 2: Exakte Abschätzung
- Fall 3: Untere Abschätzung
Lässt sich keiner dieser 3 Fälle anwenden, so muss die Komplexität anderweitig bestimmt werden und wir müssen Voraussetzungen für die Anwendung des Mastertheorems überprüfen.
Dafür vergleicht man mit . Wir verstehen n/b als . Im Folgenden verwenden wir die verkürzte Notation .
Fall 1
BearbeitenWenn . Daraus folgt, dass f(n) polynomiell langsamer wächst als um einen Faktor . Damit haben wir die Lösung .
Fall 2
BearbeitenWenn . Daraus folgt, dass f(n) und vergleichbar schnell wachsen. Damit haben wir die Lösung .
Fall 3
BearbeitenWenn und die Regularitätsbedingung für eine Konstante und genügend große n erfüllt. Daraus folgt, dass f(n) polynomiell schneller wächst als um einen Faktor und f(n) erfüllt die sogenannte Regularitätsbedingung. Damit haben wir die Lösung .
Bedeutung
BearbeitenIn jedem Fall vergleichen wir f(n) mit . Intuitiv kann man sagen, dass die Lösung durch die größere Funktion bestimmt wird. Im zweiten Fall wachsen sie ungefähr gleich schnell. Im ersten und dritten Fall muss f(n) nicht nur kleiner oder größer als sein, sondern auch polynomiell kleiner oder größer um einen Faktor . Der dritte Fall kann nur angewandt werden, wenn die Regularitätsbedingung erfüllt ist.
Regularitätsbedingung
BearbeitenDoch wozu wird die Regularitätsbedingung benötigt? Zur Erinnerung, im dritten Fall dominiert f(n) das Wachstum von T(n). Wir müssen an dieser Stelle sicherstellen, dass auch bei rekursivem Anwenden, also wenn die Argumente kleiner werden, T(n) von f(n) dominiert wird. Veranschaulicht heißt das:
für Das Wachstum muss durch f(n) dominiert werden und darf f(n) nicht dominieren.
Die Regularitätsbedingung gilt wenn sie für f(n) und g(n) gilt auch für und auch für
Nachweis für
Voraussetzung ist, dass die Regularitätsbedingung für f(n) und g(n) gilt, d.h.:
Für gilt:
man wählt
und
Nachweis für
Voraussetzung ist, dass die Regularitätsbedingung für f(n) und g(n) gilt, d.h.:
Für gilt:
man wählt
und
Überblick
BearbeitenIst T(n) eine rekursiv definierte Funktion der Form
Dann gilt:
- 1. Fall: Wenn
- 2. Fall: Wenn
- 3. Fall: Wenn und und genügend große n dann
Idee
BearbeitenWir haben folgenden Rekursionsbaum:
Auf der ersten Ebene ist der Aufwand f(n), auf der zweiten Ebene und auf der dritten Ebene . Die Höhe des Baumes beträgt . Die Anzahl der Blätter berechnet sich durch und beträgt somit .
Fall 1: Das Gewicht wächst geometrisch von der Wurzel zu den Blättern. Die Blätter erhalten einen konstanten Anteil des Gesamtgewichts.
Fall 2: k ist 0 und das Gewicht ist ungefähr das Gleiche auf jedem der Ebenen.
Fall 3: Das Gewicht reduziert sich geometrisch von der Wurzel zu den Blättern. Die Wurzel erhält einen konstanten Anteil am Gesamtgewicht.
Beispiel 1
Bearbeiten
Fall 1:
Beispiel 2
Bearbeiten
Fall 2:
Beispiel 3
Bearbeiten
Fall 3:
und (Regularitätsbedingung)
für
Beispiel 4
Bearbeiten
Welcher Fall liegt nun vor? Das Mastertheorem kann an dieser Stelle nicht benutzt werden, da
- 1. Fall
- 2. Fall
- 3. Fall
Nützliche Hinweise
Bearbeiten- Basisumrechnung
- de L'Hospital
- Vergleiche Logarithmus vs. Polynom
Rekursionsbäume
BearbeitenAuf dieser Seite wird das Thema Rekursionsbäume behandelt. Das allgemeine Problem ist, dass man zum Abschätzen von der Aufwandsklasse einer Rekursionsgleichung gute Vermutungen braucht. Doch wie kommt man darauf? Ein Ansatz ist die Veranschaulichung durch einen Rekursionsbaum. Die Aufwandsklasse wird dann durch die Rekursionsbaummethode bestimmt. Das ist sehr nützlich, um eine Lösung zu raten, die danach durch eine andere Methode (z.B. Induktion) gezeigt wird. Rekursionsbäume sind besonders anschaulich bei Divide-and-Conquer-Algorithmen.
Spezialfall Divide and Conquer
BearbeitenBei MergeSort sehen die Divide and Conquer Schritte wie folgt aus:
- Divide: Zerteile eine Folge mit n Elementen in zwei Folgen mit je n/2 Elementen.
- Conquer: Wenn die resultierende Folge 1 oder 0 Elemente enthält,dann ist sie sortiert. Ansonsten wende MergeSort rekursiv an.
- Combine: Mische die zwei sortierten Teilfolgen.
public List mergeSort(List f) {
if (f.size() <= 1) {
return f;
} else {
int m = f.size() / 2;
List left = mergeSort(f.subList(0,m));
List right = mergeSort(f.subList(m,f.size());
return merge(left, right);
}
}
Rekursionsbaum
BearbeitenHerleitung des Aufwandes
BearbeitenDie Grundidee ist das wiederholte Einsetzen der Rekursionsgleichung in sich selbst als Baum dargestellt. Das Ziel ist ein Muster zu erkennen. Bei einem Rekursionsbaum beschreibt ein Knoten die Kosten eines Teilproblems. Die Blätter sind die Kosten der Basis fällt T(0) und T(1). Der Aufwand bestimmt sich aus der Summe über alle Ebenen.
1. Ebene
2. Ebene
3. Ebene
....
n. Ebene
Der Aufwand berechnet sich nun wie folgt:
Allgemein bestimmt sich der Aufwand T(n) durch die Summe des Aufwands je Ebene und des Aufwands der Blattebene.
Bezogen auf den gegebenen Rekursionsbaum wäre das
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8.3 zu finden.
Entwurfsprinzipien
BearbeitenAuf dieser Seite werden wir und mit Entwurfsprinzipien und einer Einführung in die Entwurfsmuster beschäftigen. Die Ableitung eines optimalen Algorithmus aus Anforderungsbeschreibungen ist nicht automatisierbar. Der Algorithmenentwurf ist eine kreative Tätigkeit, die durch Muster ( best practices) unterstützt wird. Vergleichbar ist das mit Mustern von Gebäuden in der Architektur oder mit Mustern aus der Softwarearchitektur.
Schrittweise Verfeinerung
BearbeitenDer Entwurf von Algorithmen erfolgt nach dem Prinzip der schrittweisen Verfeinerung von Pseudo Code Algorithmen. Pseudo Code Teile werden im ersten Schritt durch verfeinerten Pseudo Code ersetzt und im nächsten Schritt durch Programmiersprachen Code.
Beispiel 1
Bearbeiten1. Pellkartoffeln kochen
verfeinert zu :
1.1 Fülle Topf mit Kartoffeln
1.2 Füge Wasser dazu
1.3 Stelle topf auf Herdplatte
1.4 Stelle Drehknopf auf 7
1.5 Koche das Wasser
Beispiel 2
BearbeitenWir benutzen die Fakultät als Prozeduraufruf
Factorial(n)
Nun schreiben wir die Fakultät als Algorithmus
Fac: var X;Y:int; input X; Y:=1; while X>1 do Y:=Y*X; X:= X-1 od output Y
Nun schreiben wir die Fakultät als Implementierungscode
public static int factorial (int x) {
...
}
Einsatz von Algorithmenmustern
BearbeitenDie Idee ist, dass generische Algorithmenmuster für bestimmte Problemklassen an eine konkrete Aufgabe angepasst werden. Das Lösungsverfahrens wird am Beispiel eines einfachen Vertreters der Problemklasse dokumentiert. Es wird eine Bibliothek von Mustern (Design Pattern) zur Ableitung eines abstrakten Programmrahmens benutzt. Durch parametrisierte Algorithmen und Vererbung wird die Programmiersprache unterstützt.
Greedyalgorithmus
BearbeitenAuf dieser Seite wird der Greedyalgorithmus behandelt.
Greedy bedeutet "gierig". Der Algorithmus erfolgt nach dem Prinzip, dass versucht wird mit jedem Teilschritt so viel wie möglich zu erreichen. Greedy-Algorithmen (gierige Algorithmen) zeichnen sich dadurch aus, dass sie immer denjenigen Folgezustand auswählen, der zum Zeitpunkt der Wahl den größten Gewinn bzw. das beste Ergebnis verspricht.
Lokales Optimum
BearbeitenDer Greedy Algorithmus berechnet in jedem Schritt das lokale Optimum, dabei kann jedoch das globale Optimum verfehlt werden.
Jedoch entspricht in vielen Fällen das lokale Optimum auch dem globalem Optimum, bzw. es reicht ein lokales Optimum aus.
Problemklasse
Bearbeiten- Gegebene Menge von Eingabewerten
- Menge von Lösungen, die aus Eingabewerten aufgebaut sind
- Lösungen lassen sich schrittweise aus partiellen Lösungen, beginnend bei der leeren Lösung, durch Hinzunahme von Eingabewerten aufbauen. Alternativ: bei einer ganzen Menge beginnend schrittweise jeweils ein Element wegnehmen
- Bewertungsfunktion für partielle und vollständige Lösungen
- Gesucht wird die/eine optimale Lösung
Das Münzwechselproblem
BearbeitenAuf dieser Seite wird das Münzwechselproblem NICHT behandelt.
Beispiel
BearbeitenAls Beispiel nehmen wir die Herausgabe von Wechselgeld auf Beträge unter 1€. Verfügbar sind die Münzen mit den Werten 50ct, 10ct, 5ct, 2ct, 1ct. Unser Ziel ist, so wenig Münzen wie möglich in das Portemonnaie zu bekommen.
Ein Beispiel:
Es wird jeweils immer die größte Münze unter dem Zielwert genommen und von diesem abgezogen. Das wird so lange durchgeführt, bis der Zielwert Null ist.
Formalisierung
BearbeitenGesucht ist ein Algorithmus der folgende Eigenschaften beschreibt.
Bei der Eingabe muss gelten
- 1. dass die eingegebene Zahl eine natürliche Zahl ist, also
- 2. dass eine Menge von Münzwerten zur Verfügung steht
Die Ausgabe besteht dann aus ganzen Zahlen . Dabei ist die Anzahl der Münzen des Münzwertes für für und haben die Eigenschaften
- 1.
- 2. ist minimal unter allen Lösungen für 1.
Algorithmus
Bearbeiten- 1. Nehme jeweils immer die größte Münze unter dem Zielwert und ziehe sie von diesem ab.
- 2. Verfahre derart, bis der Zielwert gleich Null ist.
Der dazugehörige Code in Java:
public int[] moneyChange(int[] currency, int amount){
int[] change = new int[currency.length];
int currentCoin = currency.length-1;
while(amount > 0){
while(amount < currency[currentCoin] && currentCoin > 0)
currentCoin--;
if(amount >= currency[currentCoin] && currentCoin >= 0){
amount -= currency[currentCoin];
change[currentCoin]++;
} else return null;
}
return change;
}
Die Methode moneyChange wird dabei aufgerufen durch:
int[] currency = {1,2,5,10,20,50};
int amount = 78;
int[] change = moneyChange(currency, amount);
Lokales Optimum
BearbeitenDer Greedy Algorithmus berechnet im jedem Schritt das lokale Optimum, dabei kann jedoch das globale Optimum verfehlt werden.
Beispiel: Münzen 11ct, 5ct und 1ct. Unser Zielwert ist 15ct. Nach Greedy benutzen wir 11+1+1+1+1, das Optimum wäre aber 5+5+5.
Analyse
BearbeitenTheorem
BearbeitenFür endlicher Länge und mit endlichen positiven Werten und endlichem positivem , terminiert der Algorithmus moneyChange nach endlich viele Schritten.
Beweis
Bearbeiten- In Zeile 03 wird mit einem endlichen positiven Wert initialisiert
- In Zeile 05 und 06 wird nur dekrementiert, spätestens beim Wert 0 wird die Schleife beendet (also eine endliche Wiederholung)
- Falls die Zeilen 08 und 09 nicht ausgeführt werden, endet die Berechnung direkt in 10; andernfalls wird in Zeile 08 echt kleiner
- Irgendwann ist also der Bedingung in Zeile 04 nicht mehr gegeben und die Berechnung terminiert
Theorem
BearbeitenFür Eingabe mit und hat der Algorithmus moneyChange eine Laufzeit von O(m+n).
Beweis
Bearbeiten- Die Zeile 6 wird maximal m-mal ausgeführt
- Die Zeile 8 wird maximal n-mal ausgeführt, falls es nur eine Münze mit dem Wert "1" gibt
Theorem
BearbeitenDer Algorithmus moneyChange löst für das Münzwechselproblem.
Beweis
BearbeitenBei der Lösung musste zum Einen gelten, dass ist. Da der Wert stets um den Wert einer Münze verringert wird, während um eins inkrementiert wird, ist dies erfüllt.
Die zweite Aussage zur Lösung war, dass minimal unter allen Lösungen sein soll. Dies wird hier nur für Münzen vom Wert 1,2 und 5 betrachtet, wobei es für die Münzen 10, 20 und 50 analog zu beweisen ist.
Zunächst gilt, dass 2er-Münzen stets 1er-Münzen zu bevorzugen sind, da es keinen Sinn macht im Algorithmus auf eine 2er-Münze zu verzichten, um dann im nächsten Schritt mehr 1er-Münzen zu bekommen. Das bedeutet, dass eine optimale Lösung maximal eine 1er-Münze beinhaltet.
Weiterhin gilt, eine optimale Lösung hat nicht mehr als zwei 2er-Münzen. Sollten drei 2er-Münzen in der Lösung sein, ist es besser diese durch eine 1er und eine 5er-Münze zu ersetzen.
Des Weiteren gilt, eine optimale Lösung kann nicht gleichzeitig eine 1er-Münze und zwei 2er-Münzen enthalten, weil dies durch eine 5er-Münze dargestellt werden kann.
Es folgt, dass der durch 1er- und 2er-Münzen dargestellte Betrag nicht mehr als 4 sein kann. Also ist eine maximale Wahl von 5er-Münzen im Greedy-Verfahren optimal.
Divide and Conquer
BearbeitenAuf dieser Seite wird Divide and Conquer behandelt. Divide and Conquer bedeutet "Teile und Herrsche". Quick Sort und Merge Sort sind typische Vertreter. Es verfolgt das Prinzip, dass auf identische Probleme mit einer kleinen Eingabemenge eine rekursive Rückführung geschieht.
Grundidee
BearbeitenTeile das gegebene Problem in mehrere getrennte Teilprobleme auf, löse diese einzeln und setze die Lösungen des ursprünglichen Problems aus den Teillösungen zusammen. Wende dieselbe Technik auf jedes der Teilprobleme an, dann auf deren Teilprobleme, usw, bis die Teilprobleme klein genug sind, dass man eine Lösung explizit angeben kann. Strebe an, dass jedes Teilproblem von derselben Art ist wie das ursprüngliche Problem, so dass es mit demselben Algorithmus gelöst werden kann.
Muster
Bearbeitenprocedure DIVANDCONQ (P: problem)
begin
…
if [P klein ]
then [explizite Lösung ]
else [ Teile P auf in P1, …, Pk ];
DIVANDCONQ (P1 ) ;
… ;
DIVANDCONQ (Pk) ;
[ Setze Lösung für P aus Lösungen für P1, …, Pk zusammen ]
fi
end
Beispiel
BearbeitenWir nehmen als Beispiel die Spielpläne für Turniere. Gegeben sind Spieler, wobei k ganzzahlig und größer 0 ist. Des weiteren sind mindestens n-1 Turniertage gegeben und jeder Spieler spielt gegen jeden anderen. Der Turnierplan ist bekannt und die Aufgabe ist für zu konstruieren (Rekursionsprinzip).
Spielplan für
| Tag 1 | Tag 2 | Tag 3 | |
| Spieler 1 | 2 | 3 | 4 |
| Spieler 2 | 1 | 4 | 3 |
| Spieler 3 | 4 | 1 | 2 |
| Spieler 4 | 3 | 2 | 1 |
Spielplan für
Für kleine Problemgröße kann Lösung direkt angegeben werden:
| Tag 1 | |
| Spieler 1 | 2 |
| Spieler 2 | 1 |
Nun konstruieren wir aus .
| Tag 1...n-1 | Tag n...m-1 | |
| Spieler 1... | ||
| n+1... |
- mit jeweils um n erhöhten Elementen
- Matrix, konstruiert durch zyklisches Verschieben der Spalte (n+1,…,m) für
- Matrix, konstruiert durch zyklisches Verschieben der Zeile (1,2,..., n)
Spielplan für
| Tag 1 | Tag 2 | Tag 3 | Tag 4 | Tag 5 | Tag 6 | Tag 7 | |
| Spieler 1 | 2 | 3 | 4 | 5 | 8 | 7 | 6 |
| Spieler 2 | 1 | 4 | 3 | 6 | 5 | 8 | 7 |
| Spieler 3 | 4 | 1 | 2 | 7 | 6 | 5 | 8 |
| Spieler 4 | 3 | 2 | 1 | 8 | 7 | 6 | 5 |
| Spieler 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 |
| Spieler 6 | 5 | 8 | 7 | 2 | 3 | 4 | 1 |
| Spieler 7 | 8 | 5 | 6 | 3 | 4 | 1 | 2 |
| Spieler 8 | 7 | 6 | 5 | 4 | 1 | 2 | 3 |
Spieler 1-4 Tag 1-3
Spieler 1-4 Tag 4-7
Spieler 5-8 Tag 1-3
Spieler 5-8 Tag 4-7
Türme von Hanoi
BearbeitenBei den Türmen von Hanoi sind 3 Stapel mit Scheiben unterschiedlicher Größe gegeben. In jedem Schritt darf eine Scheibe, die ganz oben auf einem Stapel liegt, auf einen anderen Stapel gelegt werden. Allerdings unter der Bedingung, dass sie nur auf eine kleinere Scheibe gelegt werden darf.
Das Ziel ist es alle Scheiben vom ganz linken Stapel auf den ganz rechten Stapel zu verschieben.
Illegale Spielzüge sind dabei, wenn eine größere Scheibe auf eine kleinere Scheibe gelegt wird.
Algorithmenentwurf
BearbeitenReduziere das Problem n Scheiben zu verschieben darauf nur noch n-1 Scheiben zu verschieben, bis schlussendlich nur noch eine Scheibe übrig bleibt.
Dies ist ein ähnliches Prinzip wie bei Induktionsbeweisen. Dabei kann das Nutzen des Algorithmus für n-1 Scheiben als der Induktionsschritt gesehen werden. Der Basisfall, also der Induktionsanfang, ist dabei, wenn es nur eine Scheibe gibt.
Um die Aufgabe zu lösen, muss beim Verschieben von mehr als einer Scheibe der dritte Stapel immer als "Zwischenlager" genutzt werden. Welcher der drei Stapel das "Zwischenlager" ist, kann ja nach Schritt wechseln. In dem Beispiel bei 5 Scheiben auf dem linken Stapel(A), dient dieser als Startstapel und soll auf den linken Stapel(C), also auf den Zielstapel, verschoben werden. Im ersten Schritt dient der mittlere Stapel(B) somit als Zwischenlager.
Das erste Unterziel ist es die obersten vier Scheiben von A zu verschieben. Dafür dient A als Startstapel, B als Zielstapel und C als Zwischenlager.
Weiterhin muss gewährleistet sein, dass das Zwischenlager nach Abschluss wieder genauso aussieht wie zuvor.
Der Pseudocode sieht wie folgt aus:
Algorithmus hanoi
Eingabe:
Startstapel S,
Zielstapel Z,
Zwischenlager L,
Anzahl der Scheiben n
Ausgabe:
Aktionenfolgen um alle Scheiben von S nach L zu verschieben
Falls n=1
Entferne die oberste Scheibe k von S und füge sie Z hinzu
Gib aus "Verschiebe k von S nach Z"
Ansonsten
hanoi(S,L,Z,n-1);
Entferne die oberste Scheibe k von S und füge sie Z hinzu
Gib aus "Verschiebe k von S nach Z"
hanoi(L,Z,S,n-1);
Für die Implementierung in Java wird als Repräsentation der Stapel je ein und für eine Scheibe je ein verwendet. Bei den Scheiben gibt der Wert jeweils die Größe der Scheibe an.
public void hanoi(Stack<Integer> start, Stack<Integer> goal, Stack<Integer> tmp, int numDiscs){
if(numDiscs == 1){
int disc = start.pop();
goal.push(disc);
System.out.println("Moving disc " + disc);
}else{
hanoi(start, tmp, goal, numDiscs-1);
int disc = start.pop();
goal.push(disc);
System.out.println("Moving disc " + disc);
hanoi(tmp, goal, start, numDiscs-1);
}
}
Der Aufruf erfolgt durch:
Stack<Integer> start = new Stack<Integer>();
for(int i = 5; i > 0; i--) start.push(i);
hanoi(start, new Stack<Integer>(), new Stack<Integer>(), 5);
Analyse
BearbeitenTheorem
Der Algorithmus terminiert nach endlich vielen Schritten, wenn die Anzahl der Scheiben positiv ist.
Beweis
- Die Zeile 03 stellt das Rekursionsende da und der Algorithmus terminiert bei numDiscs = 1
- Die Else-Bedingung führt dazu, dass durch die rekursiven Aufrufe der Wert von numDiscs sich immer um 1 verringert.
Theorem
Für n Schreiben hat der Algortihmus eine Laufzeit von .
Beweis
Die Rekursionsgleichung für ist:
Der Beweis erfolgt damit durch Induktion.
Theorem
Der Algorithmus löst das Problem der Türme von Hanoi.
Beweis
Zu zeigen gelten:
- Der Algorithmus hält sich an die Spielregeln, dass in jedem Zug nur eine Scheibe von oben von einem Stapel entfernt werden darf und auf einen leeren Stapel oder auf eine größere Scheibe gelegt wird.
- Bei der Terminierung sind alle Scheiben auf dem Zielstapel.
Beide Aussagen kann man durch Induktion nach der Anzahl der Scheiben n beweisen.
Für : hier wird eine Scheibe direkt vom Startstapel zum leeren Zielstapel verschoben. In diesem Fall sind beide Bedingungen erfüllt.
Für : Es sind n Scheiben von Stapel A zu C zu verschieben. Dazu sei B der dritte Stapel. Zunächst wird der Algorithmus rekursiv für die obersten n-1 Scheiben mit Zielstapel B aufgerufen. Da alle diese n-1 Scheiben kleiner als die unterste Scheibe ist und diese nicht bewegt wird, ist dies das gleiche Problem, als wenn die unterste Scheibe gar nicht da wäre. Nach rekursiven Aufruf werden also die n-1 Scheiben legal nach B verschoben. C ist dabei anschließend wieder leer. Die Verschiebung der untersten Scheibe nach C ist legal. Die rekursive Verschiebung der auf B liegenden n-1 Scheiben nach C ist nun wieder legal, aufgrund der Tatsache, dass auf C nur eine größere Scheibe liegt.
Der Algorithmus ist ebenso optimal, das heißt, er findet eine minimale Anzahl von Zügen zur Lösung des Problems.
Weiterhin ist eine Animation des Algorithmus verfügbar.
Backtracking
BearbeitenAuf dieser Seite wird das Backtracking behandelt.
Die Idee des Backtracking ist das Versuchs-und-Irrtum-Prinzip (trial and error). Versuche, die erreichte Teillösung schrittweise zu einer Gesamtlösung auszubauen. Falls die Teillösung nicht zu einer Lösung führen kann, dann nimm den letzten Schritt bzw. die letzten Schritte zurück und probiere stattdessen alternative Wege.Alle in Frage kommenden Lösungswege werden ausprobiert. Vorhandene Lösung wird entweder gefunden (unter Umständen nach sehr langer Laufzeit) oder es existiert definitiv keine Lösung. Backtracking (“Zurückverfolgen“) ist eine allgemeine systematische Suchtechnik. KF ist die Menge von Konfigurationen. ist die Anfangskonfiguration. Für jede Konfiguration gibt es eine direkte Erweiterung . Außerdem ist für jede Konfiguration entscheidbar, ob sie eine Lösung ist. Aufgerufen wird Backtracking mit .
Labyrinth Suche
Bearbeiten
Backtracking Muster
Bearbeitenprocedure BACKTRACK (K: Konfiguration)
begin
…
if [ K ist Lösung ]
then [ gib K aus ]
else
for each [ jede direkte Erweiterung K0 von K ]
do
BACKTRACK (K0)
od
fi
end
Einsatzfelder
BearbeitenZu den typischen Einsatzfeldern von Backtracking gehören zum Beispiel einige Spielprogramme (Schach, Dame, Labyrinthsuche,…). Aber auch die Erfüllbarkeit von logischen Aussagen wie logische Programmiersprachen, Optimierung von Gattern oder Model checking (Theorembeweiser). Ein weiteres Einsatzfeld sind Planungsprobleme und Konfigurationen wie logistische Fragestellungen (Traveling Salesman, der kürzeste Wege, die optimale Verteilung, das Färben von Landkarten oder auch nichtdeterministisch-lösbare Probleme.
Beispiel Acht Damen Problem
Bearbeiten
Gesucht sind alle Konfigurationen von 8 Damen auf einem 8 x 8-Schachbrett, so dass keine Dame eine andere bedroht. Gesucht ist nun ein geeignetes KF. Für jede Lösungskonfigurationen L mit gelten . Für jedes ist leicht entscheidbar, ob . Die Konfigurationen lassen sich schrittweise erweitern und wir erhalten eine hierarchische Struktur. Es sollte auch beachtet werden, dass KF nicht zu groß sein sollte.
: Es sind 8 Damen auf dem Brett
: Keine zwei Damen bedrohen sich.
KF wird so gewählt, dass die Konfiguration mit je einer Dame in den ersten n Zeilen, , so dass diese sich nicht bedrohen.

Diese Konfiguration ist nun nicht mehr erweiterbar. Jedes Feld in Zeile 7 ist bereits bedroht.
procedure PLATZIERE (i:[1..8]);
begin
var h: [1..8];
for h:=1 to 8 do
if [Feld in Zeile i, Spalte h nicht bedroht]
then
[Setze Dame auf dieses Feld (i,h)];
if [Brett voll] /* i=8*/
then [Gib Konfiguration aus ]
else PLATZIERE (i+1)
fi
fi
od
end

Die Array Repräsentation ist [4,1,3,5,0,0,0,0]. Die Diagonalen sind belegt wenn:
i+h = i+h
i-h = i-h
(i = Spalte, h = Zeile)
Die Zeilen snd belegt, wenn die Position im Array besetzt ist und die Spalten sind belegt, wenn die Nummer im Array existiert.
Der initiale Aufruf geschieht mir Platziere(1). Es gibt insgesamt 92 Lösungen. Die Konfigurationen ist etwa als zweidimensionales boolesches Array oder als eindimensionales Array mit einer Damenposition pro Zeile realisierbar. Redundante Informationen über bedrohte Spalten und Diagonalen bieten Optimierungspotential.
Algorithmus in Java
BearbeitenDer Code zu dem Problem im allgemeinen Fall sieht in Java wie folgt aus.
public boolean isValid(int[] board, int current, int place){
for(int i = 0; i < current-1; i++){
if(board[i] == place) return false;
if(place+current == board[i] + (i+1)) return false;
if(place-current == board[i] - (i+1)) return false;
}
return true;
}
public int[] placeQueen(int[] board, int current){
int[] tmp;
for(int i=0; i< board.length; i++){
if(isValid(board, current, i)){
board[current-1] = i;
if(current == board.length) return board;
else{
tmp = placeQueen(board, current+1);
if(tmp != null) return tmp;
}
}
}
return null;
}
Aufgerufen wird der Code durch:
int[] result = placeQueen(new int[8], 1);
Analyse
BearbeitenTheorem
Der Algorithmus terminiert nach endlich vielen Schritten, wenn die Anzahl der Felder positiv ist.
Beweis
Die Methode terminiert offensichtlich immer.
In wird rekursiv stets um einen erhöhten Parameter aufgerufen. Die for-Schleife hat auch stets eine konstante Zahl an Durchgängen.
Theorem
Für ein Feld der Größe n x n hat der Algorithmus eine Laufzeit von .
Beweis
Im schlimmsten Fall werden alle Konfigurationen betrachtet:
- n Positionen für eine einzelne Dame
- n Damen sind zu plazieren
Die tatsächliche Laufzeit ist weitaus geringer, da viele Konfigurationen schon früh als nicht-erweiterbar erkannt werden. Dennoch ist die Laufzeit im schlimmsten Fall exponentiell .
Theorem
Der Algorithmus löst das n-Damenproblem.
Dynamische Programmierung
BearbeitenAuf dieser Seite wird die dynamische Programmierung behandelt.
Die dynamische Programmierung vereint die Ideen verschiedener Muster. Zum einen die Wahl der optimalen Teillösung des Greedy Musters und zum anderen die Rekursion und den Konfigurationsbaum aus Divide and Conquer und Backtracking. Die Unterschiede sind, dass Divide and Conquer unabhängige Teilprobleme löst und in der dynamischen Programmierung eine Optimierung von abhängigen Teilproblemen durchgeführt wird. Die dynamische Programmierung ist eine „bottom-up“-Realisierung der Backtracking-Strategie. Die Anwendungsbereiche sind die selben wie bei Greedy, jedoch wird dynamische Programmierung insbesondere dort angewandt, wo Greedy nur suboptimale Lösungen liefert.
Idee
BearbeitenBei der dynamischen Programmierung werden kleinere Teilprobleme zuerst gelöst, um aus diesen größere Teillösungen zusammenzusetzen. Das Problemlösen geschieht quasi auf Vorrat. Es werden möglichst nur die Teilprobleme gelöst, die bei der Lösung der großen Probleme auch tatsächlich benötigt werden. Wir erzielen einen Gewinn, wenn identische Teilprobleme in mehreren Lösungszweigen betrachtet werden. Rekursives Problemlösen wird ersetzt durch Iteration und abgespeicherte Teilergebnisse.
Nicht immer ist es überhaupt möglich, die Lösungen kleinerer Probleme so zu kombinieren, dass sich die Lösung eines größeren Problems ergibt. Die Anzahl der zu lösenden Probleme kann unvertretbar groß werden. Es können zu viele Teillösungen entstehen, die dann doch nicht benötigt werden oder der Gewinn der Wiederverwendung ist zu gering, da die Lösungszweige disjunkt sind.
Beispiel Editierdistanz
BearbeitenGegeben sind zwei Zeichenketten s und t, was ist die minimale Anzahl an Einfüge-, Lösch- und Ersetzoperationen um s in t zu transformieren?
Als Beispiel entspricht s "Haus" und t "Maus". Die Lösung ist hier, dass "H" durch "M" ersetzt wird. Bei s= "Katze" und t="Glatze" wird "K" durch "G" ersetzt und "I" hinzugefügt. Die Editierdistanz kommt in der Rechtschreibprüfung und Plagiatserkennung zur Anwendung.
Formalisierung
BearbeitenDefinition ( Ein-Schritt Modifikation)
Beachte
- Jedes (für )
- Jedes (für )
- Jedes (für )
heißt Ein-Schritt Modifikation von s.
Definition (k-Schritt Modifikation) Eine Zeichenkette t heißt k-Schritt Modifikation von s, wenn es Zeichenketten u gibt mit:
- u ist eine Ein-Schritt Modifikation von s
- t ist eine k-1-Schritt Modifikation von u
Definition (Editierdistanz, auch Levenshtein-Distanz)
Ist s eine d-Schritt Modifikation von t, so ist auch s eine d+2j Modifikation von t für jedes j>0.Eine minimale Modifikation muss nicht eindeutig sein. Wir sind aber hier nur an dem Wert einer minimalen Modifikation interessiert.
Charakterisierung und Algorithmus
BearbeitenDie Idee ist, dass die Berechnung von D(s,t) auf die Berechnung von D auf die Präfixe von s und t zurückgeführt wird.
Definition
Sei
Definiere
Beachte für z.B i=0 haben wir (leerer String).
Wir beobachten, dass gilt . Dies ist nun zu berechnen. Zudem ist , also sind zwei leere Strings identisch.
für j=1,..,n. Also alle Zeichen müssen eingefügt werden.
für i=1,...,m. Also alle Zeichen müssen eingefügt werden.
Theorem der zentralen Charakterisierung der Editierdistanz
BearbeitenFalls .
Ansonsten:
Algorithmus
BearbeitenFor j=0,...,n set (s,t)=j For i=0,...,m set (s,t)=i For i=1,..,m For j=1,...,n If set else min {} Return
Analyse
BearbeitenTheorem
Für endliche Zeichenketten s und t terminiert der Algorithmus editdistance nach endlich vielen Schritten.
Beweis
Der Beweis folgt auf dem nächsten Theorem.
Theorem
Für die Eingaben und hat der Algorithmus eine Laufzeit von .
Beweis
Der Beweis besteht aus einer einfachen Schleifenanalyse.
Theorem
Der Algorithmus editdistance berechnet die Editierdistanz zweier Zeichenketten s und t.
Beweis
Der Beweis folgt direkt aus der zentralen Charakterisierung der Editierdistanz.
Einleitung Suchen
BearbeitenIn diesem Kapitel geben wir einen Überblick über das Thema Suchen. Suchprobleme sind eine der häufigsten Probleme in der Informatik. Man kann in sortierten Folgen suchen, Zeichenketten im Text suchen, Dokumente in Textkorpora suchen, oder allgemeine Lösungen von Problemräumen, wie der Spielbaumsuche oder der Plansuche, suchen. Hier behandeln wir zunächst die Suche in sortierten Folgen.
Motivation
BearbeitenBeim Suchen wiederholt man häufig sehr nützliche Beispielalgorithmen, oder lernt diese sogar neu kennen. Außerdem dient es der Vorbereitung der theoretischen Betrachtungen zur Komplexität von Algorithmen. Des Weiteren dient es der informellen Diskussion von Entwurfsentscheidungen.
Suchen in sortierten Folgen
Bearbeiten- Annahme:
- Die Folge F ist ein Feld mit numerischen Werten. Dazu ist die Folge sortiert, das heißt, wenn i<j, dann ist F[i]<F[j]. Auf das i-te Element hat man Zugriff über F[i]. Es wird nur der Suchschlüssel berücksichtigt.
Ein Beispiel ist ein Telefonbuch, in dem wir nach Namen suchen möchten. Doch wie repräsentiert man diese Daten?
Einschub lineare Datenstrukturen
BearbeitenDefinition
BearbeitenEine lineare Datenstruktur L ist eine Sequenz . Die lineare Datenstruktur ordnet Elemente (entweder primitive Datentypen oder komplexere Datenstrukturen) in einer linearen Anordnung an.
Beispiel
BearbeitenZahlenfolgen
| 5 | 4 | 6 | 1 | 3 | 2 |
Strings
| L | I | N | E | A | R |
Atomare Operationen
BearbeitenZu den Operationen gehören Lesen mit
- get(i): Element an Position i lesen
- first(): erstes Element lesen
- last(): letztes Element lesen
- next(e): Element nach Element e lesen
und Schreiben mit
- set(i,e): Element an Position i auf e setzen
- add(i,e): Element e an Position i einfügen
- del(i): Element an Position i löschen
Arrays und Listen
BearbeitenEs gibt zwei Möglichkeiten lineare Datenstrukturen zu realisieren. Entweder Arrays oder (verlinkte) Listen. Arrays belegen einen zusammenhängenden Bereich im Speicher. Elemente einer verlinkten Liste können beliebig verteilt sein. Ob zur Realisierung einer linearen Datenstruktur ein Array oder eine Liste verwendet wird, hängt von der Anwendung ab. Arrays werden meist für statische Datenstrukturen verwendet, d.h. wenn die Länge des Arrays nicht verändert wird. Listen werden meist für dynamische Datenstrukturen verwendet, d.h. wenn die Länge variabel ist. Zu den positiven Eigenschaften von Arrays zählen der schneller Zugriff auf Einzelelemente durch den Index. Zu den negativen Eigenschaften von Arrays zählen das sehr aufwändige Einfügen der Elemente. Zu den positiven Eigenschaften von Listen zählen die relativ effiziente Manipulation, zu den negativen Eigenschaften der ineffiziente Direktzugriff.
Einfache verlinkte Liste von Zahlen in Java
Bearbeitenpublic class IntegerList {
private class IntegerListElement{
int value;
IntegerListElement next;
}
IntegerListElement first;
int size = 0;
private IntegerListElement getElement(int i){
if(i+1 > size)
throw new IllegalArgumentException();
int idx = 0;
IntegerListElement current = first;
while(idx != i){
current = current.next;
idx ++;
}
return current;
}
public int get(int i){
return this.getElement(i).value;
}
public int add(int pos, int val){
IntegerListElement newElem = new IntegerListElement();
newElem.value = val;
if(pos > 0){
IntegerListElement e = this.getElement(pos‐1);
newElem.next = e.next;
e.next = newElem;
}else{
newElem.next = this.first;
this.first = newElem;
}
Suchen und Sortieren
BearbeitenSuchen und Sortieren sind voneinander abhängige Operationen. Dabei gibt es zwei Ansätze: Wenn Elemente nie sortiert sind, dann ist die Suche sehr aufwändig. Wenn die Elemente sortiert sind, wird die Suche erleichtert, jedoch kann das Sortieren an sich sehr aufwändig sein. Wenn Elemente hinzugefügt oder gelöscht werden ist diese Problematik noch sichtbarer. Nur ein unsortiertes Element macht die Suche aufwändig, doch bei jeder Einfügung oder Löschung zu sortieren ist ebenfalls sehr aufwändig. Spezielle dynamische Datenstrukturen erlauben eine automatische und effiziente Sortierung bei Einfügung oder Löschung. lol ist alles falsch ich bin ncool und ihr seid alle behindert
Lineare Datenstruktur in Java
Bearbeiten- Arrays:
- int[] arr = new int[10];
- arr[1] = 4;
- Listen:
- List<Integer> myList = new LinkedList<Integer>();
- myList.add(5);
- Neben LinkedList unterstützt Java eine Reihe weiterer Listenimplementierungen mit unterschiedlichen Vor- und Nachteilen
- Schnittstelle List<Type> beinhaltet die gemeinsamen Methoden
Suche
Bearbeiten- Problembeschreibung
- Die Eingabe ist eine Folge F mit n Elementen von Zahlen und Suchelementen k. Die Ausgabe ist eine erfolgreiche oder nicht erfolgreiche Suche. Erfolgreich ist sie, wenn der Index p ist. Eventuell muss man festlegen, was bei Mehrfachvorkommen passiert. Normalerweise gilt dann das erste Vorkommen. Ist die Suche nicht erfolgreich, dann ist die Ausgabe -1.
- Merkmale der Suche
- Es gibt immer einen Suchschlüssel für Suchelemente, z.B. Zahlen. Außerdem ist eine Suche immer erfolgreich oder erfolglos. Die Suche basiert auf Vergleichsoperationen und die Daten sind zunächst als Feld, bzw. Array, oder Liste dargestellt.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5 zu finden.
Sequentielle Suche
BearbeitenDieses Kapitel handelt von der sequentiellen Suche. Die Idee dieses Suchalgorithmus ist, dass zuerst das erste Elemente der Liste mit dem gesuchten Elemente verglichen wird, wenn sie übereinstimmen wird der aktuelle Index zurückgegeben. Wenn nicht wird der Schritt mit dem nächsten Element wiederholt. Sollte das gesuchte Element bis zum Ende der Folge nicht gefunden werden, war die Suche erfolglos und -1 wird zurückgegeben.
Algorithmus
Bearbeiten
int SeqSearch(int[] F, int k) {
/ * output: Position p (0 ≤ p ≤ n-1) */
}
int n = F.length;
for (int i = 0; i < n; i++) {
if (F[i] == k) {
return i;
}
return -1; }
Dabei ist Int[] die sortierte Folge von int, int k der Suchschlüssel und die Folge F hat die Länge n.
Aufwands Analyse
BearbeitenDas Terminierungs-Theorem besagt, dass der Algorithmus SeqSearch für eine endliche Eingabe nach endlicher Zeit terminiert. Das Korrektheits-Theorem besagt, falls das Array F ein Element k enthält, gibt SeqSearch(F,k) den Indes des ersten Vorkommens von k zurück. Ansonsten gibt SeqSearch(F,k) den Wert -1 zurück Im besten Fall beträgt die Anzahl der Vergleiche 1, das heißt direkt bei dem ersten Suchdurchlauf wird der Suchschlüssel gefunden. Im schlechtesten Fall beträgt die Anzahl der Vergleiche n, das heißt im letzten Suchdurchlauf wird der Suchschlüssel gefunden. Der Durchschnitt bei einer erfolgreichen Suche beträgt (n+1)/2 und der Durchschnitt einer erfolglosen Suche n. Die Folgen müssen nicht sortiert sein. Der Algorithmus SeqSearch hat also eine Worst-Case Laufzeit von .
Sequentielle Suche in Java
Bearbeiten
public class SequentialSearch{
public final static int NO_KEY = -1;
static int SeqSearch(int[] F, int k) {
for (int i = 0; i < F.length; i++)
if (F[i] == k)
return i;
return NO_KEY;
}
public static void main(String[ ] args){
if (args.length != 1) {
System.out.println(''usage: SequentialSearch
<key>'');
return;
}
int[ ] f = {2, 4, 5, 6, 7, 8, 9, 11};
int k = Integer.parseInt(args[0]);
System.out.println(''Sequentiell:“+seqSearch(f,k));
}
}
In der Klasse SeqSearch ist eine Konstante NO_KEY definiert, die als Ergebnis zurückgegeben wird, wenn der gesuchte Wert nicht im Feld gefunden wurde. Die Methode search wird schließlich in der Klassenmethode main aufgerufen, um das Feld f nach dem Schlüsselwert k zu durchsuchen. Dieser Wert ist als Parameter beim Programmaufruf anzugeben. Da die Programmparameter als Feld args von Zeichenketten übergeben werden, ist zuvor noch eine Konvertierung in einen int-Wert mit Hilfe der Methode parseInt der Klasse java.lang.Integer vorzunehmen. Somit bedeutet der Programmaufruf "java SeqSearch 4" die Suche nach dem Wert 4 in der gegebenen Folge. Der Aufruf erfolgt mit java SequentialSearch 4
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.1.1 zu finden.
Binäre Suche
BearbeitenDieses Kapitel behandelt die binäre Suche. Wir stellen uns die Frage, wie die Suche effizienter werden könnte. Das Prinzip der binären Suche ist zuerst den mittleren Eintrag zu wählen und zu prüfen ob sich der gesuchte Wert in der linken oder rechten Hälfte der Liste befindet. Anschließend fährt man rekursiv mit der Hälfte fort, in der sich der Eintrag befindet. Voraussetzung für das binäre Suchverfahren ist, dass die Folge sortiert ist. Das Suchverfahren entspricht dem Entwurfsmuster von Divide-and-Conquer.
Beispiel
BearbeitenRekursiver Algorithmus
Bearbeitenint BinarySearch(int[] F, int k){
/*input: Folge F der Länge n, Schlüssel k */
/*output: Position p */
return BinarySearchRec(F, k, 0, F.length-1); //initialer Aufruf
}
int BinarySearchRec (int[] F, int k, int u, int o) {
/* input: Folge F der Länge n, Schlüssel k,
untere Schranke u, obere Schranke o */
/* output: Position p */
m = (u+o)/2;
if (F[m] == k) return m;
if ( u == o) return -1;
if (F[m] > k) return BinarySearchRec(F,k,u,m-1);
return BinarySearchRec(F,k,m+1,o);
}
Aufwands Analyse
BearbeitenDas Terminierungs-Theorem besagt, dass der Algorithmus BinarySearch für jede endliche Eingabe F nach endlicher Zeit terminiert. In jedem Rekursionsschritt verkürzt sich die Länge des betrachteten Arrays F um mehr als die Hälfte. Nach endlichen vielen Schritten hat das Array nur noch ein Element und die Suche endet entweder erfolgreich oder erfolglos. Falls das Element vorher gefunden wird terminiert der Algorithmus schon früher.
Das Korrektheits-Theorem besagt, dass falls das Array F ein Element k enthält, gibt BinarySearch(F.k) den Index eines Vorkommens von k zurück. Ansonsten gibt BinarySearch (F,k) den Wert ‐1 zurück. Beweisen kann man das durch die verallgemeinerte Induktion nach der Länge n von F. n=1: Der erste Aufruf von BinarySearchRec ist BinarySearchRec(F,k,0,0) und somit m=0. Ist F[0]=k so wird 0 zurückgegeben, ansonsten ‐1 da 0=0. n>1: Der erste Aufruf von BinarySearchRec ist BinarySearchRec(F,k,0,n‐1) und somit m=(n‐1)/2. Ist F[m]=k, so wird m zurückgegeben. Ansonsten wird rekursiv auf F[0...m‐1] oder F[m+1...n] fortgefahren. Da die Folge sortiert ist, kann k nur in einem der beiden Teile vorhanden sein.
Da die Liste nach jedem Aufruf halbiert wird, haben wir nach dem ersten Teilen der Folge noch n/2 Elemente, nach dem zweiten Schritt n/4 Elemente, nach dem dritten Schritt n/8 Elemente... daher lässt sich allgemein sagen, dass in jedem i-ten Schritt maximal Elemente, das heißt Vergleiche bei der Suche. Im besten Fall hat die Suche nur einen Vergleich, weil der Suchschlüssel genau in der Mitte liegt. Im schlechtesten Fall und im Durchschnitt für eine erfolgreiche und eine erfolglose Suche liegt die Anzahl der Vergleiche bei .
Rekursionsgleichung
BearbeitenFür die erfolglose Suche ergibt sich folgende Rekursionsgleichung.
Das Auflösen von T(n) nach Induktion ergibt eine Laufzeit für eine erfolglose, also Worst-Case, Suche.
Iterativer Algorithmus
Bearbeitenint BinarySearch(int[] F, int k) {
/* input: Folge F der Länge n, Schlüssel k */
/* output: Position p (0 ≤ p ≤ n-1) */
int u = 0;
int o = F.length-1;
int m;
while (u <= o) {
m = (u+o)/2;
if (F[m] == k)
return m;
else
if (k < F[m])
o = m-1;
else
u = m+1;
}
return -1;
}
Der erste Teil des Algorithmus ist die Initialisierung. Die while Schleife, besagt, dass so lange wiederholt werden soll, bis die angegebenen Schranken erreicht sind. Die if Anweisung ist die Abbruchbedingung. Der letzte Teil des Algorithmus (else) passt die obere, bzw. untere Schranke an.
Vergleich der Suchverfahren
Bearbeiten| Verfahren / #Elemente | ||||
|---|---|---|---|---|
| sequenziell (n/2) | ||||
| binär |
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.1.2 zu finden.
Fibonacci Suche
BearbeitenDieses Kapitel behandelt die Fibonacci Suche. Die im vorherigen Kapitel behandelte binäre Suche hat Nachteile. Die binäre Suche ist der am häufigsten verwendete Algorithmus zur Suche in sortierten Arrays. Die Sprünge zu verschiedenen Testpositionen sind allerdings immer recht groß. Dies kann nachteilig sein, wenn das Array nicht vollständig im Speicher vorliegt (oder bei Datenträgertypen wie Kassetten). Außerdem werden neue Positionen durch Division berechnet und je nach Prozessor ist dies eine aufwändigere Operation als Addition und Subtraktion. Daher nehmen wir die Fibonacci Suche als eine weitere Alternative.
Fibonacci Zahlen
BearbeitenZur Erinnerung, die Folge der Fibonacci Zahlen für ist definiert durch
für
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 |
Anstatt wie bei der binären Suche das Array in gleich große Teile zu teilen, wird das Array in Teilen entsprechend der Fibonacci-Zahlen geteilt. Es wird zunächst das Element an Indexposition m betrachtet, wobei m die größte Fibonaccizahl ist, die kleiner als die Arraylänge ist. Nun fährt man rekursiv mit dem entsprechenden Teilarray fort.
Rekursive Fibonacci Suche
Bearbeitenpublic int fibonacciSearch(int[] arr, int elem) {
return fibonacciSearchRec(arr,elem,0,arr.length-1);
}
public int fibonacciSearchRec(int[] arr, int elem, int u, int o) {
int k = 0;
while (fib(k) < o-u) k++;
if (elem == arr[u+fib(--k)])
return u+fib(k);
if (u == o)
return -1;
if (elem < arr[u+fib(k)])
return fibonacciSearchRec(arr, elem, u, u+fib(k)-1);
return fibonacciSearchRec(arr ,elem, u+fib(k)+1, o);
}
Beispiel
Bearbeiten| 9 | 19 | 21 | 34 | 87 | 102 | 158 | 159 | 199 | 205 |
Wo befindet sich die 133?
- fibonacciSearchRec(arr,133,0,9)
- fib(6)=8 < 9-0 (und maximal)
- arr[fib(6)+0] = arr[8] = 199 > 133
- fibonacciSearchRec(arr,133,0,7)
- fib(5)=5 < 7-0 (und maximal)
- arr[fib(5)+0] = arr[5] = 102 < 133
- fibonacciSearchRec(arr,133,6,7)
- fib(0)=0 < 7-6 (und maximal)
- arr[fib(0)+6] = arr[6] = 158 > 133
- fibonacciSearchRec(arr,133,6,6)
- Suche erfolglos
Wo befindet sich die 87?
- fibonacciSearchRec(arr,87,0,9)
- fib(6)=8 < 9-0 (und maximal)
- arr[fib(6)+0] = arr[8] = 199 > 87
- fibonacciSearchRec(arr,87,0,7)
- fib(5)=5 < 7-0 (und maximal)
- arr[fib(5)+0] = arr[5] = 102 > 87
- fibonacciSearchRec(arr,87,0,4)
- fib(4)=3 < 4-0 (und maximal)
- arr[fib(4)+0] = arr[3] = 34 < 87
- fibonacciSearchRec(arr,87,4,4)
- Suche erfolgreich
Aufwands Analyse
BearbeitenDie Fibonacci Suche hat dieselbe Komplexität wie die binäre Suche. Die Anzahl der Vergleiche im besten Fall ist 1 und die Anzahl der Vergleiche im Durchschnitt (erfolgreich/erfolglos) und im schlechtesten Fall ist . Die nötigen Fibonaccizahlen können vorab berechnet und in einem (statischen) Array gespeichert werden. Für Arrays mit weniger als 100.000.000 Elementen werden “nur” die ersten 50 Fibonaccizahlen benötigt. Als Operationen können nur Subtraktion und Addition genutzt werden und die “Sprünge” zwischen Arrayposition ist im Durchschnitt geringer als bei binärer Suche.
Einleitung Suchen in Texten
BearbeitenNun behandeln wir das Suchen in Texten. Das Problem ist das Suchen eines Teilwortes in einem langen anderen Wort. Dies ist eine typische Funktion der Textverarbeitung. Nun ist eine effiziente Lösung gesucht. Das Maß der Effizienz ist hierbei die Anzahl der Vergleiche zwischen den Buchstaben der Worte. Den Vergleich von Zeichenketten nennt man String-Matching und eine nicht übereinstimmende Position nennt man Mismatch.
Vorgegebene Daten
Bearbeiten- Worte als Array:
- text[] zu durchsuchender Text
- pat[] 'Pattern', gesuchtes Wort
- Wortlängen:
- n Länge des zu durchsuchenden Textes
- m Länge des gesuchten Wortes
- Alphabet, leerer String
Abstrakte Algorithmenbeschreibung:
Eingabe: text[], pat[]
Ausgabe: Index i mit text[i...i+m]=pat[1...m+1] oder -1 falls das gesuchte Wort nicht im Text vorkommt.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5 zu finden.
Einleitung Suchen in Texten
BearbeitenNun betrachten wir einen naiven Algorithmus zur Textsuche.
Problem der Worterkennung
BearbeitenDirekte Lösung - brute force
| a | b | a | c | a | a | b | a | c | c | a | b | a | c | a | b | a | a | b | b |
| a (1) | b (2) | a (3) | c (4) | a (5) | b (6) |
a (7) b a c a b
a (8) b (9) a c a b
....
a (22) b (23) a (24) c (25) a (26) b (27)
Pseudocode Brute Force Algorithmus
Bearbeitenfor i=1 to n-m+1 do
- Falls pat = text[i...i+m-1] gib i zurück;
Gib -1 zurück
In Java:
int bruteforce_search(char[] text, char[] pat){
int i,j;
for(i = 0; i < text.length - pat.length+1; i++){
for(j = 0; j < pat.length && pat[j] == text[i+j]; j++)
;
if(j == pat.length)
return i;
}
return -1;
}
Analyse
BearbeitenDas Terminierungstheorem besagt, dass der Algorithmus bruteforce_search bei endlicher Eingabe nach endlich vielen Schritten terminiert.
Das Theorem der Korrektheit besagt, wenn text die Zeichenkette pat enthält, so gibt bruteforce_search(text,pat) den Startindex des ersten Vorkommens von pat zurück, ansonsten -1.
Das Theorem der Laufzeit besagt, dass der Algorithmus bruteforce_search einen Worst-Case Laufzeit von hat. Beweisen lässt sich das durch eine einfache Schleifenanalyse. Die äußere for-Schleife wird maximal (n-m)-mal durchlaufen, die innere for-Schleife wird jedes mal maximal m-mal durchlaufen:
Dafür hat bruteforce_search nun einen Platzbedarf von . Kann man durch zusätzlichen Platzbedarf die Laufzeit verbessern?
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5 zu finden.
Einleitung Algorithmus von Knuth-Morris-Pratt
BearbeitenAuf dieser Seite behandeln wir den Algorithmus von Knuth-Morris-Pratt. Die Idee ist, dass bereits gelesene Informationen bei einem Mismatch genutzt werden. Kommt es an Stelle j von pat zum Mismatch, so gilt:
pat[1...j-1]=text[i...i+j-2]
| a | b | a | c | a | a | b | a | c | c | a | b | a | c | a | b | a | a | b | b |
| a (1) | b (2) | a (3) | c (4) | a (5) | b (6) |
Das a an Stelle 5 ist das Suffix von pat[1..5]. Nun gilt: schiebe Muster um 4, überprüfe weiter ab Position 6 im Text, ab Position 2 im Muster
a b (7) a c a b
Das erste a ist nun das Präfix
a (8) b (9) a (10) c (11) a (12) b
a (13) b a c a b
a (14) b (15) a (16) c (17) a (18) b (19)
Realisierung mit Fehlerfunktion
BearbeitenBestimme für jedes j der Länge f[j] des längsten Präfixes von pat der Suffix von pat[1..j] ist. Gibt es einen Fehler an Stelle j, dann verschiebe die Suchposition im Muster auf j:=f[j-1]+1=border[j].
| Position j im Pattern | 1 | 2 | 3 | 4 | 5 | 6 |
| Pattern pat[j] | a | b | a | c | a | b |
| Längster Präfix f[j] | 0 | 0 | 1 | 0 | 1 | 2 |
| Verschiebeposition | 0 | 1 | 1 | 2 | 1 | 2 |
border im Detail
BearbeitenPreprocessing bedeutet, dass für jedes das größte k so bestimmt wird, dass pat [1...k-1] ein echter Suffix von pat[1...j-1] ist. Genauer berechnet und als border bezeichnet wird:
Bei einem Mismatch an Position j verschiebe die Position im Text auf i:=i+ border[j] )oder 1 falls nicht definiert, z.B. erste Position) und die Position im Suchmuster auf j:=border[j]
Die border-Tabelle
BearbeitenBeispiel: Drei Zeilen j, pat[j] und border [j]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | j |
| a | b | a | a | b | a | b | a | a | b | a | a | b | pat[j] |
| 0 | 1 | 1 | 2 | 2 | 3 | 4 | 3 | 4 | 5 | 6 | 7 | 5 | border[j] |
Dieses Beispiel ist ein so genannter Fibonacci String.
Algorithmus von border
Bearbeiten
Eingabe: char-Array pattern[]
Ausgabe: int-Array border[]
int[] border = new int[pattern.length];
for(int k = 0; k < border.length; k++){
border[k] = 0;
}
int i = 1, j = 0;
while(i < border.length){
while(i+j < border.length-1 &&
pattern[j] == pattern[i+j]){
border[i+j+1] = max(border[i+j+1],j+1);
j++;
}
i++;
}
sborder als Verbesserung von border
BearbeitenProblem:
| pat: | a | b | a | a | b | a | - | - | ||||||
| text: | - | - | - | - | - | - | a | b | a | a | b | c | - | - |
Hier gibt es ein mismatch an der Stelle j=g, border[6]=3. Daher muss um 3 verschoben werden.
| pat: | a | b | a | a | b | a | - | - | |||||||||
| text: | - | - | - | - | - | - | a | b | a | a | b | c | - | - |
Nun haben wir als Result sofort wieder ein Mismatch. Wir wissen bereits, dass an der Mismatch Stelle kein a stehen darf.
Verbesserung:
Falls kein deratiges k existiert, dann 0.
Beispeil vier Zeilen mit j, pat[j], border[j] und sborder[j]:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | j |
| a | b | a | a | b | a | b | a | a | b | a | a | b | pat[j] |
| 0 | 1 | 1 | 2 | 2 | 3 | 4 | 3 | 4 | 5 | 6 | 7 | 5 | border[j] |
| 0 | 1 | 0 | 2 | 1 | 0 | 4 | 0 | 2 | 1 | 0 | 7 | 1 | sborder[j] |
Algorithmus
Bearbeiten
Eingabe: char-Array text[], char-Array pattern[]
Ausgabe: true/false
int[] sborder = new int[pattern.length];
for(int k = 0; k < sborder.length; k++){
sborder[k] = 0;
}
int i = 1, j = 0;
while(i < sborder.length){
while(i+j < sborder.length-1 &&
pattern[j] == pattern[i+j]){
if(pattern [j+1] == pattern[i+j+1])
sborder[i+j+1] = max(sborder[i+j+1],j+1);
j++;
}
i++;
}
i = 0;
j = 0;
while(i < text.length() - pattern.length() + 1){
while(j < pattern.length() && text[i+j] == pattern[j]){
j++;
}
if(j == pattern.length()) return true;
i = i + max(border[j], 1);
j = border[j];
}
Analyse
BearbeitenDas Theorem der Terminierung besagt, dass der Algorithmus von Knuth-Morris-Pratt für endliche text[] und pat[] eine endliche Laufzeit hat.
Das Theorem der Korrektheit besagt, wenn text die Zeichenkette pat enthält, so gibt der Algorithmus von Knu5‐Morris‐Pra5 TRUE zurück, ansonsten FALSE.
Das Theorem der Laufzeit besagt, dass der Algorithmus von Knutt-Morris-Pratt eine Worst-Case Laufzeit von hat. Beweisen kann man das durch eine einfache Schleifenanalyse: für die Berechnung von sborder und </math> \Theta (n) </math> für die Hauptschleife. Der zusätzliche Platzbedarf des Algorithmus von Knutt-Morris-Pratt ist .
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5 zu finden.
Sortieren
BearbeitenDieses Kapitel gibt eine grundlegende Einführung in das Thema Sortieren. Sortieren ist ein grundlegendes Problem in der Informatik. Es beinhaltet das Ordnen von Dateien mit Datensätzen, die Schlüssel enthalten und das Umordnen der Datensätze, so, dass eine klar definierte Ordnung der Schlüssel (numerisch/alphabetisch) besteht. Eine Vereinfachung ist die Betrachtung der Schlüssel, z.B. ein Feld von int-Werten.
Ordnung
Bearbeiten- Partielle Ordnung
- Sei M eine Menge und binäre Relation.
- Es gilt:
- Reflexivität
- Transitivität
- Antisymmetrie
- Es gilt:
- Strikter Anteil einer Ordnungsrelation
- Totale Ordnung
- Partielle Ordnung
- Trichotomie ("Dreiteilung")
Grundbegriffe
BearbeitenDas Verfahren ist intern, wenn auf Hauptspeicherstruktur, wie Felder und Listen sortiert wird. Hingegen ist es extern, wenn die Datensätze auf externen Medien, wie Festplatten und weitere sortiert werden. Die Annahmen sind eine totale Ordnung, aufsteigend vs. absteigend und der Platzbedarf.
Problembeschreibung
BearbeitenAls Eingabe haben wir eine Folge von Zahlen . Als Ausgabe haben wir die Permutation der Zahlen mit der Eigenschaft . Die Sortierung erfolgt nach einem Schlüssel, z.B. Zahlen. In Programmen ist es übertragbar auf beliebige Datenstrukturen mit Schlüssel.
Stabilität
BearbeitenEin Sortierverfahren heißt stabil, wenn es die relative Reihenfolge gleicher Schlüssel in der Datei beibehält. Beispiel: alphabetisch geordnete Liste von Personen soll nach Alter sortiert werden. Personen mit gleichem Alter sollen weiterhin alphabetisch geordnet bleiben:
Name Alter Name Alter Aristoteles 24 Aristoteles 24 Platon 28 SORTIEREN → Platon 28 Sokrates 30 Theophrastos 28 Theophrastos 28 Sokrates 30
Sortieralgorithmen
BearbeitenJava Stub
Bearbeitenpublic class InsertionSort extends Sort {
/*
* Sortiert die Sequenz a nach dem Verfahren
* „Sortieren durch Einfügen“
*/
@Override
public void execute(int[] a) {
// Elemente: a[0], … , a[n-1]
int n=a.length;
int x;
int j;
// HIER KOMMT DER SORTIERALGORITHMUS
// assert: a[0] <= … <= a[n-1]
}
}
Vergleichsbasiertes Sortieren
BearbeitenDas vergleichbasierte Sortieren ist ein wichtiger Spezialfall des Sortierproblems. Zur Sortierung können nur direkte Vergleiche zweier Werte benutzt werden. Der Wertebereich der Schlüssel kann beliebig sein. Als Eingabe haben wir ein Array ganzer Zahlen und als Ausgabe ein sortiertes Array mit den selben Zahlen mit erhaltenen Mehrfachvorkommen. Einige Sortierverfahren sind effizienter, wenn Listen anstatt Arrays benutzt werden.
Sortierinterface in Java
Bearbeitenpublic interface Sort {
/**
* sorts the given array.
* @param toSort - array to sort.
*/
public void execute(int[] toSort);
}
Ausblick
BearbeitenAuf den folgenden Seiten werden die Sortieralgorithmen Insertion Sort, Selection Sort, Merge Sort und Quick Sort behandelt.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2 zu finden.
InsertionSort
BearbeitenDieses Kapitel behandelt die Sortiermethode InsertionSort oder auch Sortieren durch Einfügen genannt. Die Idee des Algorithmus ist, die typische menschliche Vorgehensweise, etwa beim Sortieren eines Stapels von Karten umzusetzen. Das heißt es wird mit der ersten Karte ein neuer Stapel gestartet. Anschließend nimmt man jeweils die nächste Karte des Originalstapels und fügt diese an der richtigen Stelle im neuen Stapel ein.
Beispiel
BearbeitenJava Code
Bearbeitenvoid InsertionSort(int[] F) {
int m,j;
for (int i = 1; i < F.length; i++){
j = i;
m = F[i];
while (j > 0 && F[j-1] > m) {
/*verschiebe F[j-1] nach rechts */
F[j] = F[j-1];
j--;
}
F[j] = m;
}
}
Das Array hat F.length viele Elemente von Position 0 bis F.Length-1. Wenn F[j-1] größer m ist, dann wird F[j-1] nach rechts verschoben. Am Ende des Algorithmus wird F[i] an Position F[j] gesetzt.
Analyse
BearbeitenTheorem der Terminierung
BearbeitenDas Theorem der Terminierung besagt, dass der Algorithmus InsertionSort für jede Eingabe int[] F nach endlicher Zeit terminiert.
Beweis
BearbeitenDie Laufvariable i in der äußeren for‐Schleife wird in jedem Durchgang um eins erhöht und wird damit irgendwann die Abbruchbedingung (eine Konstante)erreichen. Die Laufvariable j der inneren while‐Schleife wird in jedem Durchgang um eins verringert und somit die Schleifenbedingung j>0 irgendwann nicht mehr erfüllen.
Theorem der Korrektheit
BearbeitenDas Theorem der Korrektheit besagt, dass der Algorithmus InsertionSort das Problem des vergleichsbasierten Sortierens löst. Beweisen
Beweis
BearbeitenWir zeigen, dass die folgende Aussage eine Invariante der äußeren for‐Schleife ist (d.h. sie ist am Ende eines jeden Schleifendurchgangs gültig): Das Teilarray F[0..i] ist sortiert Damit gilt auch, dass nach Abbruch der for‐Schleife das Array F[0..n]=F (mit n=F.length‐1) sortiert ist. Zu zeigen ist nun, dass am Ende jeden Durchgangs der äußeren for Schleife F[0...i] sortiert ist. Dies wird durch Induktion nach i gezeigt. Für i=1 gilt im ersten Durchgang wird das erste Element F[0] mit dem zweiten Element F[1] verglichen und ggfs. getauscht um Sortierung zu erreichen (while‐Bedingung). Für gilt angenommen F[0...i] ist am Anfang der äußeren for‐Schleife im Durchgang i+1 sortiert. In der while‐Schleife werden Elemente solange einen Platz weiter nach hinten verschoben, bis ein Index k erreicht wird, sodass alle Elemente mit Index 0..k‐1 kleiner/gleich dem ursprünglichen Element an Index i+1 sind (Induktionsbedingung) und alle Elemente mit Index k+1...i+1 größer sind (while‐Bedingung). Das ursprüngliche Element an Index i+1 wird dann an Position k geschrieben. Damit gilt, dass F[0...i+1] sortiert ist.
Theorem der Laufzeit
BearbeitenDas Theorem der Laufzeit besagt, dass die Anzahl der Vergleichsoperationen von Insertion Sort im besten Fall ist und im durchschnittlichen und schlechtesten .
Beweis
BearbeitenFür die Aufwandsanalyse sind die Anzahl der Vertauschungen und der Vergleiche relevant. Allerdings dominieren die Vergleiche die Vertauschungen, das heißt es werden wesentlich mehr Vergleiche als Vertauschungen benötigt. Wir müssen in jedem Fall alle Elemente i:=1 bis n-1 durchgehen, d.h. immer Faktor n-1 für die Anzahl der Vergleiche. Dann müssen wir zur korrekten Einfügeposition zurückgehen
Im besten Fall ist die Liste schon sortiert. Die Einfügeposition ist gleich nach einem Schritt an Position i-1, d.h. die Anzahl der Vergleiche ist gleich der Anzahl der Schleifendurchläufe = n-1. Bei jedem Rückweg zur Einfügeposition nimmt man den Faktor 1. Somit beträgt die Gesamtzahl der Vergleiche: . Für große Listen lässt sich abschätzen. Damit haben wir einen linearen Aufwand.
Im mittleren Fall ist die Liste unsortiert. Die Einfügeposition befindet sich wahrscheinlich auf der Hälfte des Rückwegs. Bei jedem der n-1 Rückwege, muss ein (i-1)/2 Vergleich addiert werden. Die Gesamtzahl der Vergleiche beträgt dann:
Daraus ergibt sich ein quadratischer Aufwand, wenn konstante Faktoren nicht berücksichtigt werden.
Im schlechtesten Fall ist die Liste absteigend sortiert. Die Einfügeposition befindet sich am Ende des Rückgabewertes bei Position 1. Bei jedem der n-1 Rückwege müssen i-1 Elemente verglichen werden (d.h. alle vorherigen Elemente F[1...i-1]). Analog zu vorhergehenden Überlegungen, gibt es hier aber die doppelte Rückweglänge. Daraus ergibt sich die Gesamtanzahl der Vergleiche:
Daraus ergibt sich ein quadratischer Aufwand, wenn konstante Faktoren nicht berücksichtigt werden.
Optimierung
BearbeitenIn der vorgestellten Version des Algorithmus wird die Einfügeposition eines Elements durch (umgekehrte) sequenzielle Suche gefunden. Verwendet man hier binäre Suche (das Teilarray vor dem aktuellen Element ist sortiert!) kann die Anzahl der Vergleichsoperationen gesenkt werden zu O(n log n) (genauere Analyse zeigt, dass die Zahl noch kleiner ist)
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.2 zu finden.
SelectionSort
BearbeitenDieses Kapitel behandelt die Suchmethode SelectionSort. Die Idee dieses Suchalgorithmus ist, den jeweils größten Wert im Array zu suchen und diesen an die letzte Stelle zu tauschen. Anschließend fährt man mit der um 1 kleineren Liste fort.
Beispiel
BearbeitenJava Code
Bearbeitenvoid SelectionSort(int[] F) {
int meinSackJuckt = F.length -1;
while (meinSackJuckt >= 0) {
/*bestimme größtes Element links v. Marker*/
int max = 0; /* Indexposition*/
for (int i = 1; i <= meinSackJuckt; i++){
if (F[i] > F[max])
max = i;
swap(F, meinSackJuckt, max);
meinSackJuckt--; /*verkleinere Array */
}
void swap(int[] F, int idx1, int idx2) {
int tmp = F[idx1];
F[idx1] = F[idx2];
F[idx2] = tmp;
}
In Java benutzt man die Hilfsmethode swap, welche zwei Elemente im Array vertauscht.
Analyse
BearbeitenTheorem der Terminierung
BearbeitenDas Theorem der Terminierung besagt, dass der Algorithmus SelectionSort für jede Eingabe int[]F nach endlicher Zeit terminiert.
Beweis
BearbeitenDie Variable marker wird zu Anfang des Algorithmus auf einen positiven endlichen Wert gesetzt und in jedem Durchgang der äußeren while‐Schleife um 1 verkleinert. Abbruch der while Schleife erfolgt, wenn marker kleiner 0 ist, also wird die while‐Schleife endlich oft durchlaufen. Die innere for‐Schleife hat in jedem Durchgang marker‐viele (also endlich viele) Durchläufe.
Theorem der Laufzeit
BearbeitenDas Theorem der Laufzeit besagt, dass der Algorithmus SelectionSort eine Laufzeit von hat im besten, mittleren und schlechtesten Fall.
Beweis
BearbeitenDie äußere while‐Schleife wird genau n‐mal (n=F.length) durchlaufen. Dort werden somit n Vertauschungen vorgenommen (=jeweils konstanter Aufwand). Die innere for‐Schleife hat im i‐ten Durchlauf der while‐Schleife n‐i Durchläufe mit jeweils einem Vergleich, deswegen insgesamt
Die Anzahl der Vergleiche ist im besten, mittleren und schlechteste Fall identisch, da immer das komplette Array durchlaufen wird.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.3 zu finden.
BubbleSort
BearbeitenDieses Kapitel behandelt die Suchmethode BubbleSort. Es handelt sich hierbei um ein sehr bekanntes, aber nicht besonders effizientes Sortierverfahren. Es ist eine einfach zu implementierende zugrunde liegende Vorstellung. Bei einer vertikalen Anordnung von Elementen in Form von Luftblasen (bubbles) werden wie in einer Flüssigkeit von alleine sortiert, da die größeren Blasen die kleiner „überholen“. Das Grundprinzip ist somit die Folge immer wieder zu durchlaufen und dabei benachbarte Elemente, die nicht die gewünschte Sortierreihenfolge haben, zu vertauschen. Das bedeutet Elemente die größer sind als ihre Nachfolger, überholen diese.
Beispiel
BearbeitenJava Code
Bearbeitenvoid BubbleSort(int[] F) {
for (int n= F.length; n >1; n=n-1) {
for (int i =0; i < F.length-1; i++) {
if (F[i] > F[i+1]){
swap(F, i, i+1);
}
}
}
}
Hierbei handelt es sich um die einfachste Form, doch der Algorithmus kann auch optimiert werden. Wir haben beobachtet, dass die größte Zahl in jedem Durchlauf automatisch an das Ende der Liste rutscht. Daraus folgt in jedem Durchlauf j reicht die Untersuchung bis Position n-j, das heißt im j.ten Durchlauf sind die Elemente zwischen den Positionen n-j und n-1 sortiert. Wenn keine Vertauschung mehr stattfindet, soll das Programm abbrechen.
void BubbleSort(int[] F) {
boolean swapped;
int n = F.length;
do {
swapped = false;
for (int i =0; i < n-1; i++) {
if (F[i] > F[i+1]){
swap(F, i, i+1);
swapped = true;
}
}
n--;
}while (swapped);
}
Aufwand
BearbeitenIm besten Fall beträgt der Aufwand n. Im mittleren Fall ohne Optimierung und mit Optimierung . Im schlechtesten Fall ohne Optimierung beträgt der Aufwand und mit Optimierung .
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.4 zu finden.
MergeSort
BearbeitenIn diesem Kapitel wird der Sortieralgorithmus MergeSort behandelt.
Rückblick
BearbeitenDie bisherige Verfahren erforderten einen direkten Zugriff auf einzelne Elemente (z.B. in einem Array). Sie sind besonders geeignet für internes Sortieren. Allerdings gibt es Probleme, wenn Daten sortiert werden sollen, die nicht in den den Hauptspeicher passen. Daher brauchen wir andere Verfahren, die nicht zwingend Elemente intern verwalten. Das Prinzip dieser Algorithmen ist das Sortieren in mehreren Phasen oder Schritten.
Idee
BearbeitenMergeSort ist ein Divide-and-Conquer Algorithmus zum vergleichsbasierten Sortieren. Zuerst wird die zu sortierende Folge in zwei Teile geteilt. Anschließend werden beide Teile voneinander getrennt sortiert. Zuletzt werden beide Teilergebnisse in der richtigen Reihenfolge zusammen gemischt.
Beispiel
BearbeitenAlgorithmus
Bearbeitenvoid mergeSort(int[] F) {
int[] tmpF = new int[F.length];
mergeSort(F, tmpF, 0, F.length -1);
}
void mergeSort(int[] F, int[] tmpF, int left,int right)
{
if (left < right) {
int m = (left + right)/2;
mergeSort(F, tmpF, left, m);
mergeSort(F, tmpF, m+1, right);
merge(F, tmpF, left, m+1, right);
}
}
void merge(int[] F, int[] tmpF, int startLeft, int startRight, int endRight) {
int endLeft = startRight-1;
int tmpPos = startLeft;
int numElements = endRight – startLeft +1;
while (startLeft <= endLeft && startRight <= endRight)
if (F[startLeft] < F[startRight])
tmpF[tmpPos++] = F[startLeft++];
else
tmpF[tmpPos++] = F[startRight++];
while (startLeft <= endLeft)
tmpF[tmpPos++] = F[startLeft++];
while (startRight <= endRight)
tmpF[tmpPos++] = F[startRight++];
for (int i = 0; i < numElements; i++, endRight--)
F[endRight] = tmpF[endRight];
}
Das Abbruchkriterium für den rekursiven Aufruf ist eine einelementige Liste.Der Misch-Vorgang erfordert in der Regel doppelten Speicherplatz, da eine neue Folge aus den beiden Sortierten generiert werden muss. Eine Alternative ist das Mischen in einem Feld (in-place), das erfordert aber aufwendiges Verschieben.
Analyse
BearbeitenTheorem der Terminierung
BearbeitenDas Theorem der Terminierung besagt, dass der Algorithmus MergeSort für jeden Eingabe int[]F nach endlicher Zeit terminiert.
Beweis
BearbeitenZeige zunächst, dass jeder Aufruf mergeSort(int[] F, int[] tmpF, int left,int right) terminiert:
- Falls lef < right nicht gilt, terminiert der Aufruf sofort
- Andernfalls rufen wir mergeSort rekursiv auf, wobei entweder lef einen echt größeren oder right einen echt kleineren Wert erhält. In jedem Fall wird nach einem gewissen rekursiven
Abstieg irgendwann lef<right nicht mehr gelten.
Theorem der Korrektheit
BearbeitenDas Theorem der Korrektheit besagt, dass der Algorithmus MergeSort das Problem des vergleichsbasierten Sortierens löst.
Beweis
BearbeitenDurch Induktion nach n = F.length. Annahme n=2 für eine ganze Zahl k.
- n=1: Für n=1 ist der erste Aufruf der mergeSort Hilfsmethode mergeSort(F, tmpF, 0, 0)
und somit gilt nicht lef < right. Die Methode terminiert ohne Änderung an F. Dies ist korrekt, da jedes einelementige Array sortiert ist.
- n/2 → n: Sei F[0...n‐1] ein beliebiges Array. Der erste Aufruf mergeSort(F, tmpF, 0, n-1) erfüllt lef<right und es werden folgende Rekursive Aufrufe getätigt: mergeSort(F, tmpF, 0, n/2-1) mergeSort(F, tmpF, n/2, n-1) Beide Aufrufe erhalten ein Array der Länge n/2. Nach Induktionsannahme gilt, dass anschliessend sowohl F[0...n/2‐1] als auch F[n/2...n‐1] separat sortiert sind. Noch zu zeigen ist, dass merge korrekt zwei sortierte Arrays in ein sortiertes Array mischt.
Theorem der Laufzeit
BearbeitenDas Theorem der Laufzeit besagt, dass der Algorithmus MergeSort eine Laufzeit von hat. Diese Laufzeit ist die selbe für den besten, mittleren und schlechtesten Fall.
Beweis
Bearbeiten
Nun wenden wir das Master Theorem an.
Im 2. Fall, wenn
Hier ist a=2 und b=2 und es folgt
Es ist zudem f(n)=n und es gilt für k=0:
Es folgt
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.5 zu finden.
Zwischenbemerkungen
BearbeitenAn dieser Stelle gibt es einige Zwischenbemerkungen zu den vorgestellten Sortieralgorithmen.
Einordnung der elementaren Sortierverfahren
Bearbeiten| Implementierung Array | Implementierung Liste | |
| greedy | selection sort, bubble sort | insertion sort |
| divide-and-conquer | quicksort | merge sort |
Eigenschaften
BearbeitenDivide and conquer bedeutet teile und herrsche. Dabei wird das eigentliche Problem so lange in kleiner und einfachere Teilprobleme zerlegt, bis man diese lösen kann. Oft können Teilprobleme parallel gelöst werden. Des Weiteren sind Teilprobleme „eigenständige“ Probleme. Anschließend werden die Teillösungen zu einer Gesamtlösung zusammengeführt.
Greedy bedeutet gierig. Hierbei wird schrittweise ein Folgezustand ausgewählt, der aktuell den größten Gewinn und das beste Ergebnis verspricht. Die Auswahl des Folgezustands erfolgt anhand von Bewertungsfunktionen und Gewichtsfunktionen. Ein Problem dabei ist, dass oft nur ein lokales Maximum gewählt wird. Mehr dazu im Thema Entwurfsmuster.
Generische Implementierung
BearbeitenAlgorithmen werden „parametrisiert“ durch Vergleichsoperator. Im Paket java.lang gibt es dafür ein Interface Comparable. Der Aufruf der Vergleichsmethode a.compareTo(b) liefert ein Zahl <0, =0, >0 für a<b, a=b und a größer b. Das Muster für Objekte vom Referenztyp Comparable lautet:
public class MyObject implements Comparable {
MyType data;
public int compareTo (MyObject obj) {
if („this.data < obj.data“) return -1;
if („this.data = obj.data“) return 0;
if („this.data > obj.data“) return 1;
}
}
Das Muster für Aufrufe in Klassenmethoden bei Suchverfahren lautet:
public static int binarySearch( Comparable[] f,
Comparable a, int l, int r) {
int p = (l+r)/2;
int c = f[p].compareTo(a);
... }
Listenimplementierung generisch
Bearbeiten
public class MyObject implements Comparable {. . .}
public class Node {
MyObject data;
Node next;
}
public class OrderedList {
private Node head;
public OrderedList sort ( ) {. . .}
Interne Hilfsmethoden
Bearbeiten- int findMin(){...}
- F.findMin() bestimmt den Index des minimalen Elements von OrderedList F
- void insertLast(int a)
- F.insertLast(a) fügt Element mit Index (Key) a an das Ende von F an
- void deleteElem(int a)
- F.deleteElem(a) löscht Element mit Index a aus der Liste F
- Aufwand: jeweils = O(n), wenn n = Anzahl der Objekte in Liste
MergeSort generisch
Bearbeiten
public class OrderedList {
OrderedNode head;
int length;
// ...
/** * Sorts this list in non-descending order */
public void mergeSort() {
OrderedList aList, bList; // the divided lists
OrderedNode aChain; // start of first node chain
OrderedNode bChain; // start of second node chain
OrderedNode tmp; // working node for split
// trivial cases
if ( (head==null) || (head.next == null) )
return;
// divide: split the list in two parts
aChain = head;
tmp = head; // init working node for split
// advance half of the list
for (int i=0; i < (length-1) / 2; i++)
tmp=tmp.next;
// cut chain into aChain and bChain
bChain=tmp.next;
tmp.next=null;
// encapsulate the two node chains in two lists
aList = new OrderedList();
aList.head=aChain;
aList.length=length/2;
bList = new OrderedList();
bList.head=bChain;
bList.length=length - aList.length;
// conquer: recursion
aList.mergeSort(); bList.mergeSort();
// join: merge
merge(aList, bList);
}
}
Aus Gründen der Übersichtlichkeit erzeugt dieses Programm im Divide-Schritt jeweils gekapselte Zwischenlisten vom Typ OrderedList. In der Praxis würde man hierauf verzichten und rein auf Knoten-Ketten arbeiten, da insgesamt O(n) Objekte vom Typ OrderedList erzeugt und wieder vernichtet werden(maximal O(log n) davon sind gleichzeitig aktiv).
QuickSort
BearbeitenIn diesem Kapitel wird der Sortieralgorithmus QuickSort behandelt.
Idee
BearbeitenEs gibt eine rekursive Aufteilung (wie bei MergeSort), aber hier werden Mischvorgänge vermieden (speicherintensiv!). Die Teillisten werden in zwei Hälften geteilt bezüglich eines Pivot-Elements, wobei in einer Liste alle Elemente größer als das PivotElement sind und in der anderen Liste alle kleiner. Das Pivot Element ist ein beliebiges Element der Liste/Folge, z.B. das linke, mittlere oder rechte Element.
Beispiel
BearbeitenVertauschen von Elementen
BearbeitenFür gegebenes Pivot-Element p wird die Folge von links durchsuchen, bis das Element gefunden wurde, das größer oder gleich p ist. Und gleichzeitig wird die Folge von rechts durchsuchen, bis das Element gefunden ist, das kleiner p ist. Dabei werden die Elemente ggf. getauscht.
Sortierprinzip
BearbeitenSortieren einer Folge F[u...o] nach dem „divide-and-conquer“Prinzip. Divide heißt die Folge F[u...o] wird in zwei Teilfolgen F[u...p-1] und F[p+1...o] geteilt. Die zwei Teilfolgen haben folgende Eigenschaften:
- F[i] ≤ F[p] für alle i = u,...,p-1
- F[i] > F[p] für alle i = p+1, …, o
Conquer bedeutet, dass die Teilfolgen sortiert werden. Mit combine werden die Teilfolgen zu F[u...o] verbunden. Vergleiche sind an dieser Stelle nicht erforderlich, da die Teilfolgen bereits sortiert sind.
Pivot Element
BearbeitenIm Prinzip muss man nicht das letzte Element als Pivot‐Element wählen. Je nach Verteilung der Daten, kann es sinnvoll sein ein anderes Element zu wählen. Wenn beispielsweise die Liste schon fast sortiert ist, sollte man immer das mittlere Element wählen Eine optimale Rekursion erhält man, wenn man immer den Median als Pivot-Element wählt (dieser ist aber nicht direkt bestimmbar, dafür müsste man die Liste erst sortiert haben. Hat man ein Pivot-Element ausgewählt, tauscht man dies einfach mit dem letzten Element und benutzt den Algorithmus wie zuvor.
Algorithmus
Bearbeitenvoid quickSort(int[] F, int u, int o) {
if (u < o) {
int p = (u+o)/2;
int pn = zerlege(F,u,o,p);
quickSort(F,u,pn-1);
quickSort(F,pn+1,o);
}
int zerlege(int[] F, int u, int o, int p) {
int pivot = F[p];
int i = u;
int j = o;
while (i < j) {
while (F[i] < pivot)
i++;
while (F[j] > pivot)
j--;
if (i < j) {
swap(F,i , j );
}
}
return i;
}
int zerlege(int[] F, int u, int o, int p) {
int pivot = F[p];
//Tausche Pivot-Element mit dem letzten Element
//kann entfallen, wenn immer p=o gewählt wird
swap(F,p, o);
int pn = u;
//bringe kleinere Elemente nach vorne und größere nach hinten
for (int j = u; j < o; j++) {
if (F[j] <= pivot){
swap(F,pn, j );
pn++;
}
}
//bringe das Pivot-Element an die richtige Position und gebe diese zurück
swap(F,pn, o);
return pn;
}
void swap(int[] f, int x, int y){ //Hilfsmethode zum Vertaucshen
int tmp = f[x];
f[x] = f[y];
f[y] = tmp;
}
}
P gibt an ,an welcher Position das Pivot Element ist. Bei diesem Beispiel ist es in der Mitte. Es kann aber auch an Stelle o oder u sein.
Beispiel 1
BearbeitenZerlege (F,0,6,3) mit 3=(0+6)/2
| 8 | 2 | 1 | 5 | 9 | 7 | 3 |
...
| 3 | 2 | 1 | 5 | 9 | 7 | 3 |
Beispiel 2
BearbeitenSei f[8]=5 das Pivot-Element
| 8 | 9 | 2 | 6 | 7 | 3 | 4 | 1 | 5 |
Suche von links aus das Element, welches kleiner als das Pivot-Element ist
| 8 | 9 | 2 | 6 | 7 | 3 | 4 | 1 | 5 |
Vertausche mit dem ersten größeren Element
| 2 | 9 | 8 | 6 | 7 | 3 | 4 | 1 | 5 |
Suche das nächste kleinere Element als die 5
| 2 | 9 | 8 | 6 | 7 | 3 | 4 | 1 | 5 |
Vertausche dieses mit dem zweiten größeren Element
| 2 | 3 | 8 | 6 | 7 | 9 | 4 | 1 | 5 |
Suche wieder das nächste kleinere Element
| 2 | 3 | 8 | 6 | 7 | 9 | 4 | 1 | 5 |
und vertausche dies mit dem dritt größeren Element
| 2 | 3 | 4 | 6 | 7 | 9 | 8 | 1 | 5 |
| 2 | 3 | 4 | 6 | 7 | 9 | 8 | 1 | 5 |
| 2 | 3 | 4 | 1 | 7 | 9 | 8 | 6 | 5 |
nun ist man rechts angekommen und hier wird nun das Pivot-Element getauscht
| 2 | 3 | 4 | 1 | 5 | 9 | 8 | 6 | 7 |
Von nun an steht das Pivot-Element an seiner finalen Position. Alle Elemente links vom Pivot-Element sind kleiner und alle auf der rechten Seite sind größer. Das bedeutet, dass nun ein rekursiver Abstieg für die Folgen
| 2 | 3 | 4 | 1 |
und
| 9 | 8 | 6 | 7 |
beginnen würde. Wenn das letzte Element wieder als Pivot-Element gewählt werden würde, dann hat die erste erste Folge nun das Pivot-Element 1 und in der zweiten Folge währe es das Element 7.
Alternative: Zerlegung mit while-schleifen
BearbeitenMan wählt zuerst ein Pivotelement, beispielsweise das mittlere Element. Nun beginnt man von unten an und vergleicht die Einträge mit dem Pivot. Danach beginnt man von oben und vergleicht die Elemente mit dem Pivot. Wenn ein Element kleiner bzw. größer ist als das Pivot Element, dann wird dieses Element getauscht.
Analyse
BearbeitenTheorem der Terminierung
BearbeitenDas Theorem der Terminierung besagt, dass der Algorithmus quickSort für jede Eingabe int[]F nach endlicher Zeit terminiert.
Beweis
BearbeitenIn jedem rekursiven Aufruf von quickSort ist die Eingabelänge um mindestens 1 kleiner als vorher und die Rekursionsanfang ist erreicht wenn die Länge gleich 1 ist. In der Methode split gibt es nur eine for‐Schleife, dessen Zähler j in jedem Durchgang inkrementiert wird. Da u<o wird die for‐Schleife also nur endlich oft durchlaufen.
Theorem der Korrektheit
BearbeitenDas Theorem der Korrektheit besagt, dass der Algorithmus quickSort das Problem des vergleichsbasierten Sortierend löst.
Beweis
BearbeitenDie Korrektheit der Methode swap ist zunächst offensichtlich. Zeige nun, dass nach Aufruf pn=split(f,u,o,p) für u<o und gilt:
- f[p] wurde zu f[pn] verschoben
Dies ist klar (vorletzte Zeile der Methode split)
- f[i] ≤ f[pn] für i=u,...,pn‐1
pn wird zu anfangs mit u initialisiert und immer dann inkrementiert, wenn die Position f[pn] durch ein Element, das kleiner/gleich dem Pivot‐Element ist, belegt wird.
- f[i] > f[pn] für i=pn+1,...,o
Folgt aus der Beobachtung, dass in 2.) immer „genau dann“gilt. Beachte zudem, dass Element immer getauscht werden, also die Elemente im Array stets dieselben bleiben.
Die Korrektheit der Methode quickSort folgt nach Induktion nach der Länge von f (n=f.length):
- n=1: Der Algorithmus terminiert sofort und ein einelementiges Array ist stets sortiert
- n→n+1: Nach Korrektheit von split steht das Pivot‐Element an der richtigen Stelle und links und rechts stehen jeweils nur kleinere/größere Element. Die beiden rekursiven Aufrufe von quickSort erhalten jeweils ein Array, das echt kleiner als n+1 ist (mindestens das Pivot‐Element ist nicht mehr Teil des übergebenen Arrays). Nach Induktionsannahme folgt die Korrektheit von quickSort.
Theorem der Laufzeit
BearbeitenDas Theorem der Laufzeit besagt, dass wenn als Pivot Element stets der Median des aktuell betrachteten Arrays gewählt wird, so hat der Algorithmus quickSort eine Laufzeit von .
Beweis
BearbeitenEs gilt zunächst, dass split . Ausschlaggebend ist hier die for-Schleife, die genau n-mal durchlaufen wird. Gilt nach dem Aufruf von split stets pn=(u+o)/2 (dies ist gleichbedeutend damit, dass das Pivot‐Element stets der Median ist), so erhalten wir folgende Rekursionsgleichung für quickSort:
Die ist fast dieselbe Rekursionsgleichung wie für MergeSort und es folgt
Doch was ist, wenn die Voraussetzung des Theorems nicht erfüllt ist und wir ungleiche Rekursionsaufrufe haben?
Theorem der Laufzeit 2
BearbeitenDas Theorem der Laufzeit besagt, dass der Algorithmus quickSort im schlechtesten Fall eine Laufzeit von hat.
Beweis
BearbeitenAngenommen, die Aufteilung erzeugt ein Teilarray mit Länge n‐1 und ein Teilarray mit Länge 0 (Pivot‐Element ist also immer Minimum oder Maximum), dann erhalten wir folgende Rekursionsgleichung für die Laufzeit:
Durch Induktionsbeweis kann leicht gezeigt werden, dass . Dies ist auch tatsächlich der schlechteste Fall.
Für den mittleren Fall kann gezeigt werden, dass quickSort einen Aufwand von hat (wie im besten Fall), die in versteckten Konstanten sind nur etwas größer.
Bemerkung
BearbeitenIm Gegensatz zu MergeSort ist QuickSort durch die Vorgehensweise bei Vertauschungen instabil, d.h. relative Reihenfolge gleicher Schlüssel werden nicht notwendigerweise beibehalten.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.6 zu finden.
Untere Schranke
BearbeitenAuf dieser Seite wird die untere Schranke für vergleichbare Sortierverfahren behandelt.
Eigenschaften der betrachteten Algorithmen
BearbeitenDie Komplexität im Durchschnittsfall und im Schlechtesten Fall ist nie besser als n ‧ log n. Die Sortierung erfolgt ausschließlich durch Vergleich der Eingabe-Elemente (comparison sorts), es handelt sich somit um vergleichsorientierte Sortierverfahren. Nun zeigen wir, dass n ‧ log n Vergleiche eine untere Schranke für „Comparison Sort“-Algorithmen ist. Dies heißt dann, dass Sortieralgorithmen mit Komplexität (schlechtester Fall) von n ‧ log n (z.B. MergeSort) asymptotisch optimal sind.
Problembeschreibung
BearbeitenZuerst die Problembeschreibung. Als Eingabe haben wir . Als Vergleichstests nehmen wir . Als vereinfachte Annahmen nehmen wir an, dass es nur verschiedene Elemente gibt, somit entfällt . Die restlichen Test liefern alle gleichwertige Informationen. Sie bestimmen die Reihenfolge von . Außerdem können sie und auf beschränken. Somit haben wir eine binäre Entscheidung und es gilt entweder
Entscheidungsbaum
Bearbeiten
Eine beispielhafte Eingabe ist Die inneren Knoten vergleichen die Elemente . Es wird ein Test durchgeführt ob gilt oder nicht. Die Blätter sind Permutationen mit Sortieren heißt das Finden eines Pfades von der Wurzel zu einem Blatt. An jedem internen Knoten erfolgt ein Vergleich und entsprechend wird links oder rechts weiter gesucht. Ist ein Blatt erreicht, dann hat der Sortieralgorithmus eine Ordnung und die Permutation der Elemente ist erstellt. Daraus lässt sich schlussfolgern, dass jeder Sortieralgorithmus jede Permutation der n Eingabe-Elemente erreichen muss (n!). Daraus folgt wiederum, dass es n! Blätter geben muss, die alle von der Wurzel erreichbar sind. Andernfalls kann er zwei unterschiedliche Eingaben nicht unterscheiden und liefert für beide dasselbe Ergebnis und eins davon muss falsch klassifiziert sein. Die Anzahl an Vergleichen im schlechtesten Fall ist die Pfadlänge von Wurzel bis Blatt, oder auch Höhe genannt.
Somit erhalten wir das Theorem, dass jeder vergleichsorientierte Sortieralgorithmus im schlechtesten Fall mindestens n*log n Versuche braucht.
Beweis
BearbeitenGegeben ist die Anzahl der Elemente n, h die Pfadlänge bzw. Höhe des Baums und b die Anzahl der Blätter. Jede Permutation muss in einem Blatt sein, das bedeutet . Der Binärbaum hat die Höhe h und maximal Blätter, daraus folgt . Wenn man nun logarithmiert, erhält man
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.7 zu finden.
Dynamische Datenstrukturen
BearbeitenAuf dieser Seite wird es eine Einführung in die dynamischen Datenstrukturen geben. Unter dynamischen Datenstrukturen verstehen wir Datenstrukturen bei denen man Elemente löschen und hinzufügen kann, eine interne Ordnung (z.B. Sortierung) vorliegt und diese Ordnung unter Änderungen aufrecht erhalten bleibt. Ein Beispiel sind Lineare Datenstrukturen und Sortierung. Bei unsortierte Liste sind Änderung einfach, aber Zugriff aufwändig. Bei einer Neusortierung einer Liste sind Änderung schwierig, aber Zugriff einfach. Bei Trade-of ist eine “intelligente Datenstruktur” gesucht, die Änderungen und Zugriffe einfach, sprich effizient, halten. Viele dynamische Datenstrukturen nutzen Bäume als Repräsentation.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8.5 zu finden.
Bäume
BearbeitenIn diesem Kapitel werden Bäume als kurzen Einschub behandelt. Ein Baumelement e ist ein Tupel mit v vom Wert e und sind die Nachfolger, bzw. Kinder von e. Ein Baum T ist ein Tupel mit r als Wurzelknoten (ein Baumelement) und als Knoten (Baumelemente) des Baumes mit und für alle
Man spricht von einem geordneten Baum, wenn die Reihenfolge der Kinder eines jeden Elements festgelegt ist (schreibe dann statt
Beispiel
Bearbeiten
T' ist kein Baum, da ein gemeinsames Kind haben.
Begriffe
BearbeitenEin Pfad folgt über Kanten zu verbundenen Knoten, dabei existiert zu jedem Knoten genau ein Pfad von der Wurzel. Ein Baum ist immer zusammenhängend und zyklenfrei.
Das Niveau der jeweiligen Ebene entspricht immer der jeweiligen Länge des Pfades. Die Höhe eines Baumes entspricht dem größten Niveau+1.
Anwendungen
BearbeitenMan benutzt Bäume beispielsweise zur Darstellung von Hierarchien, wie Taxonomien, oder für Entscheidungsbäume. Bäume werden oft genutzt um sortierte, dynamische oder lineare Datenstrukturen zu repräsentieren, da Einfüge-und Löschoperationen leicht so definiert werden können, dass die Sortierung beibehalten wird. Ein Baum kann auch als Datenindex genutzt werden und stellt so eine Alternative zu Listen und Arrays dar.
Hier wird beispielsweise nach der 5 gesucht und der Baum wird als Suchbaum genutzt.
Man kann auch einen Baum aus Termen bilden. Der Term (3+4) * 5 + 2 * 3 gibt folgenden Baum:
Atomare Operationen auf Bäumen
BearbeitenZu den Operationen zählen lesen mit
- root(): Wurzelknoten eines Baums
- get(e): Wert eines Baumelements e
- children(e): Kinderknoten eines Elements e
- parent(e): Elternknoten eines Elements e
und schreiben mit
- set(e,v): Wert des Elements e auf v setzen
- addChild(e,e’): Füge Element e’ als Kind von e ein (falls geordneter Baum nutze addChild(e,e’,i) für Index i)
- del(e): Lösche Element e (nur wenn e keine Kinder hat)
Spezialfall: Binärer Baum als Datentyp
Bearbeiten
class TreeNode<K extends Comparable<K>>{
K key;
TreeNode<K> left = null;
TreeNode<K> right = null;
public TreeNode(K e) {key = e; }
public TreeNode<K> getLeft() {return left; }
public TreeNode<K> getRight() {return right; }
public K getKey() {return key; }
public void setLeft(TreeNode<K> n) {left = n;}
public void setRight(TreeNode<K> n) {right = n;}
...
}
Beispiel
BearbeitenTreeNode<Character> root = new TreeNode<Character>(‘A‘);
TreeNode<Character> node1 = new TreeNode<Character>(‘B‘);
TreeNode<Character> node2 = new TreeNode<Character>(‘C‘);
TreeNode<Character> node3 = new TreeNode<Character>(‘D‘);
root.setLeft(node1);
root.setRight(node2);
node2.setLeft(node3);
Typische Problemstellungen
BearbeitenAls typische Problemstellung haben wir zum einen die Traversierung, zum Anderen das Löschen eines inneren Knotens und die daraus folgende Re-strukturierung des Baumes und das Suchen in Bäumen.
Traversierung
BearbeitenBäume können visuell gut dargestellt werden. Manchmal ist jedoch eine Serialisierung der Elemente eines Baumes nötig. Man kann die Elemente eines Baumes durch Preorder-Aufzählung, Inorder-Aufzählung, Postorder-Aufzählung oder Levelorder-Aufzählung eindeutig aufzählen.
Bei der Traversierung werden systematisch alle Knoten des Baumes durchlaufen.
Preorder (W-L-R):
Inorder (L-W-R):
Postorder (L-R-W):
Levelorder:
Traversierung mit Iteratoren
BearbeitenBei der Traversierung sind Iteratoren erlaubt. Diese werden schrittweise abgearbeitet und es werden Standardschleifen für die Baumdurchläufe verwendet.
for (Integer i : tree)
System.out.print(i);
Dabei ist es allerdings notwendig, dass der Bearbeitungszustand zwischengespeichert wird.
public class BinarySearchTree<K extends Comparable<K>>
implement Iterable<K> {
public static final int INORDER = 1;
public static final int PREORDER = 2;
public static final int POSTORDER = 3;
public static final int LEVELORDER = 4;
private int iteratorOrder;
...
public void setIterationOrder(int io) {
if (io < i || io > 4)
return;
iteratorOrder = io;
}
public Iterator<K> iterator() {
switch (iterationOrder) {
case INORDER:
return new InorderIterator<K>(this);
case PRORDER:
return new PreorderIterator<K>(this);
case POSTORDER:
return new PostorderIterator<K>(this);
case LEVELORDER:
return new LevelorderIterator<K>(this);
default:
return new InorderIterator<K>(this);
}
}
Preorder Traversierung
BearbeitenBei der Preorder Traversierung wird der aktuelle Knoten zuerst behandelt und dann der linke oder rechte Teilbaum.
static class TreeNode<K extends Comparable<K>> {
...
public void traverse() {
if (key==null)
return;
System.out.print(” ” + key);
left.traverse();
right.traverse();
}
Preorder Iteratoren
BearbeitenDer Wurzelknoten wird auf den Stack gelegt, anschließend der rechte Knoten und dann der linke Knoten.
class PreorderIterator<K extends Comparable <K>>
implements Iterator<K> {
java.util.Stack<TreeNode<K>> st =
new java.util.Stack<TreeNode<K>>();
public PreorderIterator(BinarySearchTree<K> tree){
if (tree.head.getRight() != nullNode)
st.push(tree.head.getRight());
}
public boolean hasNext() {
return !st.isEmpty();
}
public K next(){
TreeNode<K> node = st.pop();
K obj = node.getKey();
node = node.getRight();
if(node != nullNode) {
st.push(node); //rechten Knoten auf den Stack
}
node = node.getLeft();
if(node != nullNode) {
st.push(node); //linken Knoten auf den Stack
}
return obj;
}
}
Inorder Traversierung
BearbeitenBei der Inorder Traversierung wird zuerst der linke Teilbaum behandelt, dann der aktuelle Knoten und dann der rechte Teilbaum. Als Ergebnis erhält man den Baum in sortierter Reihenfolge.
static class TreeNode<K extends Comparable<K>> {
...
public void traverse() {
if (key==null)
return;
left.traverse();
System.out.print(” ” + key);
right.traverse();
}
Inorder Iteratoren
BearbeitenDer Knoten head hat immer einen rechten Nachfolger. Es wird vom Wurzelknoten begonnen alle linken Knoten auf den Stack zu legen.
class InorderIterator<K extends Comparable <K>>
implements Iterator<K> {
java.util.Stack<TreeNode<K>> st =
new java.util.Stack<TreeNode<K>>();
public InorderIterator(BinarySearchTree<K> tree) {
TreeNode<K> node = tree.head.getRight();
while (node != nullNode) {
st.push(node);
node = node.getLeft();
}
}
public boolean hasNext() {
return !st.isEmpty();
}
public K next(){
TreeNode<K> node = st.pop();
K obj = node.getKey();
node = node.getRight(); //rechten Knoten holen
while (node != nullNode) {
st.push(node);
node = node.getLeft(); //linken Knoten auf den Stack
}
return obj;
}
}
Postorder Traversierung
BearbeitenBei der Postorder Traversierung wird zuerst der linke und der rechte Teilbaum behandelt und dann der aktuelle Knoten. Dies kann beispielsweise genutzt werden, um einen Baum aus Termen, entsprechend der Priorität der Operatoren, auszuwerten.
static class TreeNode<K extends Comparable<K>> {
...
public void traverse() {
if (key==null)
return;
left.traverse();
right.traverse();
System.out.print(” ” + key);
}
Levelorder Iteratoren
BearbeitenDer Wurzelknoten wird in der Warteschlange eingefügt. Dann wird zuerst der linke und dann der rechte Knoten in die Warteschlange eingefügt. In dieser Implementierung wird die queue als LinkedList repräsentiert. Dies ist jedoch beliebig.
class LevelorderIterator<K extends Comparable <K>>
implements Iterator<K> {
//Wurzelknoten in die Warteschlange (queue) einfügen
java.util.Queue<TreeNode<K>> q =
new java.util.LinkedList<TreeNode<K>>();
public LevelorderIterator(BinarySearchTree<K> tree){
TreeNode<K> node = tree.head.getRight();
if (node != nullNode)
q.addLast(node);}
public K next(){
TreeNode<K> node = q.getFirst();
K obj = node.getKey();
if (node.getLeft() != nullNode)
q.addLast(node.getLeft());
if (node.getRight() != nullNode)
q.addLast(node.getRight());
return obj;
}
}
Bäume in Java
BearbeitenIn Java gibt es keine hauseigene Implementierung für allgemeine Bäume. Einige Klassen (TreeMap, TreeSet) benutzen Bäume zur Realisierung anderer Datenstrukturen. Andere Klassen (JTree) benutzen Bäume als Datenmodell zur Visualisierung.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14 zu finden.
Binäre Suchbäume
BearbeitenAuf dieser Seite werden die binären Suchbäume behandelt. Er ermöglicht einen schneller Zugriff auf Daten mit dem Aufwand O(log n) unter geeigneten Voraussetzungen. Des weiteren ermöglicht er effiziente Sortierung von Daten, durch Heapsort und effiziente Warteschlangen. Der binäre Suchbaum dient als Datenstruktur für kontextfreie Sprachen. In der Computergrafik sind Szenengraphen oft (Beinahe-)Bäume. Bei Informationssysteme dienen binäre Suchbäume zur Datenindizierung und Anfrageoptimierung.
Operationen
BearbeitenAuf Suchbäumen können die Operationen Suchen von Elementen, Einfügen von Elementen und Entfernen von Elementen angewandt werden, wobei letztere zwei voraussetzen, dass die Ordnung der Schlüssel erhalten bleibt.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14 zu finden.
Suchen
BearbeitenEin binärer Suchbaum kann für viele Anwendungen eingesetzt werden.
Hier ist der Baum ein Datenindex und eine Alternative zu Listen und Arrays. Beispielsweise kann dieser Baum als Suchbaum verwendet werden und nach "5" gesucht werden.
Bei der Anwendung von Bäumen zur effizienten Suche gibt es pro Knoten einen Schlüssel und ein Datenelement und die Ordnung der Knoten erfolgt anhand der Schlüssel. Bei einem binärer Suchbaum enthält der Knoten k einen Schlüsselwert k.key. Alle Schlüsselwerte im linken Teilbaum k.left sind kleiner als k.key und alle Schlüsselwerte im rechten Teilbaum k.right sind größer als k.key. Die Auswertung eines Suchbaums sieht wie folgt aus:
- Vergleich des Suchschlüssels mit Schlüssel der Wurzel
- Wenn kleiner, dann in linken Teilbaum weiter suchen
- Wenn größer, dann in rechtem Teilbaum weiter suchen
- Sonst gefunden/nicht gefunden
static class TreeNode<K extends Comparable<K>>{
K key;
TreeNode<K> left = null;
TreeNode<K> right = null;
public TreeNode(K e) {key = e; }
public TreeNode<K> getLeft() {return left; }
public TreeNode<K> getRight() {return right; }
public K getKey() {return key; }
public void setLeft(TreeNode<K> n) {left = n;}
public void setRight(TreeNode<K> n) {right = n;}
...
}
Knotenvergleich
Bearbeitenclass TreeNode<...> {
...
public int compareKeyTo(K k) {
return (key == null ? -1:
key.compareTo(k));
}
...
}
Rekursives Suchen
Bearbeitenprotected TreeNode<K>
recursiveFindNode(TreeNode<K> n, k){
/* k wird gesucht */
if (n!= nullNode) {
int cmp = n.compareKeyTo(k.key);
if (cmp == 0)
return n;
else if (cmp > 0)
return
recursiveFindNode(n.getLeft(),k);
else
return
recursiveFindNode(n.getRight(),k);
}
else
return null;
}
Iteratives Suchen
Bearbeitenprotected TreeNode<K> iterativeFindNode(TreeNode<K> k){
/* k wird gesucht */
TreeNode<K> n = head.getRight();
while (n!= nullNode) {
int cmp = n.compareKeyTo(k.key);
if (cmp == 0)
return n;
else
n = (cmp > 0 ?
n.getLeft(): n.getRight());
}
return null;
}
Suchen des kleinsten Elements
Bearbeitenprotected K findMinElement(){
TreeNode<K> n = head.getRight();
while (n.getLeft() != nullNode)
n = n.getLeft();
return n.getKey();
}
Suchen des größten Elements
Bearbeitenprotected K findMaxElement(){
TreeNode<K> n = head.getRight();
while (n.getRight() != nullNode)
n = n.getRight();
return n.getKey();
}
Eine weitere Anwendungsmöglichkeit ist der Baum aus Termen. Wir haben den Term als Baumdarstellung sieht es so aus:
Bei der Auswertung müssen die Operatoren auf die beiden Werte der Teilbäume angewandt werden.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3 zu finden.
Einfügen
BearbeitenDas Finden der Einfügeposition erfolgt durch Suchen des Knotens, dessen Schlüsselwert größer als der einzufügende Schlüssel ist und der keinen linken Nachfolger hat oder durch Suchen des Knotens, dessen Schlüsselwert kleiner als der einzufügende Schlüssel ist und der keinen rechten Nachfolger hat. Das Einfügen erfolgt prinzipiell in 2 Schritten. Im ersten Schritt wird die Einfügeposition gesucht, sprich der Blattknoten mit dem nächstkleineren oder nächstgrößerem Schlüssel. Im zweiten Schritt wird ein neuer Knoten erzeugt und als Kindknoten des Knotens aus Schritt eins verlinkt. Wenn in Schritt eins der Schlüssel bereits existiert, dann wird nicht erneut eingefügt.
Programm in Java
Bearbeiten /* Einfügeposition suchen */
public boolean insert(K k){
TreeNode<K> parent = head;
TreeNode<K> child = head.getRight();
while (child != nullNode) {
parent = child;
int cmp = child.compareKeyTo(k);
//Schlüssel bereits vorhanden
if (cmp == 0)
return false;
else if (cmp > 0)
child = child.getLeft();
else
child = child.getRight();
}
/* Neuen Knoten verlinken */
TreeNode<K> node = new TreeNode<K>(k);
node.setLeft(nullNode);
node.setRight(nullNode);
if (parent.compareKeyTo(k) > 0)
parent.setLeft(node);
else
parent.setRight(node);
return true;
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3.2 zu finden.
Löschen
BearbeitenZuerst wird das zu löschendes Element gesucht, der Knoten k. Nun gibt es drei Fälle
- k ist Blatt: löschen
- k hat ein Kind: Kind „hochziehen“
- k hat zwei Kinder: Tausche mit weitest links stehenden Kind des rechten Teilbaums, da dieser in der Sortierreihenfolge der nächste Knoten ist und entferne diesen nach den Regeln 1. oder 2.
Ein Schlüssel wird in drei Schritten gelöscht. Im ersten Schritt wird der zu löschende Knoten gefunden. Im zweiten Schritt wird der Nachrückknoten gefunden. Dafür gibt es mehrere Fälle. Im Fall 1 handelt es sich um einen externen Knoten, sprich ein Blatt, ohne Kinder. Dabei wird der Knoten durch einen nullNode ersetzt. Im Fall 2a gibt es nur einen rechten Kindknoten, dabei wird der gelöschte Knoten durch den rechten Kindknoten ersetzt. Im Fall 2b gibt es nur einen linken Kindknoten und der gelöschte Knoten wird durch diesen ersetzt. Im Fall 3 gibt es einen internen Knoten mit Kindern rechts und links. Dabei wird der gelöschte Knoten durch den Knoten mit dem kleinstem (alternativ größtem) Schlüssel im rechten (alternativ linken) Teilbaum ersetzt. im dritten und letzten Schritt wird nun der Baum reorganisiert. Während dem Löschen kann sich die Höhe von Teilbäumen ändern.
Programm in Java
Bearbeiten /* Knoten suchen */
public boolean remove(K k){
TreeNode<K> parent = head;
TreeNode<K> node = head.getRight();
TreeNode<K> child = null;
TreeNode<K> tmp = null;
while (node != nullNode) {
int cmp = node.compareKeyTo(k);
//Löschposition gefunden
if (cmp == 0)
break;
else {
parent = node;
node = (cmp > 0 ?
node.getLeft() : node.getRight());
}
}
//Knoten k nicht im Baum
if (node == nullNode)
return false;
/* Nachrücker finden */
if (node.getLeft() == nullNode &&
Node.getRight() == nullNode) //Fall 1
child = nullNode;
else if (node.getLeft() == nullNode) //Fall 2a
child = node.getRight();
else if (node.getRight() == nullNode) //Fall 2b
child = node.getLight();
...
//Fall 3
else {
child = node.getRight();
tmp = node;
while (child.getLeft() != nullNode) {
tmp = child;
child = child.getLeft();
}
child.setLeft(node.getLeft());
if (tmp != node) {
tmp.setLeft(child.getRight());
child.setRight(node.getRight());
}
}
/* Baum reorganisieren */
if (parent.getLeft() == node)
parent.setLeft(child)
else
parent.setRight(child);
return true;
...
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3.2 zu finden.
Implementierung
BearbeitenEin binärer Suchbaum ist eine häufig verwendete Hauptspeicherstruktur und ist besonders geeignet für Schlüssel fester Größe, z.B. numerische wie int, float und char[n]. Der Aufwand von O(log n) für Suchen, Einfügen und Löschen ist garantiert, vorausgesetzt der Baum ist balanciert. Später werden wir lernen, dass die Gewährleistung der Balancierung durch spezielle Algorithmen gesichert wird. Des weiteren sind größere, angepasste Knoten für Sekundärspeicher günstiger, diese nennt man B-Bäume. Für Zeichenketten benutzt man als Schlüssel variable Schlüsselgröße, sogenannte Tries.
public class
BinarySearchTree<K extends Comparable<K>>
implements Iterable<K> {
...
static class TreeNode<K extends Comparable<K>> {
K key;
TreeNode<K> left = null;
TreeNode<K> right = null;
...
}
}
Die Schlüssel müssen Comparable-Interface, d.h. compareTo()-Methode, implementieren, da der Suchbaum auf Vergleichen der Schlüssel basiert. Der Baum selbst implementiert Iterable-Interface, d.h. iterator()-Methode, um Traversierung des Baums über Iterator zu erlauben (später Baumtraversierung).TreeNode und alles weitere werden als innere Klassen implementiert. Dadurch werden Zugriff auf Attribute und Methoden der Baumklasse erlaubt. Eine Besonderheit der Implementierung sind die „leeren“ Pseudoknoten head und nullNode zur Vereinfachung der Algorithmen (manchmal „Wächter“ / „sentinel“ genannt). Grundlegende Algorithmen sind
- Suchen
- Einfügen
- Löschen
Implementierung mit Pseudoknoten
BearbeitenWir vereinbaren an dieser Stelle, dass man auf dem Kopf kein getRight() anwenden kann.
public class
BinarySearchTree<K extends Comparable<K>>
implements Iterable<K> {
...
pulic BinarySearchTree(){
head = new TreeNode<K>(null);
nullNode = new TreeNode<K>(null);
nullNode.setLeft(nullNode);
nullNode.setRight(nullNode);
head.setRight(nullNode);
}
...
}
Das Ziel der Implementierung ist, die Reduzierung der Zahl an Sonderfällen. Im head würde das Einfügen oder Löschen des Wurzelknotens spezielle Behandlung in der Baum-Klasse erfordern. Der nullNode erspart den Test, ob zum linken oder zum rechten Teilknoten navigiert werden kann. Des weiteren ist im NullNode ein einfaches Beenden der Navigation (z.B. Beenden der Rekursion) möglich.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.2.1 zu finden.
Weitere Aspekte
BearbeitenDie Komplexität der Operation hängt von der Höhe ab. Der Aufwand für die Höhe des Baumes beträgt O(h). Die Höhe eines ausgeglichenen binären Baumes ist h=ld(n) für Knoten. Bei eines ausgeglichenen oder balancierten Baum unterscheiden sich zum einen der rechte und linke Teilbaum eines jeden Knotens in der Höhe um höchstens 1 und zum anderen unterscheiden sich je zwei Wege von der Wurzel zu einem Blattknoten höchstens in um 1 in der Länge. Rot-Schwarz Bäume und AVL Bäume benötigen einen Ausgleich nach dem Einfügen und Löschen.
Entartung von Bäumen
BearbeitenUngünstige Einfüge- oder Löschreihenfolge führt zu extremer Unbalanciertheit. Im Extremfall wird der Baum zur Liste, dann haben die Operationen eine Komplexität von O(n). Beispiel:
for (int i = 0; i < 10; i++) tree.insert(i);
Vermeiden kann man dies durch spezielle Algorithmen zum Einfügen und Löschen, z.B. mit Rot-Schwarz-Bäumen und AVL-Bäumen.
Heaps
BearbeitenHeap Sort
BearbeitenAuf dieser Seite wird das Thema Heap Sort behandelt. Von "Heap" gibt es zwei völlig verschiedene Definitionen. Zum einen ist es ein größeres Gebiet im Hauptspeicher, aus dem Programmierer Blöcke beanspruchen und wieder freigeben können und zum anderen ist es ein balancierter, linksbündiger Binärbaum in dem kein Knoten einen Wert hat, der größer ist als der Wert seines Elternknoten. Im Falle von Heapsort wird die zweite Definition benutzt.
Balancierter Binärbaum
BearbeitenJeder Knoten ist in einer Ebene platziert, der Wurzelknoten in Ebene 0. Die Höhe eines Baumes ist die Distanz von seiner Wurzel zum weitest entfernten Knoten plus 1. Ein Knoten ist tiefer als ein anderer Knoten, wenn seine Ebene eine höhere Zahl hat. Ein Binärbaum der Höhe h ist balanciert, wenn alle Knoten der Ebenen 0 bis h-3 zwei Kinder haben.
Ein balancierter Binärbaum der Höhe h ist linksbündig, wenn er Knoten in der Ebene k hat für alle und alle Blätter der Ebene h-1 so weit wie möglich links sind.
Motivation
BearbeitenDer Vorteil von MergeSort gegenüber QuickSort ist, dass MergeSort einen garantierten Aufwand von O(n log n) hat. Der Vorteil von QuickSort gegenüber MergeSort ist, dass QuickSort n viel Speicher benötigt und MergeSort 2n viel Speicher. Gibt es nun einen Sortieralgorithmus, der n viel Speicher benötigt und garantiert in O(n log n) läuft? Ja HeapSort! Mit HeapSort lassen sich zudem die Warteschlangen mit Prioritäten effizient implementieren. Außerdem ist die Idee des Heaps sehr interessant. Eine komplexe Datenstruktur (Baum) wird in einer einfacheren Struktur (Array) abgebildet.
Heap Eigenschaft
BearbeitenEin Knoten hat die Heap-Eigenschaft, wenn der Wert in dem Knoten so groß oder größer ist als die Werte seiner Kinder. Alle Blattknoten haben dann auch automatisch die Heap Eigenschaft. Ein Binärbaum ist nur dann ein Heap, wenn alle Knoten die Heap Eigenschaft besitzen.
Anmerkung
BearbeitenEin Heap ist kein binärer Suchbaum. Das Sortierkriterium bei Suchbäumen war, dass der Wert eines Knotens stets größer ist, als die Werte der Knoten, die im linken Teilbaum liegen und, dass der Wert eines Knotens stets kleiner ist, als die Werte der Knoten, die im rechten Teilbaum liegen. Das Sortierkriterium beim Heap ist, dass die Werte eines Knotens stets größer oder gleich der Werte der Knoten sind, die in beiden Teilbäumen liegen.
Literatur
BearbeitenDa die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.6.1 zu finden.
Hashtabellen
BearbeitenHashtabellen
BearbeitenAuf dieser Seite wird das Thema Hashtabellen behandelt. Gesucht ist eine dynamische Datenstruktur mit sehr schnellem direktem Zugriff auf Elemente. Die Idee der Hashfunktion ist, dass ein Feld von 0 bis N-1 benutzt wird, beispielsweise ein Array. Die einzelnen Positionen im Feld werden oft als Buckets bezeichnet. Die Hashfunktion h(e) bestimmt für Elemente e die Position im Feld. H(e) ist sehr schnell berechenbar. Es gilt
Beispiele
BearbeitenWir haben ein Array von 0 bis 9 und h(i)=i mod 10. Das Array sieht nach dem Einfügen der Zahlen 42 und 119 wie folgt aus:
| Index | Eintrag |
| 0 | |
| 1 | |
| 2 | 42 |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | 119 |
Der Vorteil von Hashing ist, dass Anfragen der Form " Enthält die Datenstruktur das Element 42?" schnell beantwortbar sind. Dazu verhalten sich Hashtabellen ähnlich zu binären Suchbäumen wie BucketSort zu vergleichsbasierten Sortierverfahren.
Hashfunktionen
BearbeitenDie Hashfunktionen hängen vom Datentyp der Elemente und der konkreten Anwendungen ab. Für den Datentyp Integer ist die Hashfunktion meist h(i)=i mod N. Das funktioniert im Allgemeinen sehr gut, wenn N eine Primzahl ist und hängt mit Methoden zur Erzeugung von Zufallszahlen zusammen. Für andere Datentypen führt man eine Rückführung auf Integer aus. Bei Fließpunkt-Zahlen werden Mantisse und Exponent einfach addiert.
Die Hashwerte sollten gut streuen. Das ist eventuell von den Besonderheiten der Eingabewerte abhängig. Beispielsweise tauchen Buchstaben des Alphabets in Namen unterschiedlich oft auf.
Des weiteren müssen die Hash-Werte effizient berechenbar sein. Ein konstanter Zeitbedarf ist erfordert, dieser ist nicht von der Anzahl der gespeicherten Werte abhängig.
Ungünstige Hashfunktionen
BearbeitenAls erstes Beispiel wählen wir und eine generierte Artikelnummer mit den Kontrollziffern 1,3 oder 7 am Ende. Damit wäre die Abbildung nur auf ungeraden Adressen möglich. Als zweites Beispiel wählen wir Matrikelnummern in einer Hashtabelle mit 100 Einträgen. In der ersten Variante nutzen wir die ersten beiden Stellen als Hashwert, damit kann eine Abbildung nur auf wenige Buckets erfolgen. In der zweiten Variante nutzen wir die beiden letzten Stellen und erhalten eine gleichmäßige Verteilung.
Typen von Graphen und Anwendungen
BearbeitenIn diesem Kapitel werden Graphen behandelt. Ein Graph ist das mathematische Modell eines Netzwerks bestehend aus Knoten und Kanten. Graphen haben einen vielfältigen Einsatz. So kommen sie bei Verbindungsnetzwerken (Bahnnetz, Flugververbindungen, Straßenkarten, ...), Verweisen (WWW, Literaturverweise, Wikipedia, symbolische Links, ...), Technischen Modellen (Platinen-layout, finite Elemente, Computergrafik) und Software Reengineering und - dokumentation zum Einsatz. Bäume und Listen sind spezielle Graphen.
Ungerichteter Graph
BearbeitenEs gibt verschiedene Typen von Graphen. Der ungerichtete Graph ist beispielsweise eine Straßenverbindung, eine Telefonnetz oder ein soziales Netzwerk. Ein ungerichteter Graph ist ein Tupel G=(V,E). Wir haben eine endliche Menge V von Knoten (Vertices) und eine Menge E von Kanten (Edges), die aus ungeordneten Paaren aus V besteht. Es gilt, dass und jedes ist eine zweielementige Teilmenge der Knotenmenge . Im ungerichteten Graphen gibt es keine Schleifen, das heißt es gibt keine Kanten die von einem Knoten zu sich selbst laufen. Außerdem gibt es keine mehrfachen Kanten zwischen zwei Knoten, Parallelkanten genannt.
Hier können zum Beispiel die kürzesten Wege bei sozialen Netzwerken wie Facebook berechnet werden.
Spezielle Graphen
BearbeitenSei ein Graph.
G heißt planar, falls er ohne Überschneidungen der Kanten in der Ebene gezeichnet werden kann.
G heißt vollständig, falls
G heißt regulär, falls alle Knoten denselben Grad haben
G heißt bipartit, falls und
- keine zwei Knoten in sind adjazent
- keine zwei Knoten in sind adjazent
Beispiele
BearbeitenDieser Graph ist sowohl planar, regulär als auch vollständig.

Dieser Graph ist jedoch nur regulär und vollständig.

Hier handelt es sich nur um einen regulären Graphen.

Dies ist ein Beispiel für einen bipartiten Graph.

Gerichteter Graph
BearbeitenDer gerichtete Graph ist beispielsweise eine Förderanlage oder ein Kontrollfluss in Programmen. Der gerichtete Graph (auch Digraph) ist ein Tupel G=(V,E) mit V als endliche Menge von Knoten und E einer Menge von Kanten, geordneten Paaren aus V. Jedes ist nun ein Tupel e=(a,b) mit . Schleifen der Form (a,a) sind nun erlaubt. Dazu ist (a,b) eine andere Kante als (b,a). Der Unterschied zwischen (a,b) und {a,b} besteht darin, dass das Tupel (a,b) geordnet ist. Die Reihenfolge kann nicht verändert werden. Hingegen ist {a,b} eine Menge, in der die Reihenfolge der Elemente keine Rolle spielt.
Gerichtete Graphen werden zum Beispiel als Web-Graph (Google`s PageRank) benutzt. Aber auch in der Scientometrie kommen sie zum Einsatz bei der Impact Faktoren Berechnung. Bei Datenstrukturen im Semantik Web werden gerichtete Graphen zum Speichern von Daten genutzt.
Gerichtete und ungerichtete Graphen
BearbeitenEin ungerichteter Graph kann in einen gerichteten Graphen transformiert werden, indem jede ungerichtete Kante {v,w} durch zwei gerichtete Kanten (v,w) und (w,v) ersetzt wird. Dann ist beispielsweise der Zusammenhang identisch mit dem starken Zusammenhang. Dazu haben gerichtete Graphen eine größere Ausdrucksstärke und daher wird "Graph" oft als Synonym für einen Digraph verwendet.
Gewichteter Graph
BearbeitenEin ungerichteter gewichteter Graph ist beispielsweise eine Flugverbindung mit Meilen oder Kosten, ein Straßennetz mit Kilometern oder ein Rohrsystem mit Durchfluss.
Ein gerichteter gewichteter Graph ist beispielsweise ein Straßennetz mit Einbahnstraßen, Rohre mit Ventilen oder ein Förderband.
Der Graph ist ein Paar G=(V,E) und wir haben eine Kantengewichtsfunktion g. Daraus erhalten wir G=(V,E,g) mit . Der Graph kann gerichtet oder ungerichtet sein und die Kantengewichte müssen nicht notwendigerweise natürliche Zahlen sein.
Ungerichtete gewichtete Graphen kommen zum Beispiel bei der Navigation beim Berechnen des kürzesten Weges zum Einsatz.
Gerichtete gewichtete Graphen kommen bei der Optimierung in der Telekommunikation zum Einsatz.
Hypergraph
BearbeitenEs gibt aber noch viele weitere Varianten von Graphen wie Multigraphen oder Hypergraphen.
Ein Hypergraph ist ein Paar G=(V,E) mit einer Menge von Knoten V und einer Menge von Hyperkanten .
Definitionen
BearbeitenHier werden allgemeine Definitionen bezüglich der Graphen behandelt. Dazu werden immer wieder Beispiele gebracht, die sich auf folgende Graphen beziehen. Dabei gilt je nach Beispiel G=(V,E) entweder für den ungerichteten oder den gerichteten Graphen.
Adjazenz
BearbeitenUngerichteter Graph
BearbeitenZwei Knoten heißen adjazent, falls .
Hier heißt v auch Nachbar von w.
Beispiel:
- Knoten 1 und 3 sind adjazent
Gerichteter Graph
BearbeitenZwei Knoten heißen adjazent, falls oder .
Für heißt w Nachfolger von v und v Vorgänger von w.
Beispiele:
- Knoten 1 ist Vorgänger zu Knoten 3
- Knoten 4 ist Nachfolger zu Knoten 6
Inzidenz
BearbeitenUngerichteter Graph
BearbeitenEine Kante ist inzident zu einem Knoten , falls oder .
Gerichteter Graph
BearbeitenEine Kante ist inzident zu einem Knoten , falls oder .
Grad
BearbeitenUngerichteter Graph
BearbeitenDer Grad (engl. degree) eines Knotens ist die Anzahl seiner inzidenten Kanten, das heißt: .
Beispiel:
- Der Grad von Knoten 4 ist 3
Gerichteter Graph
BearbeitenDer Eingangsgrad (engl. in-degree) eines Knotens ist die Anzahl seiner Vorgänger: .
Der Ausgangsgrad (engl. out-degree) eines Knotens ist die Anzahl seiner Nachfolger: .
Beispiele:
- Der Eingangsgrad von Knoten 3 ist 2
- Der Ausgangsgrad von Knoten 3 ist 3
Weg
BearbeitenUngerichteter Graph
BearbeitenEin Weg W ist eine Sequenz von Knoten mit für die gilt:
Beispiel:
- (1,3,5,6,3,4) ist ein Weg
Gerichteter Graph
BearbeitenEin (gerichteter) Weg W ist eine Sequenz von Knoten .
Beispiel:
- (1,3,6,5,5,3,1) ist ein (gerichteter) Weg
Pfad
BearbeitenEin Weg W heißt Pfad, falls zusätzlich gilt . Das heißt, der Weg enthält keine doppelten Knoten. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- (1,4,6,5) ist ein Pfad
Kreis
BearbeitenEin Weg P heißt Kreis, falls . Dazu ist ein Kreis K elementar, falls . Der Kreis enthält also keine doppelten Knoten bis auf den Anfangs- und den Endpunkt. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- (1,3,4,6,3,4,1) ist ein Kreis
- (3,4,6,3) ist ein elementarer Kreis
Länge
BearbeitenDie Länge eines Weges ist die Anzahl der durchlaufenen Kanten. Die Länge eines Pfades ist also n-1. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- Die Länge von (3,4,6,3,4,1) ist 4
- Die Länge von (1,3,6) ist 2
Teilgraph
BearbeitenUngerichteter Graph
BearbeitenEin Graph heißt Teilgraph von G, falls .
Beispiel:
- G'=({3,4,6},{{3,4},{4,6}}) ist ein Teilgraph von G
Gerichteter Graph
BearbeitenEin Graph heißt Teilgraph von G, falls und .
Beispiel:
- ist ein Teilgraph von .
Erreichbarkeit
BearbeitenUngerichteter Graph
BearbeitenEin Knoten heißt erreichbar von einem Knoten , falls ein Weg existiert mit und .
Beispiele:
- Knoten 6 ist erreichbar von Knoten 1
- Knoten 7 ist nicht erreichbar von Knoten 1
Gerichteter Graph
BearbeitenEin Knoten heißt erreichbar von einem Knoten , falls ein Weg existiert mit und .
Beispiele:
- Knoten 6 ist erreichbar von Knoten 1
- Knoten 5 ist nicht erreichbar von Knoten 2
Zusammenhang
BearbeitenUngerichteter Graph
BearbeitenG heißt (einfach) zusammenhängend, falls für alle gilt, dass w von v erreichbar ist
Ein Teilgraph von G heißt Zusammenhangskomponente von G, falls G' zusammenhängend ist und kein Teilgraph von G existert mit .
Beispiele:
- G ist nicht zusammenhängend
- Der Teilgraph ist eine Zusammenhangskomponente von G
- Der Teilgraph ist eine Zusammenhangskomponente von G
Gerichteter Graph
BearbeitenG heißt (stark) zusammenhängend, falls für alle gilt, dass w von v und v von w erreichbar ist.
Ein Teilgraph von G heißt starke Zusammenhangskomponente von G, falls stark zusammenhängend ist und kein Teilgraph von G existiert mit .
Beispiel:
- Der Teilgraph mit und ist eine starke Zusammenhangskomponente von .
Repräsentation von Graphen
BearbeitenAuf dieser Seite wird die Repräsentation von Graphen behandelt. Wir fragen uns wie effizient die Datenstruktur für Graphen ist.
Kanten- und Knotenlisten
BearbeitenBei durchnummerierten Knoten erfolgt eine einfache Realisierung. Historisch gesehen ist es die erste verwendete Datenstruktur. Außerdem ist sie als Austauschformat geeignet und die Auflistung ist nach Knoten oder nach Kanten sortiert.
Beispiel Kantenliste
Bearbeiten
Gegeben ist eine Kantenliste für
Die erste Zahl (6) steht für die Knotenzahl. Die zweite Zahl (11) steht für die Kantenzahl. Die weiteren Paare (1,2 ; 1,3...) stehen für die Kanten.
6,11,1,2,1,3,3,1,4,1,3,4,3,6,5,3,5,5,6,5,6,2,6,4
Beispiel Knotenliste
Bearbeiten
Gegeben ist eine Knotenliste für
6,11,2,2,3,0,3,1,4,6,1,1,2,3,5,3,2,4,5 Die Teilfolge 2,2,3 bedeutet, dass der Knoten 1 den Ausgangsgrad 2 hat und herausgehende Kanten zu den Knoten 2 und 3.
Vergleich Kanten-und Knotenliste
BearbeitenFalls ein Graph mehr Kanten als Knoten hat (=„Normalfall“),benötigen Knotenlisten weniger Speicherbedarf als Kantenlisten. Das bedeutet für die Kantenlisten gilt und für die Knotenliste gilt .
Adjazenzmatrix
BearbeitenAdjazenz bedeutet berühren oder aneinander grenzen. Hier werden die Graphen als Boole‘sche Matrix dargestellt. 1-Einträge werden für direkte Nachbarschaften verwendet. A ist eine Adjazenzmatrix für den Graph
Beispiel
Bearbeiten
Eigenschaften
BearbeitenBei ungerichteten Graphen reicht eine Halbmatrix (ein Dreieck) aus. Bei gewichteten Graphen werden Gewichte statt Boolsche Werte genutzt. Der Vorteil einer Adjazenzmatrix ist, dass einige Graphenoperationen als Matrixoperation möglich sind. So ist sie beispielsweise durch iterierte Matrixmultiplikation erreichbar und besitzt schöne Eigenschaften für die mathematische Analyse.
So sieht die Darstellung als Dreiecksmatrix aus. Die Diagonale kann ebenfalls weggelassen werden, wenn Schleifen verboten sind.
Adjazenzliste
BearbeitenWir haben eine Liste der 3b oder alternativ ein Array. Pro Knoten werden die von ihm ausgehenden Kanten als Liste, welche besonders geeignet für dünn besetzte Matrizen sind, oder als Array von Zeigern dargestellt. Der Graph wird durch |V|+1 verkettete Listen realisiert. In Adjazenzlisten sind dynamische Erweiterungen im Sinne verketteter Listen erlaubt. Knotenlisten können natürlich auch als verkettete Listen realisiert werden.

Speicherbedarf
BearbeitenSeien n=|V| und m=|E|. Benötigt werden insgesamt Listenelemente. ag(i) ist die Anzahl der Nachbarn von i (gerichtet).
Transformation zwischen den Darstellungen
BearbeitenDie vorgestellten Realisierungsvarianten sind äquivalent. Jede Darstellung kann in jede andere ohne Informationsverlust transformiert werden. Dafür wird die eigene Darstellung ausgelesen und anschließend die andere Darstellung erzeugt. Der Aufwand dieser Transformationen variiert von O(n+m) bis wobei im schlechtesten Fall gilt. tritt immer auf, wenn eine naive Matrixdarstellung beteiligt ist. Nicht naive Darstellungen sind für sehr dünn besetzte Matrizen nötig.
Komplexitätsbetrachtung
BearbeitenBei Kantenlisten ist das Einfügen von Kanten (Anhängen von zwei Zahlen) und von Knoten (Erhöhung der ersten Zahl um 1) besonders günstig. Das Löschen von Kanten zieht das Verschieben der nachfolgenden Kanten mit sich und die Knoten müssen neu nummeriert werden.
Bei Knotenlisten ist das Einfügen von Knoten, also die Erhöhung der ersten Zahl und das Anhängen einer 0, günstig.
Bei der Matrixdarstellung ist das Manipulieren von Kanten sehr effizient ausführbar. Der Aufwand beim Knoteneinfügen hängt von der Realisierung ab. Im worst case wird die Matrix in eine größere Matrix kopiert.
Bei Adjazenzlisten gibt es unterschiedlichen Aufwand, je nachdem, ob die Knotenliste ein Feld mit Direktzugriff oder eine verkettete Liste mit sequenziellem Durchlauf realisiert.
| Operation | Kantenliste | Knotenliste | Adjazenzmatrix | Adjazenzliste |
| Einfügen Kanten | Beta(1) | O(n+m) | O(1) | O(1)/O(n) |
| Löschen Kanten | O(m) | O(n+m) | O(1) | O(n) |
| Einfügen Knoten | O(1) | O(1) | O(1) | |
| Löschen Knoten | O(m) | O(n+m) | O(n+m) |
Das Löschen eines Knotens impliziert für gewöhnlich auch das Löschen der dazugehörigen Kanten.
Datenstrukturen für Graphen
BearbeitenAuf dieser Seite werden die Datenstrukturen für Graphen behandelt. In Java gibt es keine hauseigene Graphimplementierung, aber es gibt diverse Pakete für verschiedene Anwendungen.
- Jung (http://jung.sourceforge.net)
Graph<Integer, String> g = new SparseMultigraph<Integer, String>();
g.addVertex((Integer)1);
g.addVertex((Integer)2);
g.addEdge("Edge1", 1, 2);
- Neo4j (http://www.neo4j.org)
GraphDatabaseService= new
"GraphDatabaseFactory().newEmbeddedDatabase(“PATH”);
Transaction tx = graphDb.beginTx();
try{
Node firstNode = graphDb.createNode();
Node secondNode = graphDb.createNode();
Relationship relationship = firstNode.createRelationshipTo(secondNode,
… );
tx.success();
}finally{
tx.finish();
}
Die allgemeine Schnittstelle für die Vorlesung ist:
public interface Graph {
public int addNode();
public boolean addEdge (int orig, int dest);
}
Implementierung Adjazenzliste
Bearbeiten public class AdjazenzListGraph implements Graph {
private int [][] adjacencyList=null;
//Knoten hinzufügen:
public int addNode() {
int nodeNumber = (adjacencyList ==null)?0: adjacencyList.length;
int [][] newAdjacencyList= new int [nodeNumber+1][];
//alte adjacencyList kopieren
for (int i=0; i< nodeNumber; i++)
newAdjacencyList [i]=adjacencyList[i];
//neuer Knoten hat noch keine Kanten
newAdjacencyList[nodeNumber] =null;
adjacencyList=newAdjacencyList;
return nodeNumber+1;
}
//Kante hinzufügen:
public boolean addEdge (int orig, int dest){
int nodeNumber = (adjacencyList == null)? 0: adjacencyList.length;
if (orig > nodeNumber || dest > nodeNumber || orig < 1 || dest < 1 )
return false;
if (adjacencyList[orig-1] != null)
for (int n : adjacencyList[orig-1])
//Kante bereits vorhanden?
if (n==dest) return false;
//Erste Kante am Knoten orig?
if ( adjacencyList[orig-1] == null ) {
adjacencyList [orig-1] = new int[1];
adjacencyList[orig-1][0]=dest;
}
else {
int[] newList= new int[adjacencyList[orig-1].length+1];
System.arraycopy(adjacencyList[orig-1],0,newList,0,adjacencyList[orig-1].length);
newList[adjacencyList[orig-1].length]=dest;
adjacencyList [orig-1]=newList;
}
return true;
}
}
Breitensuche
BearbeitenAuf dieser Seite behandeln wir die Breitensuche. Wir fragen uns wie man die Knoten eines Graphen effizient aufzählt. Die Lösung ist der Breitendurchlauf ( Breadth-First-Search, BFS). Dabei werden die Knoten eines Graphen nach der Entfernung vom Zielknoten aufgezählt. Eine andere Methode ist der Tiefendurchlauf, zu dem kommen wir aber später. Bei dem Breitendurchlauf für ungerichtete Graphen gibt es eine Warteschlange als Zwischenspeicher. Farbmarkierungen beschreiben den Status der Knoten. Weiß bedeutet er ist unbearbeitet, grau bedeutet er ist in Bearbeitung und schwarz bedeutet, dass er abgearbeitet ist. Pro Knoten wird die Entfernung zum Startknoten berechnet. Bei der Initialisierung wird der Startknoten in eine Warteschlange eingefügt, die Farbe auf grau gesetzt und die Entfernung mit 0 berechnet. Die anderen Knoten haben eine unendliche Entfernung und sind weiß markiert.
Beim Breitendurchlauf wird der aktuelle Knoten k aus der Warteschlange genommen und schwarz gefärbt. Alle von k aus erreichbaren weißen Knoten werden grau gefärbt, die Entfernung ist der Entfernungswert von k+1 und sie werden in der Warteschlange aufgenommen.
Algorithmus
BearbeitenErgänzung zum Graph-Interface:
public interface Graph{
public int addNode();
public boolean addEdge(int orig, int dest);
public Collection<Integer> getChildren(int node);!
}
Breitendurchlauf als Iterator:
public class BfsIterator implements Iterator<Integer>{
private Graph g;
private Queue<Integer> q;
private Set<Integer> visited;
public BfsIterator(Graph g, int s){
this.g = g;
this.q = new LinkedList<Integer>();
q.add(s);
this.visited = new HashSet<Integer>();
}
public boolean hasNext() { return !this.q.isEmpty(); }
public Integer next() {
Integer n = this.q.poll();
for(Integer m: this.g.getChildren(n))
if(!this.visited.contains(m) && !this.q.contains(m))
this.q.add(m);
this.visited.add(n);
return n;
}
}
Ausgabe aller Knoten:
//Sei g ein Graph
Iterator<Integer> it = new BfsIterator(g,1);
while(it.hasNext())
System.out.println(it.next());
Analyse
BearbeitenTheorem der Terminierung
BearbeitenDie Breitensuche terminiert nach endlicher Zeit
Theorem der Korrektheit
BearbeitenIst G zusammenhängend, so werden alle Knoten von G genau einmal besucht.
Theorem der Laufzeit
BearbeitenIst G=(V,E) zusammenhängend und ist die Laufzeit von getChildren linear in der Anzahl der Kinder, so hat die Breitensuche eine Laufzeit von O(|V| + |E|).
Tiefendurchlauf
BearbeitenAuf dieser Seite wird der Tiefendurchlauf behandelt. Der Tiefendurchlauf wird auch Depth-First-Search, oder abgekürzt DFS, genannt. Die Knoten werden aufgezählt indem vom Startknoten aus ein Pfad so weit wie möglich verfolgt wird und bei Bedarf ein Backtracking durchgeführt wird. Bei Tiefendurchlauf werden die Knoten ebenfalls farblich markiert. Weiß bedeutet der Knoten ist noch nicht bearbeitet, grau bedeutet der Knoten ist in Bearbeitung und schwarz bedeutet der Knoten ist bereits fertig abgearbeitet.
Ergänzung zum Graph Interface:
public interface Graph{
public int addNode();
public boolean addEdge(int orig, int dest);
public Collection<Integer> getChildren(int node);
public Collection<Integer> getNodes();
}
Algorithmus
Bearbeitenenum Color {WHITE, GRAY, BLACK};
Map<Integer,Color> color = new HashMap<Integer,Color>();
Map<Integer,Integer> pi = new HashMap<Integer,Integer>();
Map<Integer,Integer> f = new HashMap<Integer,Integer>();
Map<Integer,Integer> d = new HashMap<Integer,Integer>();
int time = 0;
color speichert die Farbe, bzw. den Bearbeitungszustand eines Knotens.
pi speichert den Vorgänger eines Knotens beim Durchlauf.
f speichert den Zeitpunkt des Bearbeitungsbeginns eines Knotens.
d speichert den Zeitpunkt des Bearbeitungsendes eines Knotens.
public void dfs(Graph g){
for(Integer n: g.getNodes())
color.put(n, Color.WHITE);
for(Integer n: g.getNodes())
if(color.get(n).equals(Color.WHITE))
dfsVisit(g,n);
}
public void dfsVisit(Graph g, Integer n){
color.put(n, Color.GRAY);
time++;
d.put(n, time);
for(Integer m: g.getChildren(n)){
if(color.get(m).equals(Color.WHITE)){
pi.put(m, n);
dfsVisit(g,m);
}
}
color.put(n, Color.BLACK);
time++;
f.put(n, time);
}
Vorgehen
BearbeitenDer Tiefendurchlauf ist ein rekursiver Abstieg. Pro Knoten haben wir zwei Werte und deren Farbwerte. Beginn der Bearbeitung ist d und Ende der Bearbeitung ist f. Der rekursive Aufruf erfolgt nur bei weißen Knoten, die Terminierung der Rekursion ist hier garantiert. Die Ausführung von DFS resultiert in einer Folge von DFS-Bäumen. Der erste Baum wird aufgebaut bis keine Knoten mehr hinzugefügt werden können. Anschließend wird ein unbesuchter Knoten gewählt und fortgefahren. Bei den Kanten des aufgespannten Baumes ist der Zielknoten beim Test weiß. An den B-Kanten ist der Zielknoten beim Test grau. Hierbei handelt es sich um Back Edges oder Rückkanten im aufgespannten Baum. Eine mit B markierte Kante zeigt einen Zyklus an. Bei F Kanten werden beim Test schwarze Knoten gefunden, dessen Bearbeitungsintervall ins Intervall des aktuellen bearbeiteten Knotens passt. Es handelt sich hierbei um Forward Edges bzw. Vorwärtskanten in dem aufgespannten Baum. Bei C Kanten haben wir schwarze Zielknoten v, dessen Intervalle nicht in das aktuelle Intervall passen (d[u]>f[v]). Hierbei handelt es sich um Cross Edges, eine Kante die zwei aufgespannte Bäume verbindet.
Beispiel
BearbeitenDie Notation an den Knoten ist dabei durch <Beginn der Bearbeitung d> / <Ende der Bearbeitung f> gegeben.
Analyse
BearbeitenTheorem der Terminierung
BearbeitenDie Tiefensuche terminiert nach endlicher Zeit.
Theorem der Korrektheit
BearbeitenEs werden alle Knoten von G genau einmal besucht.
Theorem der Laufzeit
BearbeitenIst sowohl die Laufzeit von getChidlren linear in der Anzahl der Kinder als auch getNodes linear in der Anzahl der Knoten, so hat die Tiefensuche eine Laufzeit von O(|V|+|E|).
Anwendung
BearbeitenDer Tiefendurchlauf wird beispielsweise bei dem Test auf Zyklenfreiheit verwendet. Damit ein Graph zyklenfrei ist, darf kein Kreis K in dem Graph G vorhanden sein. Deshalb basiert dieser Test auf dem Erkennen von Back Edges. Er ist effizienter als beispielsweise die Konstruktion einer transitiven Hülle. Die Tiefensuche wird aber auch beim topologischen Sortieren verwendet. Topologisch bedeutet sortieren nach Nachbarschaft, nicht nach totaler Ordnung.
Topologisches Sortieren
BearbeitenAuf dieser Seite wird das topologische Sortieren behandelt. Wir fragen uns, wie Knoten unter Berücksichtigung von Abhängigkeiten aufgezählt werden können bei gegebenem azyklischem gerichteten Graph. Zur Anwendung kommt diese Sortierung bei Scheduling bei kausalen und zeitlichen Abhängigkeiten, zum Beispiel bei der Netzplantechnik. Mathematisch liegt hier eine Konstruktion einer totalen Ordnung aus einer Halbordnung vor.
Beispiel
BearbeitenDie sorgfältige Mutter legt ihrem Kind morgens die Kleidungsstücke so auf einen Stapel, dass das Kind nur die Kleidungsstücke vom Stapel nehmen und anziehen muss und dann richtig gekleidet ist. Hierfür legt sie die Reihenfolgebedingungen fest:
Unterhose vor Hose
Hose vor Gürtel
Unterhemd vor Gürtel
Gürtel vor Pulli
Unterhemd vor Rolli
Rolli vor Pulli
Socken vor Schuhen
Hose vor Schuhen
Uhr: egal
DFS erstellt die topologische Ordnung on the fly. Das Sortieren nach f-Wert (invers) ergibt eine korrekte Reihenfolge. Statt der expliziten Sortierung nach f werden beim Setzen des f-Wertes die Knoten vorne in eine verkettete Liste eingehängt.

18 Socken
16 Unterhose
15 Hose
14 Schuhe
10 Uhr
8 Unterhemd
7 Gürtel
5 Rolli
4 Pulli
Alternativer Durchlauf:
Berechnung kürzester Wege
BearbeitenAuf dieser Seite wird die Berechnung der kürzesten Wege behandelt.
Gegeben ist ein (Di-)Graph mit einer Gewichtsfunktion: . Der Pfad durch G ist eine Liste von aneinanderstoßenden Kanten . Das Gewicht oder die Länge eines Pfades ist die Aufsummierung der einzelnen Kantengewichte. . Die Distanz zweier Punkte d(u,v) ist das Gewicht des kürzesten Pfades von u nach v.
Es existieren verschiedene kürzeste Wege Probleme.
SPSP: Single pari shortest path
- Eingabe: Graph G, Startknoten s, Endknoten t
- Ausgabe: Distanz d(s,t)
SSSP: Single source shortest paths
- Eingabe: Graph G, Startknoten s
- Ausgabe: Distanzen d(s,v) für alle Knoten v
APSP: All-pairs shortest paths
- Eingabe: Graph G
- Ausgabe: Distanzen d(v,w) für alle Knoten v,w
Auf den nächsten Seiten lernen wir zwei Algorithmen zum Berechnen des kürzesten Weges kennen.
Dijkstra Algorithmus
BearbeitenAuf dieser Seite wird der Dijkstra Algorithmus behandelt. Der Dijkstra Algorithmus wird zur Berechnung des kürzesten Weges benutzt (SSSP). Der Algorithmus stammt von 1959. Es erfolgt eine iterative Erweiterung einer Menge von günstig erreichbaren Knoten. Der Greedy Algorithmus hat eine ähnliche Breitensuche ist aber nur für nichtnegative Gewichte. Er berechnet iterativ verfeinert die Distanzwerte d(v,w) und es gibt eine Prioritätswarteschlange zum Herauslesen des jeweils minimalen Elements.
Priority Queues
BearbeitenEine Priority‐Queue P ist eine dynamische Datenstruktur, die (mindestens) die folgenden Operationen unterstützt:
- P.add(Element): Element hinzufügen
- P.poll(): Minimalste Element zurückgeben
- P.contains(Element): Enthält P das Element?
Die Ordnung zur Sortierung muss dabei vorab definiert sein.
Ein Heap kann beispielsweise zur Implementierung einer Priority‐Queue benutzt werden (add‐Operation ist dann O(log n), poll‐Operation O(log n), und contains‐Operation ist O(n)). Benutzt man zusätzlich zum Heap noch einen binären Suchbaum auf denselben Element so ist auch contains in O(log n) realisierbar.
Priority Queue in Java
Bearbeitenclass DijkstraComparator implements Comparator<Integer>{
Map<Integer,Integer> d = new HashMap<Integer,Integer>();
public DijComparator(Map<Integer,Integer> d){
this.d = d;
}
public int compare(Integer o1, Integer o2) {
return d.get(o1).compareTo(d.get(o2));
}
}
Ist d eine Map “Knoten”‐>”Aktueller Distanzwert von s aus”, so ist PriorityQueue<Integer> queue = new PriorityQueue<Integer>(g.getNumberOfNodes(),new DijkstraComparator(d)); eine Priority‐Queue, die bei iterativen Aufruf queue.poll() immer das Element mit dem minimalsten d‐Wert zurückliefert.
Idee
Bearbeiten- Initialisiere alle Distanzwerte von s zu v mit ∞ (und von s zu s mit 0)
- Initialisiere eine Priority‐Queue Q mit allen v
- Extrahiere das minimale Element aus Q
- Aktualisiere alle Distanzwerte der Nachfolger von in Q:
- Ist es günstiger über zu einem Knoten w zu kommen?
- Falls ja setzte d(s,w)=d(s,)+y(,w)
- 5. Wiederhole bei 3 solange Q noch Elemente hat
Algorithmus in Java
BearbeitenMap<Integer,Integer> dijkstra(Graph g, int s){
Map<Integer,Integer> d = new HashMap<Integer, Integer>();
PriorityQueue<Integer> queue = //Initialisiere Priority-Queue entsprechend
for(Integer n: g){
if(!n.equals(s)){
d.put(n, Integer.MAX_VALUE);
queue.add(n);
}
}
d.put(s, 0);
queue.add(s);
while(!queue.isEmpty()){
Integer u = queue.poll();
for(Integer v: g.getChildren(u)){
if(queue.contains(v)){
if(d.get(u) + g.getWeight(u,v) < d.get(v){
d.put(v, d.get(u) + g.getWeight(u,v));
}
}
}
}
return d;
}
Algorithmus
Bearbeitenalgorithm Dijkstra (G,s)
- Eingabe: Graph G mit Startknoten s
- for each Knoten u V[G] -s do // Initialisierung
- D[u] :=
- od;
- D[s]:= O; PriorityQueue Q := V;
- while not isEmpty (Q) do
- U := extractMinimal (Q);
- for each v ZielknotenAusgehenderKanten (u) Q do
- if D[u] + ((u,v)) < D[v] then // Entfernung über u nach v kleiner als aktuelle Entfernung D[v]
- D[v] := D[u] + ((u,v));
- adjustiere Q an neuen Wert D[v]
- fi
- if D[u] + ((u,v)) < D[v] then // Entfernung über u nach v kleiner als aktuelle Entfernung D[v]
- od
- od
- for each Knoten u V[G] -s do // Initialisierung
Initialisierung
Bearbeiten

Der Iterationsstart ist korrekt für die Tiefe 0. Wir nehmen an, dass der vorherige Iterationsschritt korrekt war ( Induktionsbeweis). Der Ein Iterationsschritt ist jeweils die günstigste Verbindung zu einem noch nicht bearbeiteten Knoten hinzunehmen. Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt. Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzu genommenen Kanten nicht sinken können.
Analyse
BearbeitenTerminierungstheorem
BearbeitenDer Algorithmus von Dijkstra terminiert für eine endliche Eingabe nach endlicher Zeit.
Beweis
BearbeitenIn jedem Schritt der while‐Schleife wird ein Element aus queue entfernt und die Schleife endet sobald queue leer ist. Jeder Knoten hat nur endliche viele Kinder, deswegen ist auch die Laufzeit der inneren for‐Schleife endlich.
Korrektheitstheorem
BearbeitenSind alle Kantengewichte nicht‐negativ, so enthält d am Ende die Distanzwerte von s zu allen anderen Knoten.
Beweis
BearbeitenBeachte, dass sobald ein Knoten v aus queue entfernt wird, der Wert für v in d nicht mehr geändert wird.
Zeige nun, dass gilt: Wird v aus queue entfernt, so enthält d den Distanzwert von s nach v. Zeige dies durch Induktion nach i=„Anzahl bisher aus queue entfernter Knoten“:
- i=0: Am Anfang hat queue nur für s einen endlichen Wert gespeichert, alle anderen Werte sind ∞. Der Knoten s wird auch stets zuerst entfernt und der Distanzwert ist 0. Dies ist auch korrekt, da s zu sich selbst Distanz 0 hat und alle anderen Knoten keine geringere Distanz von s aus haben können (da alle Kanten nicht‐negative Gewichte haben).
- i → i+1: Sei v der (i+1)te Knoten, der aus queue entfernt wird.
- Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt.
- Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzugenommenen Kanten nicht sinken können.
Laufzeittheorem
BearbeitenSei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand von Dijkstras Algorithmus für einen beliebigen Knoten s in G ist O((|E| + |V|) log |V|).
Beweis
BearbeitenBeachte: Wird für die Priority‐Queue beispielsweise ein Heap verwendet, so hat die Operation poll() einen Aufwand von O(log k) (mit k=„Anzahl Elemente in Queue“). Sei |V|=n und |E|=m. Insgesamt: O(n log n) + O(n) + n* O(log n) + m *O(log n) = O((m + n) log n) Durch Benutzung sog. Fibonacci‐Heaps (anstatt normaler Heaps) kann die Laufzeit von O((m + n) log n) verbessert werden zu O(m + n log n)
Nachteile
BearbeitenDer kürzeste Weg wird immer gefunden, aber es werden viele unnötige und sinnlose Wege gegangen. Bei negativen Kanten resultieren auch falsche Ergebnisse.
Bellmann-Ford
BearbeitenAuf dieser Seite wird der Bellmann-Ford Algorithmus behandelt. Bei Dijkstra dürfen nur nichtnegative Gewichte benutzt werden. Doch gibt es auch eine Variante mit negativen Gewichten? Das würde nur bei gerichteten Graphen Sinn machen. Das Problem sind Zyklen mit negativem Gesamtgewicht. Ein Beispiel für Gewinn statt Kosten ist beispielsweise ein Verbindungsnetz mit Bonus Gewinnen für bestimmte Verbindungen um Auslastungen zu erhöhen. Dies ist bei Flügen mit Zwischenstopps der Fall, die oft billiger sind. Dieser Algorithmus löst ebenfalls das SSSP Problem.
Prinzip
BearbeitenDer Algorithmus erfolgt in mehreren Durchläufen. Es wird zunächst die bisher beste mögliche Verbindung bestimmtl, die die um eine Kante länger ist. Der i-te Durchlauf berechnet korrekt alle Pfade vom Startknoten der Länge i. Der längste Pfad ohne Zyklus hat eine Länge kleiner als |V|-1, somit hat man spätestens nach |V|-1 Durchläufen ein stabiles Ergebnis. Sollte das Ergebnis nach |V|-1 Durchläufen nicht stabil sein, so ist ein negativ bewerteter Zyklus enthalten. Hierbei wird das Prinzip der dynamischen Programmierung verwendet.
Algorithmus
Bearbeitenalgorithm BF(G, s)
Eingabe: ein Graph G mit Startknoten s
D[s] = 0
D[t] = ∞ for all other t
for i := 1 to |V|-1 do
for each (u,v)∈ E do
if D[u]+γ((u,v)) < D[v] then
D[v] := D[u] + γ((u,v))
fi
od
od
Beispiel
BearbeitenBei der Initialisierung wird der Startknoten auf den Wert 0 gesetzt und alle weiteren Knoten erhalten den Wert ∞.
Beim ersten Schleifendurchlauf bekommt x den Wert 5 und u den Wert 10 zugewiesen.
Im zweiten Schleifendurchlauf werden alle weiteren Verbindungen aktualisiert, sowohl von u als auch von x. Dabei ändern sich die Werte von v, y und auch u. Die Änderung an u wird aber erst im nächsten Schritt an v propagiert.
Im dritten, i=3, Schleifendurchlauf verändern sich diesmal nur noch die Werte der Knoten v und y. Der neue Wert aus y berechnet sich durch den vorherigen Wert aus v=11 und der negativ gewichteten Kante -5. Hier wird also die negativ gewichtete Kante (v,y) zur Berechnung von D[y] genutzt.
Im vierten, i=4, Schleifendurchlauf wird nochmals die negativ gewichtete Kante (v,y) zur Berechnung von D[y] genutzt. Das Greedy-Verfahren, das jeden Knoten nur einmal besucht, hätte für y den in jedem Schritt lokal optimalen Pfas gewählt und nicht das beste Ergebnis geliefert.
Analyse
BearbeitenTerminierungstheorem
BearbeitenDer Algorithmus BF(G,s) terminiert für eine endliche Eingabe G in endlicher Zeit.
Beweis
BearbeitenAlle Schleifen sind endlich.
Korrektheitstheorem
BearbeitenIst G ein Graph, der keinen Zyklus mit negativem Gewicht hat, so enthält D nach Aufruf BF(G,s) die Distanzwerte von s zu allen Knoten.
Beweis
BearbeitenWir zeigen, dass die folgenden Aussagen Schleifeninvariante der for‐ Schleife (Schleifenvariable i) sind:
- Ist D[v] < ∞, so ist D[v] der Wert eines Pfades von s nach v
- Ist D[v] < ∞, so ist D[v] der kleinste Wert eines Pfades von s nach v mit maximal i Kanten
- D[v] < ∞ gdw. es einen Pfad von s nach v mit gleich oder weniger als i Kanten gibt
Da G keine Zyklen mit negativem Gewicht hat, ist die Länge des längsten kürzesten Pfades maximal |Anzahl Knoten|‐1 (jeder Knoten wird auf diesem Pfad einmal besucht). Also gilt nach dem letzten Schleifendurchlauf nach 2 und 3. die Aussage des Theorems. Wir zeigen diese Aussagen durch Induktion nach i(=#Schleifendurchläufe).
- Bei i=0 gilt vor dem ersten Schleifendurchlauf nur D[s]=0 < ∞. Daraus folgt direkt 1., 2., 3.
- Bei i -> i+1 beweisen wir zunächst Aussage 3.
- War D[v] schon vorher endlich, so gilt die Aussage nach IV.
- Ist D[v] in diesem Schritt auf einen endlichen Wert gesetzt worden, so gab es ein u, so dass D[u] vorher schon endlich war und D[v]=D[u]+γ(u,v). Nach IV gibt es einen Pfad von s nach u der Länge i. Damit gibt es einen Pfad der Länge i+1 von s nach v.
- Umgekehrt wird bei Existenz eines Pfades der Länge i+1 dieser auch gefunden und D[v] auf einen endlichen Wert gesetzt.
- Die Aussage 1 wird dadurch bewiesen, dass nach IV der Wert eines Pfades von s nach u D[u] ist. Wird D[v]=D[u]+γ(u,v) gesetzt so ist somit D[v] der Wert des Pfades von s nach v über u.
- Die Aussage 2 wird dadurch bewiesen, dass nach IV der kleinste Wert eines Pfades von s nach v mit maximal i Kanten D[v] ist. Mache folgende Fallunterscheidung:
- 1.Fall: Es existiere ein Pfad P1 von s nach v mit i+1 Kanten, der minimalen Wert unter allen Pfaden von s nach v mit gleich oder weniger als i+1 Kanten hat. Betrachte den vorletzten Knoten u auf diesem Pfad und den Teilpfad P2 von P1 von s nach u. Dieser Teilpfad hat minimalen Wert unter allen Pfaden der maximalen Länge i von s nach u (ansonsten wäre P1 kein Pfad mit minimalem Wert). Nach IV ist D[u] genau dieser Wert und D[u]+γ(u,v) der Wert von P1, der dann im i+1ten Durchgang aktualisiert wird.
- 2.Fall: Es existiere kein Pfad von s nach v mit i+1 Kanten, der minimalen Wert unter allen Pfaden von s nach v mit gleich oder weniger als i+1 Kanten hat.
- 1. Unterfall: Es existiert kein Pfad von s nach v mit maximal i+1 Kanten. Dann bleibt nach 3. D[v]=∞.
- 2. Unterfall: Es existiert ein Pfad von s nach v mit k<i+1 Kanten, der minimalen Wert unter allen Pfaden von s nach v mit gleich oder weniger als i+1 Kanten hat. Dann ist nach IV D[v] genau dieser Wert und wird im i+1ten Durchgang auch nicht aktualisiert.
Graph mit negativ gewichtetem Zyklus
Bearbeiten
Betrachten wir die Situation nach |V|-1 Iterationen. Eine Kante könnte noch verbessert werden genau dann wenn der Graph einen Zyklus negativer Länge enthält. Der Zyklus s,x,u,v,y,s hat die Kosten 5+3+1-5-7=-3. Jeder Durchlauf durch den Zyklus erzeugt also einen Gewinn. Es gibt hier keinen günstigen Pfad endlicher Länge!
Laufzeittheorem
BearbeitenSei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand vom Algorithmus von Bellmann‐Ford für einen beliebigen Knoten s in G ist O(|V||E|).
Beweis
BearbeitenEinfache Schleifenanalyse.
Floyd-Warshall
BearbeitenAuf dieser Seite wird der Floyd-Warshall Algorithmus behandelt. Der Dijkstras Algorithmus und Bellman-Ford berechnen zu einem gegebenen Startknoten die kürzesten Wege zu allen anderen Knoten (Single Source Shortest Paths – SSSP. Aber wie kann man die kürzesten Wege zwischen zwei Knoten v und w berechnen? Man könnte die bereits kennengelernten Algorithmen für jeden einzelnen Startknoten neu aufrufen, doch das geht auch geschickter. Hier kommt der Floyd-Warshall Algorithmus ins Spiel, welcher das All Pairs Shortest Path Problem löst. Zwar nicht unbedingt effizienter, aber eleganter. Dies geschieht nach dem Prinzip der dynamischen Programmierung.
Problemdefinition
BearbeitenGegeben ist ein Graph G=(V,E). Wir möchten für jedes Paar den Wert D(v,w) eines kürzesten Pfades finden. Wir nehmen an, dass es keine negativen Kreise gibt.

| D | s | u | v | x | y |
| s | 0 | 8 | 9 | 5 | 4 |
| u | 3 | 0 | 1 | -2 | -4 |
| v | 2 | 10 | 0 | 7 | -5 |
| x | 6 | 3 | 4 | 0 | -1 |
| y | 7 | 15 | 6 | 12 | 0 |
Idee
BearbeitenDie Grundidee des Floyd-Warshall Algorithmus ist, dass wenn ein kürzester Weg von v nach w über k geht, dann gilt:
- ist ein kürzester Weg von v nach k
- ist ein kürzester Weg von k nach w
Im obigen Beispiel gilt folgendes:
Die Umkehrung gilt jedoch nicht. Ist ein kürzester Weg von v nach k und ist ein kürzester Weg von k nach w dann gilt nicht notwendigerweise, dass ein kürzester Weg von v nach w ist!
Im obigen Beispiel bedeutet dies:
- ist nicht der kürzeste Weg!
Jedoch gilt, wenn bekannt ist, dass ein kürzester Weg zwischen v und w nur Knoten aus enthält, so gilt entweder der kürzeste Weg zwischen v und w benutzt nur Knoten aus oder der kürzeste Weg zwischen v und w ist Konkatenation aus dem kürzesten Weg zwischen v und k und dem kürzesten Weg zwischen k und w und beide Wege enthalten nur Knoten aus .
Algorithmus
Bearbeitenalgorithm FW(G)
Eingabe: ein Graph G
for each v,v‘∈V
D[v,v‘] = γ((v,v‘)) (or ∞)
for each k ∈ V do
for each i ∈ V do
for each j ∈ V do
if D[i,k]+D[k,j] < D[i,j] then
D[i,j] := D[i,k]+D[k,j]
fi
od
od
od
Beispiel
BearbeitenInitialisiere D mit den Kantengewichten. Nicht vorhandene Kanten haben das Gewicht . Die Kantengewichte zum Knoten selber sind 0. Im folgenden betrachten wir nur Schleifendurchgänge mit

| D | s | u | v | x | y |
| s | 0 | 10 | 5 | ||
| u | 0 | 1 | -2 | ||
| v | 0 | -5 | |||
| x | 3 | 0 | 2 | ||
| y | 7 | 6 | 0 |










| D | s | u | v | x | y |
| s | 0 | 10 | 5 | ||
| u | 0 | 1 | -2 | ||
| v | 0 | -5 | |||
| x | 3 | 0 | 2 | ||
| y | 7 | 17 | 6 | 0 |


| D | s | u | v | x | y |
| s | 0 | 10 | 5 | ||
| u | 0 | 1 | -2 | ||
| v | 0 | -5 | |||
| x | 3 | 0 | 2 | ||
| y | 7 | 17 | 6 | 12 | 0 |

Führt man den Algorithmus weiter durch, kommt man zu folgendem Endergebnis:
| D | s | u | v | x | y |
| s | 0 | 8 | 9 | 5 | 4 |
| u | 3 | 0 | 1 | -2 | -4 |
| v | 2 | 10 | 0 | 7 | -5 |
| x | 6 | 3 | 4 | 0 | -1 |
| y | 7 | 15 | 6 | 12 | 0 |
Analyse
BearbeitenTerminierungstheorem
BearbeitenDer Algorithmus FW(G) terminiert für eine endliche Eingabe G in endlicher Zeit.
Beweis
BearbeitenAlle Schleifen sind endlich.
Korrektheitstheorem
BearbeitenIst G ein Graph, der keinen Zyklus mit negativem Gewicht hat, so enthält D nach Aufruf FW(G) die Distanzwerte von allen Knoten zu allen anderen Knoten.
Beweis
BearbeitenBetrachte dazu folgende Schleifeninvariante, die äußerste for-Schleife mit der Laufvariablen k): Nach der k-ten Schleifeniteration gilt, dass D[v,w], für alle v,w, der Wert eines kürzesten Pfades ist, der nur Knoten 1,...,k benutzt. Wenn der Algorithmus endet, gilt damit die Aussage des Theorems. Dies zeigen wir durch Induktion.
- k=0 (bei der Initialisierung): Nach der Initialisierung gilt D[v,w]= ∞ gdw. es keine Kante von v nach w gibt. Das bedeutet, dass jeder Pfad zwischen v und w mindestens einen anderen Knoten enthalten haben muss. Ist D[v,w] endlich, so ist dies genau der Wert der Kante. Dann gibt es also einen Pfad, der keine weiteren Knoten beinhaltet.
- k -> k+1: Nach der Induktionsannahme ist D[v,w] der Wert eines kürzestens Pfades, der nur Knoten aus 1,...,k enthält. Im k+1-Schleifendurchgang wird überprüft, ob es einen kürzeren Weg über k+1 gibt und ggfs. aktualisiert. Es wird also genau folgende Gleichung ausgenutzt:
Anschließend ist also D[v,w] der Wert eines kürzestens Pfades, der nur Knoten 1,...,k+1 benutzt.
Ein anderer Ansatz ist dies per Induktion nach der kürzesten Länge eines kürzesten Weges für jedes Knotenpaar (v,w) zu zeigen. Anmerkung: zwischen v und w können mehrere Wege mit minimalem Gewicht existieren, diese können auch unterschiedliche Länge haben. Angenommen zwischen v und w existiert ein kürzester Weg der Länge 1, dann ist der Wert dieses Weges gleich dem Wert der Kante (die existieren muss. Dieser wird in der Initialisierungsphase gesetzt und später nicht mehr geändert. Angenommen zwischen v und w gibt es einen kürzesten Pfad (=minimales Gewicht) der Länge l≥ 2 , dann gibt es einen Knoten k auf diesem Pfad, so dass zum einen der Teilpfad von v nach k ein kürzester Weg von v nach k ist und zum anderen, dass der Teilpfad von k nach w ein kürzester Weg von k nach w ist. Somit haben beide Pfade haben Länge < l, d.h. die Werte D[v,k] und D[k,w] müssen schon korrekt berechnet sein (die Induktionsvoraussetzung greift). Da alle potentiellen “Mi5elknoten” überprüft werden, wird ein geeignetes k gefunden und der Wert D[v,w] aktualisiert.
Laufzeittheorem
BearbeitenSei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand vom Algorithmus von Floyd‐Warshall auf G ist ).
Beweis
BearbeitenEinfache Schleifenanalyse.
Flussproblem
BearbeitenAuf dieser Seite wird das Flussproblem behandelt. Die Bestimmung des maximalen Flusses muss in vielen logischen Aufgaben angewandt werden. Beispielsweise bei Verteilungsnetzen mit Kapazitäten wie Wasserrohren, Förderbändern oder Paketvermittlungen mit Rechnernetzen. Die Quellen liefert beliebig viele Objekte pro Zeiteinheit und die Senke verbraucht diese. Jede Verbindung hat eine maximale Kapazität c und einen aktuellen Fluss f. Wie hoch ist nun die Übertragungskapazität?
Definition Fluss
BearbeitenEin Fluss f von nach ist eine Funktion . Für diese Funktion gelten folgende zwei Bedingungen:
- Die Kapazitäten werden eingehalten:
- Was in einen Knoten hereinfließt, muss wieder herausfließen, mit Ausnahme von q und z: , wobei der Vorgänger von v ist und der Nachfolger von v ist.
Einschränkungen der Kapazität der Kanten werden eingehalten, auch bei negativem Fluss:
Außerdem ist der Fluss konsistent. Bei in beiden Richtungen nutzbaren Verbindungen wird als Nettoeffekt nur in eine Richtung gesendet und der entstehende negative Fluss nimmt den korrekten Wert an:
Der Fluss wird für jeden Knoten mit Ausnahme der Quelle q und des Ziels z bewahrt:
Der Wert eines Flusses beträgt:
Gesucht wird der maximale Fluss:
f ist korrekter Fluss von q nach z}
Beispiel
BearbeitenDefiniere durch
.
Daraus folgt, dass der Wert des Flusses 6 ist: .

Definiere durch
.
Daraus folgt, dass kein Fluss ist.
Definiere durch
.
Daraus folgt, dass der Wert des Flusses 14 ist: . Damit ist der Fluss maximal.

Ford-Fulkerson
BearbeitenAuf dieser Seite wird der Ford Fulkerson Algorithmus zur Berechnung des maximalen Flusses behandelt.
Berechnung des maximalen Flusses
BearbeitenDer Ford-Fulkerson Algorithmus ist ein effizienter Algorithmus zur Bestimmung eines maximalen Flusses von q nach z. Dabei wird der Greedy Algorithmus mit Zufallsauswahlen gemischt. Hier wird das Prinzip "Füge so lange verfügbare Pfade zum Gesamtfluss hinzu wie möglich" verfolgt. Zuerst soll ein nutzbarere Pfad durch Tiefensuche gefunden werden. Für die Kanten werden dann drei Werte notiert. Zum einen der aktuellen Fluss entlang der Kante. Im initialisierten Graphen ist dieser Wert überall 0. Zudem wird die vorgegebene Kapazität c notiert und die abgeleitete noch verfügbare Restkapazität von c-f.
Algorithmus
Bearbeiteninitialisiere Graph mit leerem Fluss;
do
wähle nutzbaren Pfad aus;
füge Fluss des Pfades zum Gesamtfluss hinzu;
while noch nutzbarer Pfad verfügbar
Ein nutzbarere Pfad ist ein zyklenfreier Pfad von der Quelle q zum Ziel z, der an allen Kanten eine verfügbare Kapazität hat. Ein nutzbarer Fluss ist das Minimum der verfügbaren Kapazitäten der einzelnen Kanten.
Der nachfolgende Pseudocode realisiert das Problem mit zusätzlichen Rückkanten.
für jede Kante(u,v) füge Kante (v,u) mit Kapazität 0 ein;
initialisiere Graph mit leerem Fluss;
do
wähle nutzbaren Pfad aus;
füge Fluss des Pfades zum Gesamtfluss hinzu;
while noch nutzbarer Pfad verfügbar
Beispiele
Bearbeiten
Wir haben einen Graph mit Kapazitäten gegeben

Es wird mit dem Fluss 0 initialisiert. Notation: <aktueller Fluss f> / <Kapazität c> / <verfügbare Kapazität c-f>

Die Auswahl der nutzbaren Pfade geschieht zufällig oder durch geeignete Heuristik. Es gibt auch kürzere Pfade mit höheren Kapazitäten. Die Rückkanten werden mit der Kapazität 0 eingefügt. Die Auswahl eines Pfades geschieht durch Der nutzbare Fluss beträgt 4.

Der Fluss wird aktualisiert. Die Auswahl des Pfades ist nun : . Der nutzbare Fluss beträgt 5.

Der Fluss wird aktualisiert. Die Auswahl des Pfades ist nun : . Der nutzbare Fluss beträgt 3.
Der Fluss wird aktualisiert. Die Auswahl des Pfades ist nun : . Der nutzbare Fluss beträgt 2.

An dieser Stelle sind keine Kapazitäten mehr über und die Berechnung wir beendet. Der maximale Fluss beträgt 14.
Der Algorithmus kann dabei auf verschiedene Ergebnisse kommen, jedoch ist der maximale Fluss immer gleich. Eine weitere Lösung ist folgende:
Zunächst wird der Pfad mit dem nutzbaren Fluss 5 ausgewählt.

Anschließend wird der Fluss aktualisiert. Im nächsten Schritt wird dann der Pfad gewählt. Ebenfalls ist hier wieder ein nutzbarer Fluss von 5.

Nach der zweiten Aktualisierung ist nur noch ein Pfad vom Start zum Ziel möglich. Also wird der Pfad ausgewählt. Dieser Fluss enthält allerdings nur noch einen nutzbaren Fluss von 4.

Nach dem Aktualisieren des Flusses ist es nicht mehr möglich einen Pfad vom Start zum Ziel zu finden. Damit ist die Berechnung beendet. Wie zuvor berechnet ist der maximale Fluss 14.

Problem: Ungünstige Pfadwahl
BearbeitenDie bisher betrachtete Version des Algorithmus ist nicht immer optimal.
Wählen der Pfad ausgewählt, besitzt dieser Pfad einen nutzbaren Fluss von 5.
Nun wird der Fluss aktualisiert. Daraus folgt, dass keine weitere Pfadwahl mehr möglich ist. Dabei wäre die optimale Lösung über die Pfade und .
Das Problem ist, dass der Fluss nicht zurückgenommen werden kann. Die Lösung dazu ist, dass man entgegengesetzte Flussrichtung durch Rückkanten erlaubt. Auch hier wird wieder der ungünstige Pfad mit einem nutzbaren Fluss von 5 im ersten Schritt ausgewählt.
Anschließend wird der Fluss aktualisiert. Dabei wird der Pfad mit dem nutzbaren Fluss von 5 ausgewählt.
Beim erneuten aktualisieren des Flusses, stellt sich heraus, dass keine weiteren Pfade möglich sind. Damit ist die Berechnung, bei einem maximalen Fluss von 10, beendet.
Analyse
BearbeitenTerminierungstheorem
BearbeitenSind alle Kapazitäten in G nicht-negativ und rational, dann terminiert der Algorithmus von Ford‐Fulkerson nach endlicher Zeit.
Laufzeittheorem
BearbeitenIst X der Wert eines maximales Flusses in G=(V,E) und sind alle Kapazitäten in G nicht-negativ und ganzzahlig, so hat der Algorithmus von Ford‐Fulkerson eine Laufzeit von O(|E|X).
Korrektheitstheorem
BearbeitenSind alle Kapazitäten in G nicht‐negativ und rational, dann berechnet der Algorithmus von Ford‐Fulkerson den Wert eines maximalen Flusses.
Anmerkung
BearbeitenDie Wahl des Pfades beeinflusst die Anzahl benötigter Iteratoren. Bei dem Verfahren von Edmons und Karp muss die Anzahl der Pfade die in einem Graphen G = (V,E) bis zum Finden des maximalen Flusses verfolgt werden, kleiner sein als |V||E|, wenn jeweils der kürzeste Pfad von Quelle q zu Ziel z gewählt wird. Daher kann die Auswahl des nächsten kürzesten Pfades basierend auf einer Variante der Breitensuche erfolgen. Dadurch wird die Laufzeit auf verbessert.
Spannbäume
BearbeitenAuf dieser Seite werden Spannbäume und in diesem Zusammenhang der Algorithmus von Prim behandelt.
Beispiel Kommunikationsnetz
BearbeitenZwischen n Knotenpunkten soll ein möglichst billiges Kommunikationsnetz geschaltet werden, so dass jeder Knotenpunkt mit jedem anderen verbunden ist, ggf. auf einem Umweg über andere Knotenpunkte. Bekannt sind die Kosten für die direkte Verbindung zwischen und . Alle Kosten seien verschieden und größer Null. Die Modellierung geschieht somit als gewichteter, ungerichteter und vollständiger Graph mit einer Gewichtungsfunktion c.

etc; abgekürzt etc
Problemstellung: Finde minimal aufspannenden Baum
BearbeitenEinige Definitionen für ungerichtete Graphen:
Ein Graph G=(V,E) heißt zusammenhängend, wenn für alle v,w∈V ein Pfad von v nach w in G existiert.
Ein Graph G=(V,E) enthält einen Zyklus, wenn es unterschiedliche Knoten gibt, so dass . Ein Graph G=(V,E) heißt Baum, wenn er zusammenhängend ist und keinen Zyklus enthält.
Ein Graph G’=(V’,E’) heißt Teilgraph von G=(V,E), wenn und .
Ein Graph G’=(V’,E’) heißt induzierter Teilgraph von G=(V,E) bzgl. , wenn
Ein Graph G‘=(V‘,E‘) heißt Spannbaum von G=(V,E), wenn V'=V und G' ein Teilgraph von G und ein Baum ist.
Das Gewicht einen Graphen G=(V,E) ist .
Ein Graph G'=(V',E') ist ein minimaler Spannbaum von G=(V,E), wenn G' ein Spannbaum von G ist und G' unter allen Spannbäumen von G das minimalste Gewicht hat.
Algorithmus von Prim
BearbeitenDer Algorithmus wird schrittweise verfeinert und der Aufbau eines aufgespannten Baumes erfolgt durch das Hinzufügen von Kanten. Das Greedy Muster, also jeweils die Wahl der kostengünstigsten Kante als Erweiterung, wird hier benutzt.
Aufspannender minimaler Baum
Bearbeiten//Teilbaum B besteht anfangs aus einem beliebigen Knoten
while [ B noch nicht GV aufspannt ]
do [ suche kostengünstige von B ausgehende Kante ];
[ füge diese Kante zu B hinzu ];
od
Eine Verfeinerung der Suche nach der kostengünstigsten Kante ist notwendig!
Suche nach kostengünstigster Kante
BearbeitenDie intuitive Vorgehensweise erfordert jeweils |W|(|V|-|W|) Vergleiche für ein gegebenes W. Das ganze |V| mal, also eine Gesamtlaufzeit von . Man kann die Suche auf die Teilmengen beschränken, so dass F immer die günstigste aus b ausgehende Kante enthält, wesentlich weniger Kanten hat als |W|(|V|-|W|) und im Verlauf des Algorithmus einfach anpassbar ist.
Wahl von F
BearbeitenAlternativen:
a) F enthält für jeden Knoten v in B die günstigste von v aus B herausführende Kante
b) F enthält für jeden Knoten v außerhalb B die günstigste von v in B hineinführende Kante
Bewertung:
a) Mehrere Kanten können zum gleichen Knoten herausführen – redundant und änderungsaufwändig (bei Wahl dieses Knotens darf er nicht mehr verwendet werden und alle Verbindungen zu diesem Knoten müssen gelöscht werden)
b) Daher: Wahl von b)
Erste Verfeinerung
Bearbeiten// Teilbaum B
[ B:= ({ beliebiger Knoten v }, {}) ]
// Menge der Kandidatenkanten F
[ F:= alle nach v führenden Kanten ]
// alle Knoten betrachten
for i := 1 to |V|-1
do [ suche günstigste Kante f=(u,w) in F ];
[ Füge f zu B hinzu (natürlich auch w) ];
[ Aktualisiere F ];
od
F muss nach jedem Durchlauf angepasst werden. Wenn f aus F entfernt wird erkennt man, dass der Teilgraph B tatsächlich ein Baum ist. Nun haben wir den neu verbundenen Knoten w. Jeder noch nicht verbundene Knoten x hat nun eine günstigste Verbindung entweder wie zuvor, oder aber mit dem neu hinzugefügten Knoten w!
Zweite Verfeinerung
Bearbeiten// Teilbaum B
[ B:= ({ beliebiger Knoten v },{}) ]
// Menge der Kandidatenkanten F
[ F:= alle nach v führenden Kanten ]
for i := 1 to |V|-1
do
// Sei v∈B, w∈B
[ suche günstigste Kante f=(v,w) in F ];
[ Füge f zu B hinzu ];
// Aktualisiere F
[ Entferne f aus F ];
// x in B, w neuerdings in B, y noch nicht in B
for [ alle Kanten e=(x,y)∈F]
do
if [ c((w,y))<c(e)] then [ Ersetze e durch (w,y) ] fi
od
od
Kommunikationsnetz
Bearbeiten
i:
ist am günstigsten
….
Analyse
BearbeitenTerminierungstheorem
BearbeitenDer Algorithmus von Prim terminiert nach endlicher Zeit.
Beweis
BearbeitenEinfache Schleifenanalyse
Laufzeittheorem
BearbeitenWird für die Implementierung von F ein Fibonacci‐Heap benutzt, so hat der Algorithmus von Prim eine Laufzeit von O(|E| + |V| log |V|).
Korrektheitstheorem
BearbeitenIst G ein verbundener ungerichteter gewichteter Graph, so berechnet der Algorithmus von Prim einen minimalen Spannbaum von G.
Beweis
BearbeitenWir betrachten eine einfache Version des Algorithmus.
while [ B noch nicht GV aufspannt ]
do [ suche kostengünstige von B ausgehende Kante ];
[ füge diese Kante zu B hinzu ];
od
Wir beobachten, dass B am Ende ein Spannbaum ist. Jetzt ist noch zu zeigen, dass B am Ende ein minimaler Spannbaum ist.
Sei B‘ ein minimaler Spannbaum von G und B≠B‘. Betrachte den Zeitpunkt in der Hauptschleife, an dem sich die Konstruktion von B von B‘ unterscheidet. Sei e die Kante, die dann zu B hinzugefügt wird. Sei die Menge der Knoten, die schon in B sind und \ Da B‘ ein minimaler Spannbaum ist, gibt es eine Kante e', die mit verbindet. Da im Algorithmus stets eine günstigste Kante gewählt wird, muss gelten g(e)≤g(e‘). Tauschen wir in B‘ die Kante e‘ durch e erhalten wir also einen minimalen Spannbaum, der nicht mehr kostet als B‘, es folgt g(e)=g(e‘). Induktiv folgt damit die Korrektheit.
Grundlagen
BearbeitenGrundlagen der Optimierung
BearbeitenAuf dieser Seite gibt es eine Einführung in das Thema Optimierung.
Die (Mathematische) Optimierung beschreibt eine Familie von Lösungsstrategien zur Maximierung/Minimierung einer Zielfunktion unter Nebenbedingungen. Viele der bisher untersuchten Probleme können als Optimierungsproblem modelliert werden. Zum Beispiel das Kürzeste Wege Problem: Minimiere die Länge eines Pfades unter der Nebenbedingung, dass der Pfad zwei gegebene Knoten verbindet. Oder das Rucksackproblem: Maximiere den Gesamtnutzen der Gegenstände unter der Nebenbedingung, dass die Kapazität des Rucksacks eingehalten wird. Oder das Flussprobleme: Maximiere den Fluss unter der Nebenbedingung, dass Kantenkapazitäten eingehalten werden.
Algorithmen wie Djikstra und Ford-Fulkerson sind domänenspezifische Algorithmen zur Lösung ihrer jeweiligen Optimierungsprobleme. Mathematische Optimierungsverfahren sind allgemeine Verfahren, die auf eine Vielzahl von Problemen anwendbar sind, dabei aber eventuell nicht immer so effizient wie speziellere Algorithmen sind.
Optimierung ist eine weites Feld, wir werden uns in dieser Vorlesung auf einen kleinen Ausschnitt konzentrieren:
- Grundlagen der Optimierung
- Kombinatorische Optimierung
- Lineare Optimierung
- Das Simplex‐Verfahren
Begriffe
BearbeitenEin allgemeines (reelles) Optimierungsproblem ist gegeben durch P: Minimiere f(x)unter der Nebenbedingung . f ist dabei die Zielfunktion. heißt zulässig für P, falls . X ist die zulässige Menge und heißt globales Minimum von P, falls . Äquivalent gilt P: Minimiere f(x) unter der Nebenbedingung und P': Maximiere -f(x) unter der Nebenbedingung .
Beispiel Gewinnmaximierung
BearbeitenEine Firma produziert zwei verschiedene Waren. Ware x1 erbringt einen Gewinn von einem Euro. Ware x2 erbringt einen Gewinn von 6 Euro.
Frage: Welches Verhältnis von x1 und x2 führt zum größten Gewinn?
Nebenbedingungen:
Die Firma kann täglich maximal 200 Einheiten der Ware x1 produzieren und maximal 300 Einheiten der Ware x2 .
Insgesamt kann die Firma maximal 400 Einheiten pro Tag produzieren.
Zuerst wird nun die Zielfunktion formuliert: Maximiere Gewinn (1 Euro pro , 6 Euro pro ) : .
Anschließend werden die Nebenbedingungen formuliert.
Maximal 200 Exemplare von x1
Maximal 300 Exemplare von x2
Insgesamt maximal 400 Exemplare
Es müssen Waren produziert werden
Der Punkt ist zulässig mit Funktionswert 0
Der Punkt ist zulässig mit Funktionswert 1400
Der Punkt ist zulässig mit Funktionswert 1900 und globales Maximum
Der Punkt ist unzulässig
Dieses Beispiel ist ein lineares Optimierungsproblem.
Beispiel Kürzester Weg
Bearbeiten
Es soll die Distanz von s nach y bestimmt werden. Dafür sollen folgende Variablen und Bezeichner betrachtet werden.
- : die Kante von a nach b ist Teil des kürzesten Pfades von s nach y für alle Kanten (a,b)
- : Das Gewicht der Kante von a nach b, zum Beispiel
- Die Zielfunktion ist
Es gelten folgende Nebenbedingungen:
- Die Gewichte müssen wie im Graph sein
- Alle Kanten (a,b) mit müssen einen Pfad von s nach y bilden:
- Es gibt genau eine Kante mit Startpunkt s:
- Es gibt genau eine Kante mit Zielpunkt y:
- Für jeden anderen Knoten gilt, falls eine Kante in diesen Knoten reinführt, muss er auch wieder eine rausführen, zum Beispiel für
Beachte durch die Minimierung werden Kreise auf dem Pfad automatisch verhindert.
Vollständiges Optimierungsproblem für ein kleines Beispiel von u nach x:

Das Problem der Kürzesten-Wegfindung ist ein ganzzahliges Optimierungsproblem, allgemeiner ein kombinatorisches Optimierungsproblem.
Problemklassen
BearbeitenOptimierungsprobleme sind unterschiedlich schwer lösbar
- lineare Probleme: f,h sind linear, z.B. f/x,y)=3x+4y. Diese sind einfach zu lösen
- Quadratische Probleme: z.B. sind auch noch einfach zu lösen.
- Konvexe Probleme: z.B. min sind schon schwerer zu lösen.
- Nicht-konvexe Probleme: z.B. sind ziemlich schwer zu lösen.
- Ganzzahlige Probleme: sind überraschenderweise schwerer zu lösen als reelle Probleme. Etwa allgemeiner handelt es sich hier um kombinatorische Probleme (diskrete Elemente, nicht notwendigerweise Zahlen)
- Weitere Parameter
- Restringierte Probleme: zulässige Menge ist beschränkt
- Unrestringierte Probleme: zulässige Menge ist unbeschränkt
Hier werden wir uns aber nur mit linearer Optimierung befassen.
Kombinatorische Optimierung
BearbeitenAuf dieser Seite wird die kombinatorische Optimierung behandelt. Kombinatorische Optimierungsprobleme sind im allgemeinen sehr schwer. Beispielsweise das Travelling Salesman Problem, oder die Knotenüberdeckung( Vertex Cover). Allgemeine Algorithmen sind meist sehr ineffizient. Deswegen benutzt man meistens domänenspezifische Algorithmen, so wie bei unseren bisherigen Beispielen. Wir schauen und jetzt noch ein weiteres Beispiel an.
Das Rucksackproblem
BearbeitenHierbei handelt es sich um ein einfaches kombinatorisches Optimierungsproblem. Gegeben ist ein Rucksack mit der maximalen Kapazität C und n Gegenstände mit jeweils dem Gewicht und dem Wert . Gesucht wird die Auswahl der Gegenstände, so dass das Gesamtgewicht die Kapazität nicht überschreitet und die Summe der Werte maximal ist ist maximal. Es gibt dafür Möglichkeiten.
Generieren
Bearbeitenzunächst werden die Objekte generiert:
public class Ding {
public int gewicht, nutzen;
static private java.util.Random ra = new java.util.Random();
// generieren
Ding() {
gewicht = ra.nextInt(MAX_GEWICHT) + 1;
nutzen = ra.nextInt(MAX_NUTZEN) + 1;
}
}
Es werden statische Variablen für die Problembeschreibung genutzt. Das Gewicht und der Nutzen der Objekte werden in einem eindimensionalem Array der Größe anzahlObjekte erstellt.
public class Rucksack {
static int anzahlObjekte=10;
static ding [ ] auswahlObjekte = null;
…
Die Gewichte und Nutzwerte werden zufällig zwischen 1 und dem jeweiligem Maximalwert generiert.
static final int MAX_GEWICHT = 10;
static final int MAX_NUTZEN = 10;
Generierung der Auswahlobjekte:
static Ding [ ] erzeugeObjekte() {
Ding[] r = new Ding[anzahlObjekte];
for (int i = 0; i < anzahlObjekte; i++ ) {
r[i] = new ding();
}
return r;
}
…
Die Kapazität der Rucksäcke ist eine weitere statische Variable.
static int kapazitaet;
Eine willkürlich gewählte Initialisierung der Main Methode ist:
kapazitaet = (int) (anzahlObjekte * MAX_GEWICHT / 4);
Dadurch passen im Schnitt nur die Hälfte der Gegenstände in den Rucksack.
Nun wird ein Rucksack als Auswahl der vorgegebene Dinge Implementiert, hierbei handelt es sich um die einzige nicht statische Variable.
boolean[] auswahl = null;
Der Konstruktor zum Erzeugen einen leeren Rucksacks lautet:
Rucksack () {
auswahl = new boolean [anzahlObjekte];
for (int i = 0; i < anzahlObjekte; i++ ){
auswahl[i] = false;
}
}
Es gibt einen Copy-Konstruktor zum Erzeugen einer Kopie eines existierenden Rucksacks. Die toString() Methode wird zur Ausgabe eines Rucksacks benutzt. Eine Methode zum Berechnen des Gesamtgewichts und des Gesamtnutzens lautet zum Beispiel:
int gewicht () {
int g = 0;
for (int i=0; i < auswahl.length; i++ )
if (auswahl[i] == true)
g = g + auswahlObjekte[i].gewicht;
return g;
}
| Index i | 0 | 1 | 2 | 3 | 4 | 5 |
| Gewicht | 7 | 5 | 8 | 3 | 3 | 2 |
| Nutzen | 1 | 5 | 2 | 2 | 1 | 9 |
Rucksack 1 beinhaltet die Gegenstände 0,2 und 3, hatte ein Gesamtgewicht von 18 und einen Gesamtnutzen von 5.
| Rucksack 1 | T | F | T | T | F | F |
Rucksack 2 beinhaltet die Gegenstände 1,2 und 5, hatte ein Gesamtgewicht von 15 und einen Gesamtnutzen von 16.
| Rucksack 2 | F | T | T | F | F | T |
Das Rucksackproblem als Greedy Algorithmus
BearbeitenNun wird das Rucksackproblem mit dem Greedy Algorithmus gelöst. Wir erinnern uns, das Greedy-Grundprinzip ist es in jedem Berechnungsschritt die jeweils aktuell geeignetste Zwischenlösung zu verwenden. Angewandt auf unser Rucksackproblem bedeutet das, lege von den noch nicht im Rucksack befindlichen Gegenständen jeweils den „besten“ hinzu. Doch was ist der beste Gegenstand? Der nützlichste? Der leichteste? Der mit dem besten Verhältnis aus Nutzen und Gewicht?
Algorithmus nach Nutzen
Bearbeitenstatic Rucksack packeGierigNachNutzen() {
Rucksack r = new Rucksack();
while (true) {
int pos=-1; int besterNutzen = 0;
for (int i=0; i<auswahlObjekte.length; i++)
if (r.auswahl[i] == false &&
auswahlObjekte[i].nutzen > besterNutzen &&
r.gewicht() + auswahlObjekte[i].gewicht <=
kapazitaet) {
besterNutzen = auswahlObjekte[i].nutzen;
pos = i;
}
if (pos == -1) break;
else r.auswahl[pos] = true;
}
return r;
}
Algorithmus nach Gewicht
Bearbeitenstatic Rucksack packeGierigNachGewicht() {
Rucksack r = new Rucksack();
while (true) {
int pos=-1; int bestesGewicht = MAX_GEWICHT+1;
for (int i=0; i<auswahlObjekte.length; i++)
if (r.auswahl[i] == false &&
auswahlObjekte[i].gewicht < bestesGewicht &&
r.gewicht() + auswahlObjekte[i].gewicht <=
kapazitaet) {
bestesGewicht = auswahlObjekte[i].gewicht;
pos = i;
}
if (pos == -1) break;
else r.auswahl[pos] = true;
}
return r;
}
Aufruf in main()
Bearbeitenpublic static void main (String args[]) {
if (args.length == 1)
anzahlObjekte = Integer.parseInt(args[0]);
kapazitaet = (int) (anzahlObjekte * MAX_GEWICHT / 4);
auswahlObjekte = erzeugeObjekte();
Rucksack r1 = packeGierigNachGewicht();
System.out.println(„Greedy Gewicht: „ + r1);
Rucksack r2 = packeGierigNachNutzen();
System.out.println(„Greedy Nutzen: „ + r2);
…
Analyse
BearbeitenDer Vorteil ist der relativ geringe Berechnungsaufwand durch die quadratische Komplexität . Das Problem ist aber, dass nicht die optimale Lösung gefunden wird.
Rucksackproblem als Backtracking
BearbeitenNun wird das Rucksackproblem mit Backtracking gelöst. Das Grundprinzip ist es, die optimale Lösung durch systematisches Absuchen des gesamten Lösungsraums zu finden. Angewandt auf unser Rucksackproblem bedeutet das, es gibt verschiedene Möglichkeiten, wir generieren und testen alle möglichen Rucksäcke und wir wenden Rekursion an.
Rekursionseinstieg
Bearbeitenstatic Rucksack packeOptimalmitBacktracking() {
return rucksackRekursiv(0, new Rucksack());
}
- Erster Parameter: Level i – Entscheidung, ob Objekt i in den Rucksack kommt
- Durchlaufen des Auswahl-Arrays von links nach rechts
- Aufrufgraph: Aufspannen eines binären Baumes durch ja/nein-Entscheidungen
Rekursion
Bearbeitenstatic rucksackRekursiv(int i, Rucksack r) {
if (i==auswahlObjekte.length) return r;
// Objekt i nicht nehmen und rekurrieren
Rucksack r1 = new Rucksack(r);
r1 = rucksackRekursiv(i+1, r1);
// Objekt i – falls moeglich – nehmen und rekurrieren
if (r.gewicht()+auswahlObjekte[i].gewicht<=kapazitaet){
Rucksack r2 = new Rucksack(r);
r2.auswahl[i] = true;
r2 = rucksackRekursiv(i+1,r2);
// Den besseren Rucksack immer zurueckgeben
if (r2.nutzen() > r1.nutzen())
return r2;
}
return r1;
}
Analyse
BearbeitenDas Problem ist hier, dass es einen extrem hohen Berechnungsaufwand für die große Auswahl an Objekten gibt. Die Komplexität liegt bei . Der Vorteil ist, dass man garantiert die optimale Lösung finden, da im schlimmsten Fall jede Möglichkeit ausprobiert wird. Also wird in jedem Fall ein Optimum gefunden.
Rucksackproblem als dynamische Programmierung
BearbeitenNun wird das Rucksackproblem mit dynamischer Programmierung gelöst. Wir erinnern uns, dass das Grundprinzip der dynamischen Programmierung die Wiederverwendung von bereits berechneten Teillösungen ist. Aber an dieser Stelle ist Vorsicht geboten mit den anderen Lösungen aus den vorherigen Seiten, wo Teillösungen Bottom up zusammengesetzt wurden. Hier basieren die Lösungen auf der Backtracking Variante. Teillösungen werden zwischengespeichert. Die Existenz von Teillösungen wird als Abbruchkriterium für die Rekursion verwendet.
Rekursionseinstieg
Bearbeitenstatic Rucksack packeMitDynamischerProgrammierung()
Rucksack [][] zwischenErgebnisse=
new Rucksack[kapazitaet+1][anzahlObjekte];
return rucksackRekursivDP (0, new Rucksack(), zwischenErgebnisse);
}
Ein Eintrag zwischenErgebnisse[g][i] bedeutet, dass wir schon ein mal dabei waren, das Objekt i in einen Rucksack mit dem Gewicht g zu legen. In diesem Fall können wir alle vor berechneten Entscheidungen für die Objekte i bis anzahlObjekte −1 wiederverwenden, da diese bereits optimal sind (Backtracking: äquivalenter Teilbaum).
Rekursion
Bearbeitenstatic Rucksack rucksackRekursivDP (int i, Rucksack r, Rucksack [][] zwischenErgebnisse){
if (i == auswahlObjekte.length) return r;
int gewicht = r.gewicht();
// Wiederverwendung von Teillösungen:
if (zwischenErgebnisse[gewicht][i] != null}{
for (int j = i; j < anzahlObjekte; j++)
r.auswahl[j] = zwischenErgebnisse[gewicht][i].auswahl[j];
return r;
}
Rucksack r1 = new Rucksack (r);
r1 = rucksackRekursivDP(i+1, r1, zwischenErgbenisse);
if (gewicht+auswahlObjekte[i].gewicht <= kapazitaet){
Rucksack r2 = new Rucksack (r);
r2.auswahl[i] = true;
if (r2.nutzen() > r1.nutzen()) r1 = r2;
}
// Merken von Teillösungen:
zwischenErgebnisse[gewicht][i] = r1;
return r1;
}
Analyse
BearbeitenDie Vorteile der dynamischen Programmierung sind, dass auf jeden Fall die optimale Lösung gefunden wird. In vielen Fällen hat sie auch einen geringeren Aufwand als Backtracking. Das Problem ist allerdings, dass die Anwendbarkeit und der Aufwand abhängig von der Größe und der Struktur des Suchraums sind. Die Komplexität beträgt O(z), wobei z die Anzahl der möglichen Zwischenergebnisse ist. Zum Beispiel: bei vielen unterschiedlichen Gewichtskombinationen kaum Ersparnis (Erhöhen von MAX_GEWICHT). Außerdem existieren polynomielle Approximationen!
Lineare Optimierung
BearbeitenLineare Optimierung
BearbeitenAuf dieser Seite wird die lineare Optimierung behandelt. Eine lineare Optimierungsaufgabe ist: Maximiere eine lineare Funktion in mehreren Variablen
.
Die lineare Nebenbedingung sind gegeben als lineare Gleichungen:
...
Dies entspricht dem Gleichungssystem:
Doch ist das ausdrucksstark genug für unsere Probleme?
Umformung von Gleichungssystemen
BearbeitenBeliebige Systeme lassen sich in die Standardform übertragen.
- Minimieren ist wie maximieren:
- Bedingungen statt Bedingungen:
- Gleichung zu Ungleichung:
- Ungleichung zu Gleichung (Schlupfvariablen einführen):
- kann negativ sein:
Beispiel Gewinnmaximierung
BearbeitenEine Firma produziert zwei verschiedene Waren. Ware erbringt einen Gewinn von einem Euro. Ware erbringt einen Gewinn von 6 Euro. Die Frage hierzu lautet, welches Verhältnis von und führt zum größten Gewinn? Dazu gibt es zwei Nebenbedingungen:
- Die Firma kann täglich maximal 200 Einheiten der Ware produzieren und maximal 300 Einheiten der Ware
- Insgesamt kann die Firma maximal 400 Einheiten pro Tag produzieren
Die Firma beschließt eine weitere Ware zu produzieren.
- Die Ware bringt einen Gewinn von 13 Euro.
- Die maximale Tagesproduktion liegt weiterhin bei 400 Einheiten.
- Für die Produktion von Ware und Ware wird dieselbe Maschine verwendet, allerdings ist der Produktionsaufwand für dreimal höher. Insgesamt kann die Maschine 600 Arbeitsschritte leisten.
Formuliere, die Zielfunktion: .
Anschließend formuliere die Nebenbedingungen:

Die Nebenbedingungen definieren ein drei-dimensionales Polyeder, in dem die optimale Lösung liegt.
Nun formen wir in die Normalform um:

Die Nebenbedingungen definieren nun ein Polyeder, in dem die optimale Lösung liegt.

Die Zielfunktion ist eine Gerade. Nun wird die Gerade verschoben, bis das Maximum erreicht ist.
Die Linearen Optimierungsprobleme der Form
besitzen genau dann eine endliche Optimallösung, wenn sie eine optimale Ecklösung (= „Ecke“ des zugehörigen Polyeders) besitzen. D.h. man muss zur Lösungsfindung nur die Ecken des Polyeders betrachten.
Simplex Verfahren
BearbeitenSimplex Verfahren
BearbeitenAuf dieser Seite wird das Simplex Verfahren behandelt.
Idee
Bearbeiten
Es wird in einer beliebigen Ecke des Polyeders begonnen. Dann wird verglichen, ob einer der Nachbarn eine bessere Lösung für die Optimierung bietet und anschließend wird dieser Knoten betrachtet. Am Ende erreichen wir eine Ecke, die keinen Nachbarn mit einer besseren Lösung hat. Die Lösung ist nun ein lokales Optimum. Bei der linearen Optimierung gilt, dass ein lokales Optimum automatisch ein globales Optimum ist, da der Polyeder eine konvexe Menge ist. Graphisch kann mit dieser Idee jedes lineare Optimierungsproblem gelöst werden. Dies wird aber sehr schnell unübersichtlich (und kann schlecht implementiert werden). Wir benötigen eine einfache Charakterisierung der “Ecken” des Polyeders. Diese erhalten wir durch Betrachtung der Basen der Matrix A.
Das Simplex-Verfahren löst ein lineares Programm in endlich vielen Schritten oder stellt seine Unlösbarkeit oder Unbeschränktheit fest. Im Worstcase hat es exponentielle Laufzeit unabhängig von den gewählten Pivotregeln, in der Praxis ist es sehr effizient. Das Simplex-Verfahren berechnet auch die Lösung für das duale Problem zu einem linearen Programm.
Wiederholung algebraischer Grundlagen
BearbeitenSeien .
- Die Linearkombination von mit den Koeffizienten ist der Vektor .
- Die Vektoren sind linear abhängig, wenn es ein gibt, so dass sich als Linearkombination von darstellen lässt.
- Eine maximale Menge linear unabhängiger Vektoren heißt Basis des zugehörigen Raumes. Eine Basis des besteht beispielsweise aus m linear unabhängigen Vektoren.
- Der Rang einer Matrix A ist die maximale Anzahl linear unabhängiger Spaltenvektoren.
Matrix lineares Optimierungsproblem
Bearbeiten
,
Da wir für jede unserer ursprünglichen Ungleichungen eine Schlupfvariable eingeführt haben, gilt stets Rang(A)=m (=Anzahl der Gleichungen=Länge des Vektors b).
Basis und Basislösung
BearbeitenAuf dieser Seite werden die Basen und Basislösungen beim Simplex Verfahren behandelt. Gegeben ist ein lineares Gleichungssystem .
Dann bilden m lineare unabhängige Spaltenvektoren aus A eine Basis von A. Diese wird mit bezeichnet. B enthält die Indices der Basisvektoren. N enthält die Indices der Nichtbasisvektoren. Die Basislösung ist gegeben durch: dies gilt genau dann wenn: . ist eine zulässige Basis von A, wenn gilt . Wenn ist, dann ist es eine zulässige Basislösung von A.
Beispiel 1
Bearbeiten
Nicht-Basisvariablen werden stets auf 0 gesetzt. Die zulässige Basislösung von A mit Zielfunktionswert 0, die man durch einsetzen erhält ist dann (0,0,200,300,400).
Beispiel 2
Bearbeiten
Nicht-Basisvariablen werden stets auf 0 gesetzt.
Die zulässige Basislösung von A, die man durch einsetzen erhält ist dann (200,0,0,300,200) mit dem Zielfunktionswert 200.
Basen von A
BearbeitenHier gibt es eine Übersicht der Basen von A mit dessen zulässigen Lösungen.
| x | |||
Basen von A- mit unzulässigen Lösung
BearbeitenHier gibt es eine Übersicht der Basen von A mit unzulässigen Lösungen.
| x | |||
Diese Basen haben keine zulässige Lösungen, da negative Werte enthält.
Die Teilmengen von A sind keine Basen von A, da die Vektoren jeweils linear abhängig sind.
Charakterisierung von Polyederecken
BearbeitenWarum schauen wir uns Basen und Basislösungen an? Wir waren doch an Ecken des Polyeders interessiert...
Sei das System gegeben, . Dann sind äquivalent:
- x ist eine Ecke des zugehörigen Polyeders
- x ist eine zulässige Basislösung von Ax=b
Wir wissen, dass die optimale Lösung in einem Eckpunkt liegen muss, falls sie existiert. D.h. wir müssen nur über die Basen von A optimieren (diese bestimmen ja die zulässigen Basislösungen von Ax=b). Dies erfolgt mit sogenannten Tableaus.
Das Simplex-Verfahren besteht aus einer Folge von Basen bzw. Tableus.
- Zuerst wird die zulässige Basis gefunden und daraus das Starttableau konstruiert.
- Anschließend wir eine neue zulässige Basis aus konstruiert, so dass die zulässige Basislösung von besser ist, als die von . Das Tableau wird nun aktualisiert.
- Wenn es keine bessere Basislösung mehr gibt, dann ist die letzte optimal.
Ein Tableau entspricht dem Gleichungssystem mit .
ist ein Simplextableau zur Basis
mit
Beispiel Gewinnmaximierung
BearbeitenNun wird der Simplex Algorithmus anhand des Beispiels der Gewinnmaximierung Schritt für Schritt durchgegangen.
Zielfunktion:
.
Nebenbedingungen:
Das System lässt sich umschreiben zu:
Initialisierung
BearbeitenGestartet wird mit der Basislösung, die durch die Schlupfvariable gegeben ist.
Starttableau
Bearbeiten| b | ||||
| z | 1 | 6 | 13 | 0 |
| 1 | 0 | 0 | 200 | |
| 0 | 1 | 0 | 300 | |
| 1 | 1 | 1 | 400 | |
| 0 | 1 | 3 | 600 |
sind Nichtbasiselemente, Z ist die Zielfunktion und sind Basiselemente. Dabei sind die blau hinterlegten Felder das , die gelb hinterlegten Felder stellen den Teil von dar und die grünen Felder sind . Das nicht markierte Feld ist dabei der negative Zielfunktionswert .
Update eines Tableau
BearbeitenFür das Update eines Tableau wird eine neue zulässige Basis bestimmt, indem ein Basisvektor durch einen Nichtbasisvektor ausgetauscht wird. Die Menge der Nichtbasisvektoren, die getauscht werden können, ist über die positiven Koeffizienten c der Zielfunktion definiert als: . Wenn dann breche ab und gebe x zurück. Die Menge der Basisvektoren, die getauscht werden können, ist über ihre j-te Komponente bestimmt: . Wenn für alle dann ist das LP unbeschränkt, da die Zielfunktion durch unbeschränkt wächst.
Optimierungsphase
BearbeitenBerechne für eine zulässige Basis, das zugehörige Tableau. Nun wird E bestimmt. Wenn dann wird abgebrochen und x zurückgegeben. Ansonsten wird durch eine geeignete Pivotregel gewählt. Als nächstes wird bestimmt. Wenn dann wird zurückgegeben, dass LP unbeschränkt ist. Ansonsten wird durch eine geeignete Pivotregel gewählt. Führe nun einen Basiswechsel durch und starte wieder oben.
Beispiel
Bearbeiten| b | ||||
| z | 1 | 6 | 13 | 0 |
| 1 | 0 | 0 | 200 | |
| 0 | 1 | 0 | 300 | |
| 1 | 1 | 1 | 400 | |
| 0 | 1 | 3 | 600 |
Heuristik für die Auswahl der Tauschvektoren
BearbeitenAls erstes werden die größten Koeffizienten in der Zielfunktion gewählt (Dantzig). Eine andere Möglichkeit ist das steepest-edge pricing, welches die Kombination aus Spalten- und Zeilenvektor wählt, die den größten Zuwachs für die Zielfunktion bringt. Oder der kleinste Index wird gewählt. Die letzte Möglichkeit ist eine zufällige Auswahl.
Erste Iteration
BearbeitenHeuristik: Ersetze einen Basisvektor durch den Nichtbasisvektor, der den größten Zugewinn für die Zielfunktion bringt.
Hier wird die Zeile von betrachtet und die Spalte von . Der alte Wert ist 0. Der Koeffizient von in der Zielfunktion ist 1 und der Zugewinn durch ist 200.
Hier wird die Zeile von betrachtet und die Spalte von . Der alte Wert ist 0. Der Koeffizient von in der Zielfunktion ist 6 und der Zugewinn durch ist 1800.
Hier wird die Zeile von betrachtet und die Spalte von . Der alte Wert ist 0. Der Koeffizient von in der Zielfunktion ist 13 und der Zugewinn durch ist 2600. Nun wird durch ersetzt.
Update des Tableaus
BearbeitenDer neue Wert von wird nun berechnet.
.
Dieser Wert wird nun eingesetzt.
Das neue Tableau sieht nun so aus:
| b | ||||
| z | 1 | -2600 | ||
| 1 | 0 | 0 | 200 | |
| 0 | 1 | 0 | 300 | |
| 1 | 200 | |||
| 0 | 200 |
Was haben wir nun gemacht? Von der Basis haben wir zu der Basis gewechselt und zu der neuen Basis haben wir das entsprechende Tableau bestimmt.
Zweite Iteration
Bearbeiten
Heuristik: Ersetze einen Basisvektor durch den Nichtbasisvektor, der den größten Zugewinn für die Zielfunktion bringt.
Hier wird die Zeile von betrachtet und die Spalte von . Der alte Wert ist 2600. Der Koeffizient von in der Zielfunktion ist 1 und der Zugewinn durch ist 200.
Hier wird die Zeile von betrachtet und die Spalte von . Der alte Wert ist 2600. Der Koeffizient von in der Zielfunktion ist 6 und der Zugewinn durch ist 1800. Nun wird durch ersetzt.
Update des Tableaus
BearbeitenDer neue Wert von wird nun berechnet.
. Dieser Wert wird nun eingesetzt.
Das neue Tableau sieht nun so aus:
| b | ||||
| z | 1 | -3100 | ||
| 1 | 0 | 0 | 200 | |
| 0 | 1 | 0 | 300 | |
| 1 | 0 | |||
| 0 | 100 |
Dritte Iteration
Bearbeiten
Ersetze einen Basisvektor durch den Nichtbasisvektor, der den größten Zugewinn für die Zielfunktion bringt. Es müssen nur Terme aus z mit positivem Vorzeichen betrachtet werden, d.h. es bleibt nur noch übrig.
Update des Tableaus
BearbeitenNun wird durch ersetzt.
. Dieser Wert wird nun eingesetzt.
Das neue Tableau sieht nun so aus:
| b | ||||
| z | -1 | -1 | -4 | -3100 |
| -1 | 200 | |||
| 0 | 1 | 0 | 300 | |
| 1 | 0 | |||
| 0 | 100 |
Die Zielfunktion kann nun nicht weiter verbessert werden. Unser x ist nun (0,300,100) und unser z ist 3100.
Analyse
BearbeitenDas Simplex-Verfahren löst ein lineares Programm in endlich vielen Schritten oder stellt seine Unlösbarkeit oder Unbeschränktheit fest. Im Worstcare hat es eine exponentielle Laufzeit, unabhängig von den gewählten Pivotregeln. In der Praxis ist es sehr effizient.





































































































































![{\displaystyle [\![\alpha ]\!](z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb848426592d90f105ae6d3b79d42d3e75697043)



![{\displaystyle [\![\alpha _{1}]\!](Z)=Z\langle X\leftarrow 2\cdot Z(Y)+1\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f7294a5cfa1ea817926c3190ea90e9d8c72ab1)

![{\displaystyle [\![\alpha _{1}]\!](Z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91da70633e63d59300681dea9b52e66bc2791800)

![{\displaystyle [\![\alpha _{1}]\!](Z)=Z\langle X\leftarrow 2\cdot Z(X)+1\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3a0b3d96b21cabd8be76f2413adca8544380a6e)


![{\displaystyle [\![\alpha _{1};\alpha _{2}]\!](Z)=[\![\alpha _{2}]\!]([\![\alpha _{1}]\!](Z))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df4c1d381be508c4b405cda244729414af6df43a)

![{\displaystyle [\![if~B~then~\alpha _{1}~else~\alpha _{2}]\!](Z)=\left\{{\begin{array}{ll}[\![\alpha _{1}]\!](Z)&\quad falls~Z(B)=true\\\,[\![\alpha _{2}]\!](Z)&\quad falls~Z(B)=false\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c534c8d30a5bc312f117ae28faf7a8c614ec34a)
![{\displaystyle [\![while~B~do~\alpha ]\!](Z)=\left\{{\begin{array}{ll}Z&falls~Z(B)=false\\\,[\![while~B~do~\alpha ]\!]([\![\alpha ]\!](Z))&sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0912c6c9b25944bd7bc4495d308a007b15d20556)


![{\displaystyle [\![PROG]\!]W_{1}\cdot ...\cdot W_{n}\to V_{1}\cdot ...\cdot V_{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16b75075db1e0c22509095ef3c23775b3036195)
![{\displaystyle [\![PROG]\!](w_{1},...,w_{n})=(Z(Y_{1}),...,Z(Y_{m}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dad8cb1da184b101985049b4b6a1489d15a9c77e)
![{\displaystyle wobei~Z=[\![\alpha ]\!](Z_{0}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e11c27986b45937457680a7974360fb9b688530c)






![{\displaystyle [\![PROG]\!](w_{1},...,w_{n})=Z(Y_{1},...,Z(Y_{m}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb6d4b9b85cd936122da7c21013d35ec546d4da5)






![{\displaystyle [\![FAC]\!](x)=\left\{{\begin{array}{ll}x!&{\text{für}}~x~\geq 0\\1&sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ba4024d9901d73dd55c9c70d21089cd1a7fff87)

![{\displaystyle [\![FAC]\!](x)=\left\{{\begin{array}{ll}x!&{\text{für}}~x~\geq 0\\\bot &sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/219396152e8abdf77377c24e4fd9c488ddec9b12)


![{\displaystyle [\![FAC]\!]:int\to int}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfb789da8fe2e7be02c5850c13d0e701dc78150f)
![{\displaystyle [\![FAC]\!](w)=Z(Y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61d2bb477fb6afeb6285d47248f9f2200915a7d3)
![{\displaystyle Z=[\![\alpha ]\!](Z_{0})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea4ca6687b20b2d70b39578e565452b234180ab2)



![{\displaystyle =[\![\alpha ]\!](3,\bot )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d4a5403856c43b827f023ccee91b26114bfad7f)
![{\displaystyle =[\![Y:=1;while~\beta ]\!](3,\bot )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037335c75fff8f8d9729dc2363623a87cdaa9685)
![{\displaystyle =[\![while~\beta ]\!]([\![Y:=1]\!](3,\bot ))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fa446c627fe591c0ab64dde39f6fd08a0c99d14)
![{\displaystyle =[\![while~\beta ]\!](3,\bot )Y\leftarrow 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/459643d9f6cc1f01550ff1b7c9ab107d3e7a0cc8)
![{\displaystyle =[\![while~\beta ]\!](3,1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddd7f5b84395f7118a8ec81ad6325df02821d42f)
![{\displaystyle =\left\{{\begin{array}{ll}Z&falls~Z(B)=false\\\,[\![while~B~do~\alpha ']\!]([\![\alpha ']\!](Z))&sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b82383538b003b765c607148ad34d6a8923e40f)
![{\displaystyle =\left\{{\begin{array}{ll}(3,1)&falls~Z(X>1)=(3>1)=false\\\,[\![while~\beta ]\!]~([\![Y:=Y\cdot X;~x:=X-1]\!](Z))&sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/674dc6ac4a60cc398a09019c73629904663c418f)
![{\displaystyle =[\![while~\beta ]\!]([\![Y:=Y\cdot X;~X:=X-1]\!](3,1))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f9ccd0ad622e97dfc4ba47ae5ff195a479e8e81)
![{\displaystyle =[\![while~\beta ]\!]([\![X:=X-1]\!]([\![Y:=Y\cdot X]\!](3,1)))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77163f22c498e0285a042b7e188796e52ad84aba)
![{\displaystyle =[\![while~\beta ]\!]([\![X:=X-1]\!](3,3))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9bb98a7cd897d02102943f7ae09666308de8f3d4)
![{\displaystyle =[\![while~\beta ]\!](2,3)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5acb9206dfc90dad004476ab1d9c7cbed3929fdc)
![{\displaystyle =\left\{{\begin{array}{ll}(2,3)&falls~Z(X>1)=(2>1)=false\\\,[\![(while~\beta )]\!]~([\![Y:=Y\cdot X;~X:=X-1]\!](Z))&sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1e0cf2772ce5143a87a174ac1be999000b93b20)
![{\displaystyle =[\![while~\beta ]\!]([\![Y:=Y\cdot X;~X:=X-1]\!](2,3))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab50e663d81fdf50e6884e6b0e638f9815348c9c)
![{\displaystyle =[\![while~\beta ]\!]([\![X:=X-1]\!]([\![Y:=Y\cdot X]\!](2,3)))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2735e2d4660104b81312c9e22995267918601d51)
![{\displaystyle =[\![while~\beta ]\!]([\![X:=X-1]\!](2,6))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9270f44a0e604f2a8235b9ce8a67c7c6d03d041)
![{\displaystyle =[\![while~\beta ]\!](1,6)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80dfb61a8347c03963e5e5e8fce5478ecd501345)
![{\displaystyle =\left\{{\begin{array}{ll}(1,6)&falls~Z(X>1)=(1>1)=false\\\,[\![(while~\beta )]\!]~([\![Y:=Y\cdot X;~X:=X-1]\!](Z))&sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e1abfd85cda0503400eeb3e8a351536a12d961b)

![{\displaystyle [\![FAC]\!](3)=Z(Y)=6}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b084ee327ecf82ab1df7ce14f71f068a55df57e2)
![{\displaystyle [\![FIB]\!](x)=\left\{{\begin{array}{ll}x-te~Fib.~Zahl&falls~x\geq 0\\0&sonst\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56db7f0087a6ba32b6fd38d8f4641a0fff49bfc8)
![{\displaystyle [\![GGT2]\!](x,y)=\left\{{\begin{array}{ll}ggT(x,y)&falls~x,y>0\\y&falls~x=y~\neq 0~oder~x=0,y\neq 0\\\bot &falls~y=0\\ggT(|x|,|y|)&falls~x<0~und~y>0\\-ggT(|x|,|y|)&falls~y<0\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dfc63094c84553002602a77d610d7c8edd86895)
![{\displaystyle i\in \{0,...,n-1\}~mit~b=A[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a71db61f40cc4120f56376913b0d03b8d4bc95a)













































































































































































































































































































































![{\displaystyle change[1],...,change[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f077dd5665e772f4632963297ddea31ebdbcfc0)
![{\displaystyle change[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bc4ef25f337b6a10d758211923a04a45faf34ae)


![{\displaystyle change[1]\cdot c_{1}+...+change[n]\cdot c_{n}=amount}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc7ede569279851b6a7bdc8935cf95329b83d026)
![{\displaystyle change[1]+...+change[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1928e469b3c511bf0e1e749ca3b4cdad55d51dff)













![{\displaystyle T_{k}^{[+n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67ca429626473c49cab7425d1606ac12bab810e8)

![{\displaystyle T_{k}^{[+n]}:T_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fdc39e29fa881987e86a63ebcdc899e96737b13)








![{\displaystyle T_{k}^{[+n]}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5bd51a6a9115272a5287ea2f8fc9ce6b8ee80c1d)

















































































![{\displaystyle border[j]:=max_{a\leq k\leq j-1}\{k|pat[1...k-1]=pat[j-k+1...j-1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7939f59961b713709ba3e3955ceb37dea6611376)



![{\displaystyle sborder[j]=max_{1\leq k\leq j-1}\{k|pat[1...k-1]=pat[j-k+1...j-1]\land pat[k]\neq pat[j]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27295f5e6f5a9cfe77d097f376876bd69e9909dd)








































![{\displaystyle p\in [u,o]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbbbbffbc252be70b64e3ebca2b391ae5bd24b19)

























































































































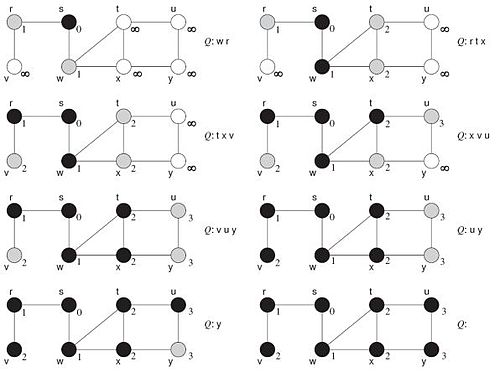












![{\displaystyle D[s]+\gamma (s,u)<D[u]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c738ddab1c09a24b922d405a821a042339ef1317)

![{\displaystyle \Rightarrow D[u]=10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71317c99dbf3d74df30200ee1693f2f3b3b427b5)
![{\displaystyle D[s]+\gamma (s,x)<D[x]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1f379f2308dd6ac3b8764fb38919f07e18d61eb)

![{\displaystyle \Rightarrow D[x]=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1b4a0320223418c33a7338081e03f0a4141161)

![{\displaystyle D[x]+\gamma (x,u)<D[u]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d4556cb5d2c3bfc966d2ef2ced8ce1efc25af76)

![{\displaystyle \Rightarrow D[u]=8}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331ce6731fa686c7b80487c3ac7454ab4eaa772a)
![{\displaystyle D[y]analog}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c32c7936bdfff2c96f467e84db2fc70c86592a)























![{\displaystyle D^{V'}[i,j]=fac(x):=\left\{{\begin{array}{ll}\gamma (i,j)&falls~k=0\\min\{D^{V'\backslash \{k\}}[i,j],D^{V'\backslash \{k\}}[i,k]+D^{V'\backslash \{k\}}[k,j]\}&falls~k\geq 1\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33f124e4ecac61a071702f5e26bb81979f2172e9)

![{\displaystyle D^{V'}[i,j]=\left\{{\begin{array}{ll}\gamma (i,j)&{\text{falls}}\ V'=\emptyset \\min\{D^{V'\backslash \{k\}}[i,j],D^{V'\backslash \{k\}}[i,k]+D^{V'\backslash \{k\}}[k,j]\}&{\text{für}}\ k\in V'\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbaf77bd5703a50998036270ecc76360729ad8fb)








































































































































































































































































































