Kurs:Diskrete Mathematik (Osnabrück 2020)/Arbeitsblatt 21
- Übungsaufgaben
Zeige, dass ein Graph, bei dem der Minimalgrad und der Maximalgrad gleich ist, ein Rundgang sein muss.
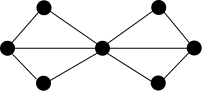
Finde im abgebildeten Graphen (mit der abgebildeten nicht optimalen Paarung und einer optimalen Paarung ) den im Satz von Berge postulierten alternierenden Weg und die dazugehörige optimale Paarung.
Der Satz behauptet, dass es bei einer nicht optimalen Paarung einen alternierenden Weg mit zwischen unabgedeckten verschiedenen Punkten gibt. Der Beweis zeigt, wie man einen solchen alternierenden Weg unter Verwendung einer optimalen Paarung findet und wie man damit die gegebene Paarung zu einer optimalen Paarung abändern kann. Das Beispiel ist besonders einfach, da es nur eine optimale Paarung gibt, nämlich diejenige, die aus den abstehenden Kanten besteht. Nennen wir diese . Wir bestimmen die symmetrische Differenz von und , diese besteht aus den drei Kanten links. Dies ist wie im Beweis des Satzes von Berge vorausgesagt eine alternierender Weg mit einer Kante aus (nämlich zwei Stück) mehr als Kanten aus (nämlich eine). Wir schmeißen aus die Dreieckseite links heraus und nehmen die zwei abstehenden Kanten hinzu und erhalten eine optimale Paarung (die in diesem Beispiel mit übereinstimmt).
Zeige, dass man im Satz von Berge nicht darauf verzichten kann, dass die Endpunkte der alternierenden Wege verschieden sind.
Es sei ein Graph und eine Teilmenge der Knotenmenge. Zeige, dass genau dann eine Knotenüberdeckung von ist, wenn gilt.
Bestimme die Knotenüberdeckungszahl zum Spielzuggraphen des Königs auf einem -Schachbrett.
Wir analysieren erst al den Graphen. Der Graph hat Knotenpunkte, wie man unmittelbar sieht. Der König kann um ein Feld in jede Richtung ziehen, horizontal, vertikal und diagonal. Entlang Die Anzahl der Kanten bestimmen wir entlang dieser Einteilung. Es gibt sechs horizontale, sechs vertikale und vier diagonale Kanten, also insgesamt Kanten. Eine Knotenüberdeckung muss all diese Kanten abdecken. Die Paarungszahl gibt eine erste Orientierung für die Knotenüberdeckungszahl, suchen wir also nach zueinander disjunkten Kanten. Da gibt es außen im Uhrzeigersinn vier Kanten, beginnend mit rechts oben und oben mittig. Die Paarungszahl ist also genau , da sie ja höchstens so groß wie die Hälfte der Punktanzahl sein kann. Somit ist die Knotenüberdeckungszahl zumindest . Wir behaupten, dass sie ist. Beispielsweise bildet der zentrale Punkt zusammen mit den weißen Feldern eine Knotenüberdeckung. Dies kann man sich mit einer Fallunterscheidung überlegen, ob der zentrale Punkt dazu oder nicht dazugehört.
Bestimme die Knotenüberdeckungszahl des abgebildeten Graphen.
Bestimme zu einem linearen Graphen der Länge die maximale Anzahl an Knoten in einer minimalen Knotenüberdeckung.
Charakterisiere diejenigen Graphen, deren Knotenüberdeckungszahl gleich ist.
Zeige, dass im abgebildeten Graphen jede minimale Knotenüberdeckung optimal ist.
Es sei ein bipartiter Graph mit einer Zerlegung . Zeige, dass die Knotenüberdeckungszahl von durch das Minimum der Anzahl von und der Anzahl von beschränkt ist.
Bestimme die Knotenüberdeckungszahl des Potenzmengengraphen zu einer dreielementigen Menge.
Wir betrachten Graphen
von der folgenden Bauart: Es gibt ein Zentrum , an das lineare Graphen (Strahlen) der Länge anliegen. Ansonsten gibt es keine weiteren Kanten.
- Skizziere einen solchen Graphen für
und
- Erstelle eine Formel für die Anzahl der Knoten und die Anzahl der Kanten von .
- Beschreibe eine minimale Knotenüberdeckung von , die enthält, und eine minimale Knotenüberdeckung, die nicht enthält.
- Bestimme die Knotenüberdeckungszahl von .
- Aufgaben zum Abgeben
Aufgabe (3 Punkte)
Finde im abgebildeten Graphen (mit der abgebildeten nicht optimalen Paarung und einer optimalen Paarung ) den im Satz von Berge postulierten alternierenden Weg und die dazugehörige optimale Paarung.
Aufgabe (3 Punkte)
Bestimme die Knotenüberdeckungszahl des abgebildeten Graphen.
Aufgabe (2 Punkte)
Bestimme die Knotenüberdeckungszahl des vollständigen Graphen .
Aufgabe (2 Punkte)
Bestimme die Knotenüberdeckungszahl des Potenzmengengraphen zu einer vierelementigen Menge.
| << | Kurs:Diskrete Mathematik (Osnabrück 2020) | >> |
|---|