Kurs:Diskrete Mathematik (Osnabrück 2020)/Arbeitsblatt 23

Übungsaufgaben

Aufgabe

1. Man gebe ein Beispiel für einen zusammenhängenden Graphen, der nicht hamiltonsch und eulersch ist.
2. Man gebe ein Beispiel für einen zusammenhängenden Graphen, der hamiltonsch und nicht eulersch ist.

Kommentar:

Die beiden Konzepte hamiltonsch und eulersch hören sich ähnlich an, deshalb besteht hier eine gewisse Verwechslungsgefahr. In beiden Begriffen geht es um geschlossene Wege in einem Graphen, d.h. Wege, wo der Anfangspunkt mit dem Endpunkt übereinstimmt. Nach Definition muss bei hamiltonsch jeder Knotenpunkt genau einmal auftreten und bei einem Eulerzug muss jede Kante genau einmal auftreten. Dies heißt bei einem Hamiltonkreis, dass dort nicht jede Kante vorkommen muss, allerdings folgt, dass jede Kante höchstens einfach vorkommt, da ja sonst auch die Randpunkte mehrfach vorkommen würden. Im eulerschen Fall können Punkte sowohl gar nicht als auch mehrfach vorkommen. Ein Rundgang ist gleichzeitig ein Hamiltonkreis und ein geschlossener Eulerzug. Einfache Beispiele, wo das eine, aber nicht das andere gilt, finden sich direkt auf den Aufgabenblättern 22 bzw. 23.

 

Aufgabe *

Zeige, dass der vollständige Graph ${}K_{4}$ nicht eulersch ist.

Aufgabe *

Bestimme die Anzahl der geschlossenen Eulerzüge in einem Rundgang.

Aufgabe

Bestimme die Anzahl der geschlossenen Eulerzüge im Schmetterlingsgraphen.

Aufgabe *

Zeige, dass es im Haus vom Nikolaus einen offenen, aber keinen geschlossenen eulerschen Kantenzug gibt.

Aufgaben zum Abgeben

Aufgabe (3 Punkte)

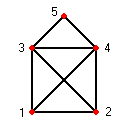
Bestimme die Anzahl der geschlossenen Eulerzüge im abgebildeten Graphen.