Kurs:Grundkurs Mathematik (Osnabrück 2018-2019)/Teil I/Vorlesung 4/kontrolle
- Quantoren
Betrachten wir nochmal die beiden Beispielaussagen
- Marsmenschen sind grün
- Ich fresse einen Besen,
und schauen uns die innere Struktur genauer an. In der ersten Aussage wird einer gewissen Art von Lebewesen eine Eigenschaft zugesprochen, so wie wenn man sagt, dass Geparden schnell sind oder dass Faultiere faul sind. Damit kann man meinen, dass Marsmenschen „im Normalfall“ oder „fast immer“ grün sind, oder aber im strengeren Sinn, dass wirklich alle Marsmenschen grün sind. In der Mathematik interessiert man sich für Aussagen, die ohne Ausnahmen gelten (wobei man allerdings in einer mathematischen Aussage die Ausnahmen auch explizit machen kann), sodass wir die Aussage im strengen Sinn verstehen wollen. Es handelt sich um eine sogenannte Allaussage. In ihr kommen zwei Prädikate (Eigenschaften, Attribute) vor, nämlich einerseits, ein Marsmensch zu sein, andererseits, grün zu sein. Ein Prädikat ist etwas, was einem Objekt (grammatisch spricht man von einem Subjekt), einem Gegenstand, einem Element zukommen oder nicht zukommen kann. Ein Prädikat ist für sich genommen keine Aussage; aus einem Prädikat kann man aber grundsätzlich auf zwei verschiedene Arten eine Aussage machen, indem man nämlich einerseits (durch einsetzen) für ein konkretes Objekt die Aussage
bildet, die bedeutet, dass das Objekt die Eigenschaft besitzt, was wahr sein kann oder eben auch nicht. Andererseits kann man daraus durch Quantifizierung eine Aussage gewinnen. So kann man die Aussage bilden, dass alle[1] Objekte (typischerweise aus einer bestimmten Grundmenge) die Eigenschaft haben, was wiederum wahr oder falsch sein kann. Das drückt man formallogisch durch
schreiben. Das bedeutet, dass für alle Objekte ohne weitere Einschränkung gilt: wenn es sich um einen Marsmenschen handelt (wenn also zutrifft), dann ist er auch grün. Für jedes steht in der großen Klammer eine Aussage in der Form einer Implikation, die eben besagt, dass wenn der Vordersatz wahr ist, dann auch der Nachsatz wahr sein muss.
Die zweite Beispielaussage kann bedeuten, dass ich genau einen Besen fresse oder aber mindestens einen Besen. Die Wortbedeutung des unbestimmten Artikels ist nicht eindeutig, in einer Aussage wie „eine Pflanze braucht Wasser“ bedeutet „eine“ sogar „alle“. In der Mathematik bedeutet es fast immer „mindestens einen“. Die Besenaussage kann man also paraphrasieren als
- Es gibt einen Besen, den ich fresse.
Dies ist eine Existenzaussage.[3] Eine formallogische Repräsentierung ist
wobei bedeutet, dass das Objekt ein Besen ist und wobei bedeutet, dass ich dieses fresse. Man könnte genauso gut
(oder Existenzoperator) genannt.
Eine Allaussage behauptet, dass ein gewisses Prädikat allen Objekten (aus einer gewissen Grundmenge) zukommt. Wie alle Aussagen kann dies wahr oder falsch sein. Eine Allaussage ist genau dann falsch, wenn es mindestens ein Objekt (aus der Grundmenge) gibt, dem das Prädikat nicht zukommt. Daher sind die beiden Quantoren, also der Allquantor und der Existenzquantor, über die Negation eng miteinander verknüpft und lassen sich gegenseitig ersetzen, und zwar gelten die Regeln
und
Neben einstelligen Prädikaten wie gibt es auch mehrstellige Prädikate der Form
die eine Beziehung zwischen mehreren Objekten ausdrücken, wie z.B. „ist verwandt mit“, „ist größer als“, „sind Eltern von“ u.s.w. Entsprechend kann dann über die verschiedenen Variablen quantifiziert werden, d.h. man hat mit Ausdrücken der Form
zu tun.
Die Variablenbezeichnung in einer quantifizierten Aussage ist grundsätzlich unwichtig, d.h. es ist egal, ob man oder schreibt. Man darf dabei aber nur Variablennamen (also Buchstaben) verwenden, die im gegenwärtigen Kontext nicht schon anderweitig verwendet sind.
Die Logik, die sich mit quantifizierten Aussagen auseinandersetzt, heißt Prädikatenlogik oder Quantorenlogik. Wir werden sie nicht systematisch entwickeln, da sie in der Mathematik als Mengentheorie auftritt. Statt , dass also ein Prädikat einem Objekt zukommt, schreiben wir , wobei dann die Menge aller Objekte bezeichnet, die diese Eigenschaft haben. Mehrstellige Prädikate treten in der Mathematik als Relationen auf.
- Mengen
Die Sprache der Mathematik wird in der Sprache der Mengen formuliert, die eng mit der Quantorenlogik verwandt ist.


Eine Menge ist eine Ansammlung von wohlunterschiedenen Objekten, die die Elemente der Menge heißen. Mit „wohlunterschieden“ meint man, dass es klar ist, welche Objekte als gleich und welche als verschieden angesehen werden. Die Zugehörigkeit eines Elementes zu einer Menge wird durch ausgedrückt, die Nichtzugehörigkeit durch . Für jedes Element(symbol) gilt stets genau eine dieser zwei Möglichkeiten. Die wichtigste mathematische Menge ist im Moment für uns die Menge der natürlichen Zahlen
Für Mengen gilt das Extensionalitätsprinzip, d.h. eine Menge ist durch die in ihr enthaltenen Elemente eindeutig bestimmt, darüber hinaus bietet sie keine Information. Insbesondere stimmen zwei Mengen überein, wenn beide die gleichen Elemente enthalten.
Unter der leeren Menge versteht man diejenige Menge, die kein Element besitzt. Sie wird mit
bezeichnet.
Eine Menge heißt Teilmenge einer Menge , wenn jedes Element aus auch zu gehört. Man schreibt dafür (manche schreiben dafür ). Beispielsweise ist die Menge aller durch teilbaren natürlichen Zahlen eine Teilmenge der Menge aller geraden Zahlen. Bei einer Teilmengenbeziehung sagt man auch, dass eine Inklusion vorliegt. Im Nachweis, dass ist, muss man zeigen, dass für ein beliebiges Element ebenfalls die Beziehung gilt.[4] Dabei darf man lediglich die Eigenschaft verwenden. Im Beispiel würde man so argumentieren: ist eine durch teilbare Zahl. Daher kann man
mit einer gewissen natürlichen Zahl schreiben. Dies kann man als
schreiben, was eben bedeutet, dass gerade ist.
Aufgrund des Extensionalitätsprinzips hat man das folgende wichtige Gleichheitsprinzip für Mengen, dass
gilt. In der mathematischen Praxis bedeutet dies, dass man die Gleichheit von zwei Mengen dadurch nachweist, dass man (in zwei voneinander unabhängigen Teilargumentationen) die beiden Inklusionen zeigt. Dies hat auch den kognitiven Vorteil, dass das Denken eine Zielrichtung bekommt, dass klar die Voraussetzung, die man verwenden darf, von der gewünschten Schlussfolgerung, die man aufzeigen muss, getrennt wird. Hier wiederholt sich das Prinzip, dass die Äquivalenz von zwei Aussagen die wechselseitige Implikation bedeutet, und durch den Beweis der beiden einzelnen Implikationen bewiesen wird.
- Beschreibungsmöglichkeiten für Mengen
Es gibt mehrere Möglichkeiten, eine Menge anzugeben. Die einfachste ist wohl, die zu der Menge gehörenden Elemente aufzulisten, wobei es auf die Reihenfolge der Elemente nicht ankommt. In der Abgabegruppe sind die Personen . Dies sind genau die Personen, die Sonntags im Schwimmbad morgens um Uhr am Tisch unter der Ulme sitzen. Es handelt sich dann um zwei verschiedene Beschreibungen für die gleiche Menge.
Die wichtigste Beschreibung einer Menge ist die durch eine Eigenschaft. Es sei eine Grundmenge gegeben (wie die Menge der natürlichen Zahlen, die Leute im Kurs) und ferner eine gewisse Eigenschaft (Prädikat), die man auf alle Elemente der Grundmenge sinnvoll anwenden kann und die auf manche Elemente zutrifft, auf manche nicht (wie gerade zu sein oder sich auf die Weihnachtsferien zu freuen). Zu der Eigenschaft gehört innerhalb von die Teilmenge bestehend aus allen Elementen aus , die diese Eigenschaft, diese Bedingung, erfüllen. Man beschreibt eine durch eine Eigenschaft definierte Teilmenge meist als
Dies geht natürlich nur mit solchen Eigenschaften, für die die Aussage eine wohldefinierte Bedeutung hat. Wenn man eine solche Teilmenge einführt, so gibt man ihr häufig sofort einen Namen (in dem auf die Eigenschaft Bezug genommen werden kann, aber nicht muss). Z.B. kann man einführen
Für die Mengen in der Mathematik sind meist eine Vielzahl an mathematischen Eigenschaften relevant und daher gibt es meist auch eine Vielzahl an relevanten Teilmengen. Aber auch bei alltäglichen Mengen, wie etwa die Menge der Studierenden in einem Kurs, gibt es viele wichtige Eigenschaften, die gewisse Teilmengen festlegen, wie etwa
Die Menge ist dabei selbst durch eine Eigenschaft festgelegt, es ist ja
- Mengenoperationen
So, wie man Aussagen zu neuen Aussagen verknüpfen kann, gibt es Operationen, mit denen aus Mengen neue Mengen entstehen.[5]
Zu Mengen und heißt
der Durchschnitt (oder die Schnittmenge) der beiden Mengen.
Zu zwei Mengen und heißt
die Vereinigung der beiden Mengen.
Zu Mengen nennt man
die Differenzmenge „ ohne “.
Diese Operationen ergeben nur dann einen Sinn, wenn die beteiligten Mengen als Teilmengen in einer gemeinsamen Grundmenge gegeben sind. Dies sichert, dass man über die gleichen Elemente spricht. Häufig wird diese Grundmenge nicht explizit angegeben, dann muss man sie aus dem Kontext erschließen. Ein Spezialfall der Differenzmenge bei einer gegebenen Grundmenge ist das Komplement einer Teilmenge .
Dafür schreibt man auch . Es gilt
und
Beispielsweise ist das Komplement der Menge der geraden Zahlen die Menge der ungeraden Zahlen. Die Eigenschaft, dass der Durchschnitt von zwei Mengen leer ist, bekommt einen eigenen Namen.
Zwei Mengen und heißen disjunkt, wenn ihr Durchschnitt ist.
Wenn Teilmengen durch geeignete Prädikate definiert sind, so stehen die Mengenoperationen unmittelbar in Zusammenhang mit den logischen Operationen für die Prädikate. Wenn (in einer gewissen Grundmenge)
und
vorliegt, so ist
- Mengendiagramme
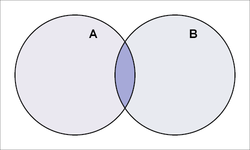
Eine Möglichkeit, Mengen oder vielmehr die zwischen verschiedenen Mengen möglichen oder existierenden Verhältnisse zueinander abzubilden, liefern Mengendiagramme (oder Venn-Diagramme). In ihnen werden Mengen durch gewisse Flächenstücke in der Ebene repräsentiert. Die Flächenstücke sollten eine möglichst einfache Form besitzen. Sie sind zumeist „zusammenhängend“ (d.h. je zwei Punkte des Stückes sind durch einen „stetigen Weg“ miteinander verbindbar). Die Flächenstücke können sich überlappen, und der Überlappungsbereich repräsentiert die Schnittmenge. Idealerweise sind die auftretenden Überlappungsbereiche selbst wieder zusammenhängend. Die verschiedenen Flächenstücke werden häufig in unterschiedlichen Farben oder Schraffuren gezeichnet, wobei dann die Überlappungsbereiche durch die zugehörigen Farbmischungen bzw. Mischschraffuren wiedergegeben werden.
Einige Beispiele für abstrakte Mengendiagramme
Diese Diagramme sind vollständig in dem Sinne, dass sie alle möglichen Schnitteigenschaften der beteiligten Mengen repräsentieren. In den folgenden Diagrammen wird nicht jede mögliche Schnitteigenschaft repräsentiert.
Einige Beispiele für konkrete Mengen-Diagramme
In diesem Fall repräsentieren die beteiligten Mengen einen bestimmten Begriff, das Schnittverhalten hängt dann von inhaltlichen Überlegungen ab. Solche Diagramme spielen in der Mathematik keine große Rolle. Wenn man allerdings z. B. verschiedene algebraische Begriffe wie Gruppe, Ring, kommutativer Ring, Divisionsbereich, Körper in ihrer Hierarchie veranschaulichen möchte, so ist ein solches Diagramm durchaus sinnvoll.
- Fußnoten
- ↑ Andere Formulierungen sind: jedes, ein beliebiges, irgendein Objekt/Element aus der Grundmenge. Wenn die Grundmenge räumlich ist, so spricht man auch von überall, wenn sie zeitlich ist, so spricht man von immer, stets, ....
- ↑ Man kann mit einiger Berechtigung sagen, dass die Vokabeln „für alle“ und „es gibt“ die wichtigsten Formulierungen der Mathematik sind.
- ↑ Neben „es gibt“ trifft man auf Formulierungen wie „es existiert“, „man findet“, „man kann finden“. Wenn die Existenz eines Objektes bekannt ist, so wird in einer mathematischen Argumentation häufig ein solches Element „hergenommen“, irgendwie bezeichnet und dann weiterverarbeitet.
- ↑ In der Sprache der Quantorenlogik kann man eine Inklusion verstehen als die Aussage .
- ↑ Man beachte, dass sich die ähnlich geformten Symbole und und und entsprechen.