Algebraische Kurven/Mechanische Kurven/Textabschnitt
Es sei eine feste Stange
(man denke an ein mechanisches Maschinenteil)
mit zwei fixierten Punkten
(man denke an Gelenke).
Diese Stange kann sich in der Ebene (dem ) bewegen, wobei die beiden Punkte sich jeweils in zwei bestimmten Bahnen
und
(man denke an Schienen)
befinden müssen. Die Bahnen können dabei recht einfach gegeben sein, etwa durch Geraden oder durch Kreise. Bei einer Dampfmaschine hat man ein drehbares Rad und eine gerade Schiene, die durch eine Stange gekoppelt sind. Wie beschreibt man den zugehörigen Bewegungsprozess? Was sind die erlaubten Konfigurationen des Systems?
Da eine solche Konfiguration durch die Lage der beiden Punkte bestimmt ist, und diese jeweils durch zwei Koordinaten der Ebene gegeben sind, handelt es sich insgesamt um eine vierdimensionale Situation.
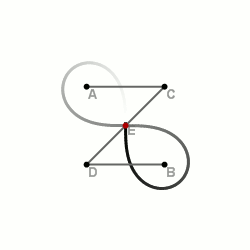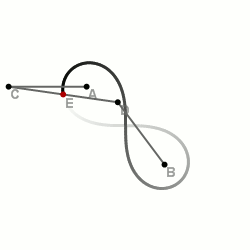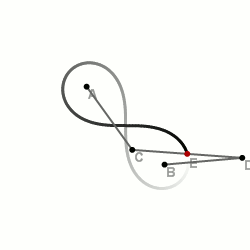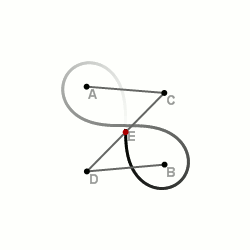
Wenn man einen Punkt der Stange fixiert (farblich markiert), wie sieht die Bewegungsbahn (oder Trajektorie) dieses Punktes in der Ebene aus?
Für die Extremfälle und sind die Bewegungsbahnen Teilmengen (in der Regel echte!) von und . Für Punkte dazwischen erwartet man eine stetige Deformation der einen Bahn in die andere.
Seien und zwei ebene algebraische Kurven, die durch die Gleichungen und beschrieben werden, . Es sei eine „bewegliche Gerade“ (eine Stange) mit zwei Punkten , , die voneinander den Abstand haben. Das mechanische System, das durch alle Lagen von in der Ebene gegeben ist, bei denen gleichzeitig und ist, wird folgendermaßen beschrieben.
Eine Lage der Stange in der Ebene ist eindeutig bestimmt, wenn für die beiden Punkte die Lage festgelegt ist (dies berücksichtigt noch nicht die Abstandsbedingung), also durch vier Variablen . Eine erlaubte Konfiguration muss dann die folgenden drei algebraischen Bedingungen erfüllen.
- (Abstandsbedingung)
Es handelt sich somit um drei algebraische Gleichungen in vier Variablen, als Lösungsmenge erwartet man also eine Kurve im . Ein Punkt wird durch den Abstand zu bzw. beschrieben. Da sich diese Punkte im mechanischen System bewegen, setzen wir die Koordinaten für den mitbewegten Punkt als
an (der Abstand von zu ist also ) und schreiben seine Koordinaten als
Man kann dann das gesamte mechanische System (durch eine lineare Transformation) in den vier Variablen ausdrücken, indem man bei ()
in den Gleichungen ersetzt. In den neuen Variablen erhält man die drei Gleichungen
- ,
- ,
Die zu gehörende Trajektorie kann man grundsätzlich dadurch erhalten, dass man aus diesem Gleichungssystem die Variablen und „eliminiert“, was eine algebraische Gleichung für und ergibt. Dies ist allerdings leichter gesagt als getan, häufig ist es sinnvoller, durch geschickte Manipulationen das Gleichungssystem zu vereinfachen.
Manchmal interessiert man sich auch für die Situation, wo sich mit der Stange eine ganze Ebene mitbewegt, und für die Trajektorien von solchen Punkten. Dies ist etwa der Fall, wenn auf der Stange weitere Maschinenteile montiert sind. In diesem Fall kann man jeden Punkt der Ebene bezüglich und als
Es wird also der Punkt als Ursprung der bewegten Ebene, die Verbindungsgerade zu als erste Koordinatenachse und die dazu senkrechte Achse als zweite Koordinatenachse genommen.
Das gesamte mechanische (Stangen-)System wird also durch vier Variablen mit drei Gleichungen beschrieben. Die sichtbare Wirkungsweise, nämlich der Bewegungsablauf eines fixierten Punktes auf , liefert aber eine Trajektorie in der affinen Ebene.










![{\displaystyle {}F_{1},F_{2}\in K[X,Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d18e0800e6622c05f7ed3b6255df68f4ace54b5e)
























