Projekt:Mathematik ist überall/Mengen/Lektionen/Mengenlehre

Mengen, Mengen, Mengen ... Diese Lektion soll die übliche Nomenklatur etwas lesbarer machen. Es ist also mehr „Lektura“ als „Klatura“.

Wichtige Mengen Es ist praktisch, einige Mengen als gegeben anzusehen, statt diese selbst herzuleiten. Die natürlichen Zahlen sind so eine Menge, bei der sich die Herleitung am Anfang nicht „lohnt“. Hier zunächst einmal die Mengen.

$\mathbb {N}$ Menge der natürlichen Zahlen Es ist oft erforderlich, anzugeben ob die 0 (Null) enthalten ist oder nicht. Eindeutig festgelegt ist weder das Eine noch das Andere. Eindeutig wird die Angabe durch $\mathbb {N} \setminus \,0\$  wenn die 0 (Null) nicht        enthalten sein soll. $0\in \mathbb {N} \$ wenn die 0 (Null) unbedingt enthalten sein soll. $\mathbb {Z}$ Menge der ganzen Zahlen. $\mathbb {Q}$ Menge der rationalen Zahlen. $\mathbb {A}$ Menge der algebraischen Zahlen Hier endet die Abzählbarkeit. $\mathbb {T}$ Menge der transzendenten Zahlen Hier beginnt die Überabzählbarkeit. $\mathbb {R}$ Menge der reellen Zahlen. $\mathbb {C}$ Menge der komplexen Zahlen.

Natürlich erschließen sich die Eigenschaften von Mengen oft erst durch ihre Erzeugung. Allerdings würde das diese Lektion sehr unübersichtlich machen. Hier erst einmal eine Übersicht der Hierarchien. Mit Hilfe des Symbols „ $\subset$ “ wird hier veranschaulicht, welche Menge echte Teilmenge welcher anderen ist. $\mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {A} \subset \mathbb {R} \$ Außerdem gilt noch $\mathbb {T} \subset \mathbb {R} \$ und $\mathbb {R} \subset \mathbb {C} \$ Die komplexen Zahlen bestehen jeweils aus zwei Komponenten, einem imaginären und einem reellen Anteil. Die Komponenten stehen im rechten Winkel zueinander. Die Menge der komplexen Zahlen bildet die Gaußsche Zahlenebene. Sie sind hier nur aufgeführt, um die Zahlenmengen komplett aufzulisten.

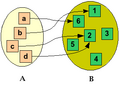
Elemente und Mengen Eine Menge besteht aus Elementen. Ein Element kann auch eine Menge sein. Gegeben sei die Menge $M=\{27\ d\ 4\}\$ Der Inhalt der Menge kann beschrieben werden: $27\in M\;,\ d\in M\;,\ 4\in M\$ Damit wird ausgedrückt, dass es sich bei 27, d und 4 um Elemente der Menge M handelt. Mehrere Elemente können auch zusammengefasst werden. Dabei muss aber genau auf die Schreibweise geachtet werden. $(27\;,\ d\;,\ 4)\in M\$ Im Folgenden sei die Menge $M=\{27\ \{x\ 3\ d\}\ 4\}\$ M enthält immer noch drei Elemente. Allerdings ist ein Element ebenfalls Menge (so wird mathematisch knapp ausgedrückt, dass es eine Eigenschaft des Elements ist, Menge zu sein). Für die mathematische Beschreibung des Mengeninhalts der Menge M gilt nun: $(27\;,\ \{x\ 3\ d\}\;,\ 4)\in M\$ Es gilt nicht, dass $\{x\ 3\ d\}\$ Teilmenge von M ist. Das Element „3“ aus dem Mengenelement ist kein Element der Menge M. Ausgedrückt wird diese Tatsache durch $3\notin \{27\ \{x\ 3\ d\}\ 4\}$

Mengen aus Mengen Die Inhalte von Mengen können selbst als Menge zusammengefasst werden. Es sind dann Teilmengen. Die naive Mengenlehre unterliegt der Zermelo-Fraenkel-Axiomatik nur mit Einschränkungen. Deshalb wird hier streng zwischen Teilmenge und echter Teilmenge unterschieden. So sind die beiden Aussagen $\{2\}\subset \{1\ 2\ \{1\ 2\ 3\}\}\$ und $\{2\}\subseteq \{1\ 2\ \{1\ 2\ 3\}\}\$ wahr. Wahr ist auch $\{1\ 2\ \{1\ 2\ 3\}\}\subseteq \{1\ 2\ \{1\ 2\ 3\}\}\$ aber $\{1\ 2\ \{1\ 2\ 3\}\}\subset \{1\ 2\ \{1\ 2\ 3\}\}\$ nicht. In der naiven Mengenlehre enthält jede Menge sich selbst als Teilmene. Es gilt aber auch, dass echte Teilmenge jede Teilmenge der Menge ist, außer der Menge selbst. Die Zermelo-Fraenkel-Axiomatik lässt die Bildung von Mengen, die sich selbst enthalten, nicht zu. Auf diese Tatsache wird hier nur hingewiesen, denn das Problem tritt nur sehr selten auf. Es gibt andere Axiomatiken (auch nicht naive), die nicht dieser (dafür aber anderen) unterliegen. Am einfachsten ist es, bei Relationen auf Echtheit zu achten.

Mengen mit Potenzial Mit Potenzial sind hier potentielle Möglichkeiten gemeint. Bei einer gegebenen Menge versteht sich dieser Begriff als Antwort auf die Frage: „Was könnte aus dieser Menge noch gebildet werden?“ Damit ist die Menge aller Teilmengen gemeint, die in der gegebenen Menge vorhanden sind. Die Bezeichnung dafür ist Potenzmenge. Bei Mengen von größerer Mächtigkeit artet die Ermittlung in Arbeit aus. Mathematiker verabscheuen Tätigkeiten, die auf Wiederholungen von einfachen Vorgängen beruhen. Hier ist eine derartige Tätigkeit erforderlich. Stattdessen formulieren sie lieber (sehr kurz) was zu tun ist. Die Potenzmenge der Menge $M=\{a\ b\ c\}$ ist ${\mathcal {P}}(M)=\{\{\}\ \{a\}\ \{b\}\ \{c\}\ \{a\ b\}\ \{a\ c\}\ \{b\ c\}\ \{a\ b\ c\}\}$ Die Potenzmenge enthält auch die leere Menge und die Ausgangsmenge als Element.

Leere Menge Die leere Menge hat eine Sonderstellung. So gilt für jede Menge M $\{\}\subseteq M$ Es ist wirklich jede Menge gemeint, also auch die leere Menge. Damit ist natürlich nicht gesagt, dass die leere Menge auch Element jeder Menge ist. Entsprechend der Zermelo-Fraenkel-Axiomatik gibt es genau eine leere Menge „Ø“ (Ø = {}). Um zwei gegebene Mengen auf Gleichheit zu überprüfen, muss ein gewisser Aufwand betrieben werden. „Zwei Mengen sind genau dann gleich, wenn ihre Elemente gleich sind (ZF-Axiom: EXT).“ Nun haben aber leere Mengen keine Elemente. Es müssen die Potenzmengen gebildet werden. Seien A und B zwei Mengen ohne Elemente. Damit gilt für ${\mathcal {P}}(A)=\{\{\}\}=\{\varnothing \}\$ und für ${\mathcal {P}}(B)=\{\{\}\}=\{\varnothing \}\$ Noch ein wenig „mathematische Folklore“ in Form von „Sind zwei Größen einer Dritten gleich, so sind sie auch einander gleich.“ Das ist bei den Potenzmengen von A und B gegeben und damit auch für die Ausgangsmengen.

Mengen vergleichen und bearbeiten Um Mengen vergleichen zu können, werden sie zueinander in Relation gesetzt. Abgesehen von Größenvergleichen, die bei Zahlen wichtig sind, gibt es in der Mengenlehre noch inhaltliche Vergleiche. Der Sammelbegriff für beide Arten lautet „Mengenrelationen“.

Element einer Menge Ob „etwas“ Element einer Menge ist, wird durch den Relativoperator $\in \$ ermittelt. Die Relation ist asymmetrisch in ihrer Formulierung und in ihrer Anwendung. Die Schreibweise $7\in \{B\ 6\ 8\ v\}\$ ist formal korrekt, aber $\{B\ 6\ 8\ v\}\in 7\$ ist formal unkorrekt, weil „7“ keine Menge ist. Eine korrekte Formulierung wäre mit $\{B\ 6\ 8\ v\}\in \{7\}\$ gegeben. Für die Ergebnisfindung gilt zwar in diesem Fall die Gleichheit, also: $\left(\{B\ 6\ 8\ v\}\in \{7\}\right)=\left(\{7\}\in \{B\ 6\ 8\ v\}\right)$ aber es gilt nicht, dass $\left(\{B\ 6\ 8\ v\}\in \{7\}\right)\Rightarrow \left(\{7\}\in \{B\ 6\ 8\ v\}\right).$ Es kann vorkommen, dass beide Relationen gleiche Ergebnisse liefern, aber daraus zu folgern, dass es auch andersrum geht ist falsch. Enthaltensein Elemente sind in (nicht leeren) Mengen enthalten. Die Aufzählung, dass das Element „a“, das Element „b“ usw. zu einer bestimmten Menge gehören, ist – wie unter Elemente und Mengen zu sehen – sehr schreibaufwendig. Einfacher ist es, die betreffenden Elemente ihrerseits zu einer Menge zusammenzufassen. So ist $\{6\ v\}$ eine Teilmenge von $\{B\ 6\ 8\ v\}$. Es ist sogar eine echte Teilmenge. Formal korrekt wird das so aufgeschrieben: $\{6\ v\}\subset \{B\ 6\ 8\ v\}$ Andererseits ist $\{B\ 6\ 8\ v\}$ auch eine Teilmenge – aber eben keine echte. Geschrieben wird das als: $\{B\ 6\ 8\ v\}\subseteq \{B\ 6\ 8\ v\}$. Es scheint fast selbstverständlich, dass die Mächtigkeiten der Teilmengen nicht größer sein können, als die Mächtigkeit der Ausgangsmenge. Sei M die Ausgangsmenge, dann gilt für Mächtigkeit die Teilmengen $|T_{i}|\leq |M|\,;\ i=1...|{\mathcal {P}}(M)|$ Es ist aber dennoch und durchaus der Erwähnung wert, wie der folgende Abschnitt zeigen wird. Denn die gemachte Überlegung zu den Mächtigkeiten ist in dieser Form leider nur für endliche Mengen sinnvoll.

Gleichheit Wenn zwei Mengen auf Gleichheit untersucht werden, werden in der naiven Mengenlehre zuerst die Mächtigkeiten verglichen und nach Feststellung der Übereinstimmung die einzelnen Elemente. Diese Vorgehensweise ist bei abzählbar unendlichen Mengen natürlich unmöglich. Das Attribut „abzählbar“ hat mit dem „Zählen der Elemente“ übrigens nichts zu tun. Allgemein gilt für die Gleichheit zweier Mengen A und B: $A=B\Leftrightarrow (A\subseteq B)\land (B\subseteq A)$ Damit wird ausgesagt: „‚A‘ und ‚B‘ sind genau dann gleich, wenn ‚A‘ Teilmenge von ‚B‘ ist und ‚B‘ Teilmenge von ‚A‘ ist.“ Diese Formulierung erscheint doch sehr übertrieben. Aber das ist nur der erste Eindruck. Es wird zwar nicht ausdrücklich gesagt, aber damit ist auch ein Vergleich der Mächtigkeiten verbunden. So können auch abzählbar unendliche Mengen verglichen werden. Die Vorgehensweise ist dann natürlich nicht mehr naiv zu nennen. Die Menge der natürlichen Zahlen ist genau so mächtig, wie die Menge der rationalen Zahlen. Der Grund dafür ist, dass alle rationalen Zahlen auf die natürlichen Zahlen abgebildet werden können. Das zeigte Cantor in seinem ersten Diagonalargument. Es gilt also $|\mathbb {Q} |=|\mathbb {N} |\$ und außerdem $\mathbb {N} \subset \mathbb {Q} \$. Weil aber $\mathbb {N} \neq \mathbb {Q} \$ zweifellos stimmt, müsste mindestens ein Element aus $\mathbb {Q} \$ nicht in $\mathbb {N} \$ enthalten sein. Dann wäre $\mathbb {Q} \$ aber nicht mehr abzählbar. Das ist ein Unterschied zwischen naiver und mathematischer Mengenlehre. Hilbert folgend, fällt die Entscheidung auf die Beibehaltung der paradiesischen Zustände.

Mengenoperationen Als Operation wird hier die Anwendung einer aktiven Handlung auf eine oder zwei Mengen verstanden. Es handelt sich also um eine Verknüpfung, dessen Resultat eine (neue) Menge ist. Die Regeln zur Anwendung der folgenden Operatoren ist in der (Mengen)algebra festgelegt.
Vereinigung $A\cup B\$ $A\cup B=C\$ Die Menge C enthält alle Elemente, die in Menge A oder in Menge B enthalten sind. $A=\{a\ b\}\,,\ B=\{a\ c\ d\}\$ $C=A\cup B=\{a\ b\}\cup \{a\ c\ d\}=\{a\ b\ c\ d\}\$	Schnitt $A\cap B\$ $A\cap B=C\$ Die Menge C enthält alle Elemente, die sowohl in Menge A als auch in Menge B enthalten sind. $A=\{a\ b\}\,,\ B=\{a\ c\ d\}\$ $C=A\cap B=\{a\ b\}\cup \{a\ c\ d\}=\{a\}\$
Differenz $A\setminus B\$ $A\setminus B=C\$ Einfach gesprochen: „ C ist A ohne B “. Die Menge C enthält die Elemente aus A, die nicht in B enthalten sind. $A=\{a\ b\ c\ d\ e\}\,,\ B=\{a\ b\ d\ f\ g\}\$ $C=A\setminus B=\{a\ b\ c\ d\ e\}\setminus \{a\ b\ d\ f\ g\}=\{c\ e\}\$	Komplement $A^{C}\$ Zur Bildung der Komplementmenge bedarf es einer Bezugsmenge, auf die sich das Komplement bezieht. Sei M die Bezugsmenge zu der das Komplement der Menge A gebildet wird, so ist das Ergebnis eine Teilmenge von M mit allen Elementen aus M, die nicht in A sind. $M=\{a\ b\ c\ d\ e\ f\}\$ $A=\{b\ c\ e\}\$ $A^{C}=\{a\ d\ f\}\$
Diskrepanz $A\Delta B\$ $A\Delta B=C\$ Die Menge C enthält alle Elemente, die entweder in der Menge A oder in der Menge B enthalten sind. $A=\{a\ b\ c\ d\ e\}\$ $B=\{c\ d\ e\ f\ g\}\$ $C=A\Delta B=\{a\ b\ c\ d\ e\}\Delta B\{c\ d\ e\ f\ g\}=\{a\ b\ f\ g\}\$	Produkt $A\times B=C\$ Die Menge C enthält die Menge aller geordneten Paare der Mengen A und B. $A=\{a\ b\}\$ $B=\{y\ z\}\$ $C=A\times B=\{(a,y)\ (a,z)\ (b,y)\ (b,z)\}\$

Mengenalgebra Als Algebra werden hier die „Regeln für die Bearbeitung von Mengen“ bezeichnet. Die Bezeichnet lautet daher einfach „Mengenalgebra“.   Schnitt Vereinigung Idempotenz $A\cap A=A\$ $A\cup A=A\$ Kommutativ $A\cap B=B\cap A\$ $A\cup B=B\cup A\$ Assoziativ $A\cap \left(B\cap C\right)=\left(A\cap B\right)\cap C\$ $A\cup \left(B\cup C\right)=\left(A\cup B\right)\cup C\$ Distributiv $A\cap \left(B\cup C\right)=\left(A\cap B\right)\cup \left(A\cap C\right)\$ $A\cup \left(B\cap C\right)=\left(A\cup B\right)\cap \left(A\cup C\right)\$ Absorptionsgesetz $A\cup (A\cap B)=A\$ $A\cap (A\cup B)=A\$ De Morgan ${\left(A\cap B\right)}^{C}=A^{C}\cup B^{C}\$ ${\left(A\cup B\right)}^{C}=A^{C}\cap B^{C}\$ Eigenschaften einiger Zahlenmengen Die wichtigsten, weil am häufigsten genannten, Eigenschaften einiger bereits erwähnter Zahlenmengen sind hier kurz zusammengefasst. Zahlenmenge Eigenschaften $\mathbb {N} \$ Menge der natürlichen Zahlen. Abzählbar unendlich Mächtigkeit $|\mathbb {N} |=\aleph _{0}\$ Kardinalität aller abzählbaren Mengen. Mächtigkeit von $|{\mathcal {P}}(\mathbb {N} )|=2^{\aleph _{0}}\,;\ 2^{\aleph _{0}}\notin \mathbb {N} \$. Oft auch als erste transfinite Ordinalzahl $\omega \$ bezeichnet. Menge der finiten Ordinalzahlen. $\mathbb {R} \$ Menge der reellen Zahlen. Überabzählbar unendlich (Kontinuum) Mächtigkeit $|\mathbb {R} |=\aleph _{1}\$ Kardinalität der überabzählbaren Mengen erster Stufe. Mächtigkeit von $|{\mathcal {P}}(\mathbb {R} )|=2^{\aleph _{1}}=\aleph _{2}\$. $\mathbb {C} \$ Menge der komplexen Zahlen. Überabzählbar unendlich Mächtigkeit $|\mathbb {C} |=|\mathbb {R} \times \mathbb {R} |=\aleph _{1}\$. Mengen abbilden Abbildungen sind mathematische Illustrationen und damit abstrakt. Mathematiker brauchen nicht einmal eine bildliche Darstellung für eine Abbildung, ihnen genügen zwei Mengen. Eine Abbildung (im mathematischen Sinne) ist eine vorschriftsmäßige Zuordnung aller Elemente der einen Menge auf die Elemente einer anderen Menge. Wenn diese Mindestvoraussetzungen erfüllt sind, liegt eine Funktion vor. Elementare Eigenschaften von Abbildungen Eine Funktion $f:A\rightarrow B\$ ist surjektiv (franz. sur: auf), wenn jedes Element von B als Bild dient. Es ist also eine Abbildung von A auf B vorhanden. injektiv, wenn unterschiedliche Elemente von A auf unterschiedliche Elemente von B deuten. bijektiv, wenn die Funktion f sowohl injektiv als auch surjektiv ist. Die Mengen A und B haben eindeutige Korrespondenz.