Diffusion/Tabellenkalkulation/Aufbau

Die folgende Lerneinheit befasst sich mit der Erstellung einer Datei in LibreOffice Calc (Tabellenkalkulation), die eine Animation auf der rechten Seite durch die Visualisierung der Konzentration in unterschiedlichen Zeitschritten durch einzelne Tabelle realisiert. Dadurch können die einzelne mathematischen Berechnungen von einem Zeitschritt $t$ nach $t+1$ mathematisch modelliert werden.

Diffusion: Verteilungsmatrix für die 3x3-Umgebung

Bedingte Formatierung

Die bedingte Formatierung hat in der Tabellenkalkulation die folgenden Funktionen:

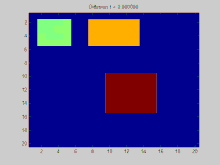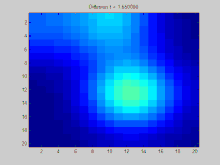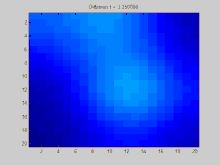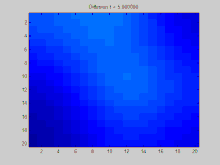
die Konzentrationsunterschiede durch unterschiedlich Farben zu kennzeichnen

rot=hohe Konzentration,
gelb=mittlere Konzentration,
grün=geringe Konzentration

Barrieren, Hindernisse und Begrenzungen mathematische (z.B. durch 0 bzw. 1) zu kodieren und in Abhängigkeit von dem Zelleintrag blau oder grau zu markieren.
bei sich bewegenden Objekten die Unterschiede in einzelnen Zellen zu kennzeichnen

-1 Mauer, Objekt oder Hinderniss wurde in dem Pixel entfernt (Heck des Autos befindet sich z.B. nicht mehr in dem Pixel)
0 keine Veränderung im Pixel
+1 Mauer, Objekt oder Hinderniss wurde in dem Pixel hinzugefügt (Front des Autos ist z.B. in das Pixel hineingefahren).

SUMMENPRODUKT - Erweitertes Skalarprodukt

Die mathematischen Grundlagen des Summenproduktes werden ausgehend vom Skalarprodukt für mehrere Matrizen definiert. Durch die Erweiterung kann man die erweiterte Definition für mehrere Matrizen nicht mehr als Skalarprodukt bezeichnen, weil die Axiome eines Skalarproduktes nicht mehr erfüllt werden. Das SUMMENPRODUKT ist eine Summe von komponentenweisen Produkten aus 2 oder mehreren Matrizen (siehe Summenprodukt).

Beispiel Tabellenkalkulation

Wir simulieren in dieser Tabelle einen Diffusionsprozess auf einer zweidimensionale Fläche. Diese wird mit Hilfe einer 5x6-Matrix dargestellt. In diese wird zunächst das anfängliche Schadstoffvorkommen eingetragen. Im Anschluss wird festgelegt, wie die Schadstoffe sich von einer Zelle in die benachbarten Zellen verteilen. Dafür wird eine 3x3-Matrix erstellt.

Verteilung der Schadstoffe auf eine Nachbarschaft

In Abhängigkeit von der Nachbarschaftsfestlegung werden die Schadstoffe in der zentralen Zelle anteilig im nächsten Zeitschritt $t+1$ auf die Zelle selbst und die Nachzelle verteilt. Wir betrachten zunächst zwei grundlegende Nachbarschaftsdefinitionen:

In diesem Beispiel wird die Moore-Nachbarschaft für die Zellbezüge verwendet.

Startkonfiguration zum Zeitpunkt t=0

Eine Tabellenkalkulationsdatei kann mehrere Tabellen enthalten. Die erste Tabelle zeigt die Startkonfiguration zum Zeitpunkt $t=0$ . Die folgende Interationsschritte werden in der nächsten Tabelle dargestellt.

Statische Objekte im Raum

Statische Objekte im Raum stellen Hindernisse für die Ausbreitung dar. Diese werden in einer separaten Tabelle gespeichert. Die statischen Hindernisse werden bei Umgebung berücksichtigt und legen damit fest, in welche Richtung sich ein Stoff nicht ausbreiten kann.

Dynamische Objekte im Raum

Im Gegensatz zu statischen Objekte im Raum stellen bewegliche Objekte ebenfalls Hindernisse für den Diffusionprozes dar. Diese müssen dann allerding in einer separaten Tabelle gespeichert. Für dynamische Hindernisse muss man dann allerdings für jeden Zeitpunkt $t$ ein eigenes Tabellenblatt anlegen werden bei Umgebung berücksichtigt und legen. Einerseits müssen dynamische Objekte (wie z.B. Fahrzeuge) feststehende Hindernisse berücksichtigen und andererseits sind die Hindernisse für die Diffusion die Zusammenfassung von dynamischen und statischen Hindernissen, die Diffusion in bestimmte Richtung einschränken.

Aufgaben

Wie kann man die Bewegung eines Fahrzeugs auf einer Kreisbahn modellieren?
Wie kann man einem digitalen Fahrzeug^[1] ein Ziel angeben, wober das Fahrzeug selbst einen Weg an den Hindernissen vorbei finden muss?

Quellennachweise

↑ Rauch, S., Aeberhard, M., Ardelt, M., & Kämpchen, N. (2012). Autonomes Fahren auf der Autobahn–eine Potentialstudie für zukünftige Fahrerassistenzsysteme. In 5. Tagung Fahrerassistenz.

Siehe auch

[1] Rauch, S., Aeberhard, M., Ardelt, M., & Kämpchen, N. (2012). Autonomes Fahren auf der Autobahn–eine Potentialstudie für zukünftige Fahrerassistenzsysteme. In 5. Tagung Fahrerassistenz.

[1]