Diffusion

Diffusion (lat. diffundere ‚ausgießen‘, ‚verstreuen‘, ‚ausbreiten‘) ist der ohne äußere Einwirkung eintretende Ausgleich von Konzentrationsunterschieden als natürlich ablaufender physikalischer Prozess aufgrund der brownschen Molekularbewegung. Er führt mit der Zeit zur vollständigen Durchmischung zweier oder mehrerer Stoffe durch die gleichmäßige Verteilung der beweglichen Teilchen und erhöht damit die Entropie des Systems. Bei den Teilchen kann es sich um Atome, Moleküle, Ladungsträger oder auch um freie Neutronen handeln. Meist ist zumindest einer der Stoffe ein Gas oder eine Flüssigkeit, doch können auch Feststoffe und Plasmen ineinander diffundieren.

Diffusion - Blauer Farbtropfen in Wasser

Farbunterschiede kodieren Konzentrationsunterschiede. Diffusion gleicht die Konzentrationsunterschiede im zeitlichen Verlauf aus - weitere Animationen.

Modellhafte Darstellung der Durchmischung zweier Stoffe durch Diffusion

Animation zur Schadstoffverteilung von 2 stehenden und 2 sich bewegenden Pkw - Anna Hundertmark 2019

Video wurde am Rhein in Köln/Rodenkirchen aufgenommen und es zeigt den Einfluss von Schiffen auf den Wasserstand (2018).

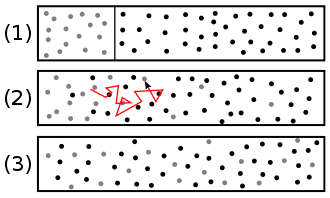
In dieser Lerneinheit wird die Ausbreitung von Stoffen in einer Umgebung allerdings nicht allein aus physikalischer Sicht behandelt, sondern auch die

• Ausbreitung von Informationen in Netzwerken,
• Ausbreitung von Risiken,
• ...

Die Diskretisierung der Umgebung kann z.B. zur eine Einführung von Graphen führen, über die sich die Stoffe ausbreiten. Die Diskretisierung ist in dieser Lerneinheit wesentlich, um Modellierungsergebnisse zu veranschaulichen und im Kontext eines Modellbildungszyklus auch zu validieren.

Lerneinheiten

Hinweise zur Prüfung

• Gemeinsamkeiten und Unterschiede

Einführung und Visuelle Darstellung

• Allgemeine Hinweise
• Animationen - visuelle Analyse der Diffusion
• Einführung in die Diffusion
• Geschichte und Theorieentwicklung der Diffusion
• Praktische Beispiele
• Hydrologie und Wasserverdrängung durch ein Schiff

Mathematische/Physikalische Grundlagen

• Kurs:Mathematische Modellbildung
• Physikalische Grundlagen
• Einführung in die Diffusion
• Räumliche Diffusion - Differentialgleichungen
• Verteilungen für Zellen

Implentation/Softwareeinsatz

• Tabellenkalkulation
• Octave-Tutorial für die 3D-Diffusion

Fächerübergreifende Aspekte

• Müllentsorgung in Netzwerken
• Epidemiologie - Masernverbreitung in Deutschland
• Risikomanagement
• Schnittstellenanalyse
• CO-Ausstoß in Landau
• Flüchtlingsströme im Schengen Raum
• Kreisverkehr vs Kreuzung
• Sport und Schadstoffexposition
• Grenzen des Wachstums

Animation zur Schadstoffverteilung

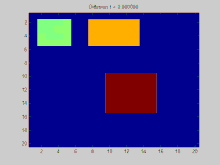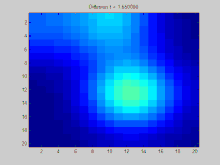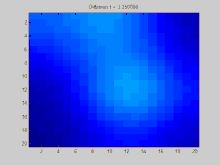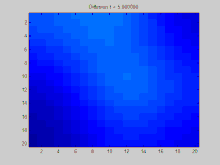
In dieser Lerneinheit wird die Verteilung von Schadstoffen als Thema behandelt. Ausgangspunktpunkt ist eine Animation (Hundermark 2019), die die Schadstoffemission von 2 stehenden Pkw und 2 sich bewegenden Pkw darstellt. In der Lerneinheiten werden die innermathematischen Aspekte und fächerübergreifende Lerninhalte behandelt, die mit Schadstoffemissionen in Zusammenhang stehen (siehe auch Räumliche Diffusion).

Animation zur Schadstoffausbreitung (A. Hundertmark 2019)

Blau gekennzeichnet ist der Bereich direkt hinter dem Auspuff, da dort bei der Emission die höchste Konzentration von Schadstoffen vorliegt. Auf der rechten Seiten finden Sie eine Skala, die Schadstoffexposition in der Ebene farblich kodiert.

Aufgaben

• (Systemisches Denken) Diffusion beschreibt zunächst einmal einen Verteilungsprozes auf mathematische Weise. Integriert man die Mathematik in einen konkreten Anwendungskontext, z.B. die Exposition mit Schadstoffe, sind neben der Mathematik schnell andere Disziplinen (Technik, Medizin, Umweltwissenschaften, Biologie, Toxikologie, Chemie, ...). Versuchen Sie für sich eine Mindmap zu erstellen, die alle Bereiche enthält, die aus Ihrer Sicht mit dem Thema "Exposition mit Schadstoffe" verbunden. Ergänzen Sie ggf. auch die tabellarische Ausstellung zur Schnittstellenanalyse.
• (Osmose und Diffusion) Analysieren die Prozesse bei der Osmose mit einer semipermeablen Membran. Wo liegen Gemeinsamkeiten und Unterschiede zur Diffusion im Kontext der Schadstoffverteilung?
• (Tabellenkalkulation) Erstellen Sie ein Tabellenkalkulationsblatt, bei dem jeweils eine Tabelle in einem Gitter die Schadstoffverteilung repräsentiert und die Verteilung der Schadstoffe.
• (Diffusion/Epdidemiologische Ausbreitung) Vergleichen Sie die Diffusion von Schadstoffen im Raum mit der Verbreitung von Viren. Welche Gemeinsamkeiten und Unterschiede können Sie entdecken. Häuser und andere Objekte im Raum bilden Barrieren für den Diffusionsprozess von Schadstoffen. Welche Barrieren gibt es für die epidemiologische Ausbreitung (z.B. Impfungen, Desinfektion, Einschränkung der Mobilität, ...), um die Ausbreitung zu verlangsamen? Welche Analogie können Sie bei der Ausbreitung von Schadsftoffen entdecken?

Falsche Wortanwendung von Diffusion

Die Begriffe Diffusion und Diffusivität werden auf dem Gebiet der Akustik häufig statt des deutschen Wortes Diffusität verwendet. Die falsche Übersetzung aus dem Englischen trägt dazu bei.

Siehe auch

• 2D-Animation
• Projektarbeit in Wikiversity
• Räumliche Diffusion
• Reaktions-Diffusionsgleichung
• Eddy-Diffusion, bezeichnet Vermischung durch Strömung
• Knudsen-Diffusion, durch Begrenzungen dominierte Diffusion
• Kritische Schichtdicke
• Lévy-Prozess
• Diffusionsnetz
• Diffusionsstrom
• Diffusivität
• Neutronendiffusion
• Kategorie:Statistische Physik
• Kategorie:Physikalische Chemie
• Wikipedia-Artikel mit Video
• Systemisches Denken
• Wasser
• Dieselaffäre und Dieselruß
• Photogrammetry/Regard3D mit einer Standardkamera ein 3D-Modell einer Verkehrskreuzung mit Gebäuden erstellen.

Literatur

• Peter W. Atkins, Charles A. Trapp: Physikalische Chemie. 3. korrigierte Auflage. Wiley-VCH, Weinheim u. a. 2001, lSBN 3-527-30236-0.
• E. L. Cussler: Diffusion. Mass Transfer in Fluid Systems. 2nd edition. Cambridge University Press, Cambridge u. a. 1997, lSBN 0-521-56477-8.
• J. Crank: The Mathematics of Diffusion. 2nd revised edition. Oxford University Press, Oxford u. a. 1980, lSBN 0-19-853411-6.
• Paul Heitjans, Jörg Kärger (Hrsg.): Diffusion in Condensed Matter. Methods, Materials, Models. Greatly enlarged and completely revised edition. Springer, Berlin u. a. 2005, lSBN 3-540-20043-6.
• Jörg Kärger (Hrsg.): Leipzig, Einstein, Diffusion. Leipziger Universitätsverlag, Leipzig, 2007, (3. Auflage 2014), lSBN 978-3-86583-176-7
• Wilhelm Jost: Diffusion in solids, liquids, gases (= Physical chemistry 1, ISSN 0079-1881). 6th printing. Academic Press, New York NY 1970.
• H. J. V. Tyrrell, K. R. Harris: Diffusion in Liquids. A theoretical and experimental Study. Butterworth, London 1984, lSBN 0-408-17591-5.

Weblinks

Wiktionary

 Wiktionary: Diffusion – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Commons: Diffusion – Sammlung von Bildern, Videos und Audiodateien

• Die Fickschen Diffusionsgesetze, H. Föll, Technische Fakultät der Christian-Albrechts-Universität zu Kiel
• Diffusion in Physikalische Werkstoffeigenschaften (PDF-Datei, 160 kB) beim Leibniz-Institut für Festkörper- und Werkstoffforschung
• 3D-Gitter-Monte-Carlo-Simulation der Diffusion auf einer vizinal geschnittenen kfz-(100)-Oberfläche von Lars Röntzsch
• NetLogo-Simulationsmodell für den Unterricht (Java-Applet) von Johannes Kottonau
• Diffussion und Ficksche Gesetze – wie schnell geht Stofftransport ohne Strömung? Herausgeber: Lauth (2013) DOI=10.5446/15654

Seiten-Information

Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:

• Diffusion https://de.wikipedia.org/wiki/Diffusion
• Datum: 12.4.2019
• Wikipedia2Wikiversity-Konverter: https://niebert.github.com/Wikipedia2Wikiversity