Es sei  die Menge der natürlichen Zahlen und
die Menge der natürlichen Zahlen und
 die
Produktmenge
mit der komponentenweisen Addition. Wir erklären auf
die
Produktmenge
mit der komponentenweisen Addition. Wir erklären auf  eine
Relation
durch
eine
Relation
durch
-

Es wird hier also über Kreuz addiert, um diese Relation zu erhalten. Diese Relation ist bei
 genau dann erfüllt, wenn es ein
genau dann erfüllt, wenn es ein  (nämlich die natürliche Zahl
(nämlich die natürliche Zahl  )
mit
)
mit
-

gibt und bei
 genau dann erfüllt, wenn es ein
genau dann erfüllt, wenn es ein
 (nämlich
(nämlich
 )
mit
)
mit
-

gibt. So oder so kann man sagen, dass die Paare
 und
und  zueinander äquivalent sind, wenn sie sich um ein Diagonalelement, also um ein Paar, wo beide Komponenten übereinstimmen, unterscheiden. Diese Relation ist eine Äquivalenzrelation auf
zueinander äquivalent sind, wenn sie sich um ein Diagonalelement, also um ein Paar, wo beide Komponenten übereinstimmen, unterscheiden. Diese Relation ist eine Äquivalenzrelation auf  . Das ist von der soeben etablierten Interpretation als „gleichdiagonalig“ her klar, kann aber auch direkt gezeigt werden:
. Das ist von der soeben etablierten Interpretation als „gleichdiagonalig“ her klar, kann aber auch direkt gezeigt werden:
- Wegen
 ist
ist
 ,
die Relation ist also reflexiv.
,
die Relation ist also reflexiv.
- Die Symmetrie folgt daraus, dass aus
 sofort
sofort
 folgt.
folgt.
- Zum Nachweis der Transitivität sei
 und
und  ,
also
,
also
 und
und
 .
Dann ist
.
Dann ist
-

Aufgrund
der Abziehregel
ist dann
-

und dies bedeutet
 .
.
Passende Interpretationen für die Paare mit dieser Äquivalenzrelation sind beispielsweise:
- Das Paar
 repräsentiert das Ergebnis eines Fußballspieles, wobei
repräsentiert das Ergebnis eines Fußballspieles, wobei  die Toranzahl der Heimmannschaft und
die Toranzahl der Heimmannschaft und  die Toranzahl der Gastmannschaft repräsentiert. Zwei Spiele gelten dann als äquivalent, wenn die „gerichtete Differenz“ gleich ist. Ein
die Toranzahl der Gastmannschaft repräsentiert. Zwei Spiele gelten dann als äquivalent, wenn die „gerichtete Differenz“ gleich ist. Ein  wird als äquivalent zu einem
wird als äquivalent zu einem  betrachtet, wenn beide Mannschaften ein weiteres Tor schießen, ändert sich zwar das Paar, aber nicht die Äquivalenzklasse. Die Äquivalenzklassen kann man charakterisieren als Unentschieden, mit einem Tor Vorsprung gewonnen, mit zwei Toren Vorsprung gewonnen, mit drei Toren Vorsprung gewonnen, ... , mit einem Tor Unterschied verloren, mit zwei Toren Unterschied verloren, mit drei Toren Unterschied verloren, ....
betrachtet, wenn beide Mannschaften ein weiteres Tor schießen, ändert sich zwar das Paar, aber nicht die Äquivalenzklasse. Die Äquivalenzklassen kann man charakterisieren als Unentschieden, mit einem Tor Vorsprung gewonnen, mit zwei Toren Vorsprung gewonnen, mit drei Toren Vorsprung gewonnen, ... , mit einem Tor Unterschied verloren, mit zwei Toren Unterschied verloren, mit drei Toren Unterschied verloren, ....
- Das Paar
 repräsentiert das Alter eines menschlichen Paares, wobei
repräsentiert das Alter eines menschlichen Paares, wobei  für das Alter der Frau und
für das Alter der Frau und  für das Alter des Mannes steht. Die Äquivalenzklasse ist durch den gerichteten Altersunterschied (also den Altersunterschied mit der zusätzlichen Information, wer älter ist)
für das Alter des Mannes steht. Die Äquivalenzklasse ist durch den gerichteten Altersunterschied (also den Altersunterschied mit der zusätzlichen Information, wer älter ist)
festgelegt. Diese Beziehung ändert sich im Laufe des Lebens nicht, da beide gleichermaßen älter werden.
- Das Paar
 kann die Einnahmen und Ausgaben eines Haushaltes in einem Monat beschreiben, wobei die erste Stelle die Einnahmen und die zweite Stelle die Ausgaben repräsentieren möge. Zwei Haushalte
kann die Einnahmen und Ausgaben eines Haushaltes in einem Monat beschreiben, wobei die erste Stelle die Einnahmen und die zweite Stelle die Ausgaben repräsentieren möge. Zwei Haushalte
(oder Monate)
sind dann äquivalent, wenn sie den gleichen Überschuss oder das gleiche Defizit erwirtschaftet haben. Wenn Einnahmen und Ausgaben gleichermaßen steigen oder fallen, ändert sich an dieser Gesamtbewertung nichts.
- Man kann das Paar als eine Schrittfolge aus
 Schritten nach rechts und
Schritten nach rechts und  Schritten nach links ansehen. Im Paar selbst wird die Anzahl der Schritte in die beiden Richtungen notiert, für die Äquivalenzrelation schaut man nur das Endergebnis des Bewegungsvorganges an.
Schritten nach links ansehen. Im Paar selbst wird die Anzahl der Schritte in die beiden Richtungen notiert, für die Äquivalenzrelation schaut man nur das Endergebnis des Bewegungsvorganges an.
Wenn man  als ein quadratisches Gitter anordnet
(das ist ein „diskretes Koordinatensystem“),
so sind die Äquivalenzklassen durch die Punkte auf einer zur Diagonalen parallelen „diskreten Geraden“ gegeben. Die Punkte
als ein quadratisches Gitter anordnet
(das ist ein „diskretes Koordinatensystem“),
so sind die Äquivalenzklassen durch die Punkte auf einer zur Diagonalen parallelen „diskreten Geraden“ gegeben. Die Punkte  mit
mit
 sind äquivalent zu
sind äquivalent zu  , sie haben also einen Repräsentanten, bei dem die zweite Komponente
, sie haben also einen Repräsentanten, bei dem die zweite Komponente  ist. Die Punkte
ist. Die Punkte  mit
mit
 sind äquivalent zu
sind äquivalent zu  , sie haben also einen Repräsentanten, bei dem die erste Komponente
, sie haben also einen Repräsentanten, bei dem die erste Komponente  ist. Die Punkte
ist. Die Punkte  sind zu
sind zu  äquivalent. Den Repräsentanten einer Äquivalenzklasse, bei dem mindestens eine Komponente
äquivalent. Den Repräsentanten einer Äquivalenzklasse, bei dem mindestens eine Komponente  ist, nennen wir den Standardvertreter dieser Äquivalenzklasse. Die Standardvertreter sind die diskreten Punkte des begrenzenden Viertelkreuzes; zu einem Punkt ergibt sich der Standardvertreter, indem man parallel zur Diagonalen in Richtung der Halbachsen wandert, bis man auf einer der Halbachsen landet. Zwei Punkte sind genau dann äquivalent, wenn sie den gleichen Standardvertreter besitzen.
ist, nennen wir den Standardvertreter dieser Äquivalenzklasse. Die Standardvertreter sind die diskreten Punkte des begrenzenden Viertelkreuzes; zu einem Punkt ergibt sich der Standardvertreter, indem man parallel zur Diagonalen in Richtung der Halbachsen wandert, bis man auf einer der Halbachsen landet. Zwei Punkte sind genau dann äquivalent, wenn sie den gleichen Standardvertreter besitzen.
Wir bezeichnen nun die
Quotientenmenge,
also die Menge der Äquivalenzklassen unter dieser Äquivalenzrelation, als Menge der ganzen Zahlen und bezeichnen sie mit  . Wir sprechen vom Äquivalenzklassenmodell oder Paarmodell für die ganzen Zahlen. Diese Quotientenmenge ist die Menge der zur Diagonalen parallelen diskreten Geraden, bei der kanonischen Projektion wird jedes Paar
. Wir sprechen vom Äquivalenzklassenmodell oder Paarmodell für die ganzen Zahlen. Diese Quotientenmenge ist die Menge der zur Diagonalen parallelen diskreten Geraden, bei der kanonischen Projektion wird jedes Paar  auf die Gerade abgebildet, auf der es liegt. Jede ganze Zahl hat genau einen Standardvertreter der Form
auf die Gerade abgebildet, auf der es liegt. Jede ganze Zahl hat genau einen Standardvertreter der Form
 mit
mit  , der Form
, der Form
 oder der Form
oder der Form
 mit
mit  . Eine natürliche Zahl
. Eine natürliche Zahl  fassen wir in diesem Modell als die ganze Zahl
fassen wir in diesem Modell als die ganze Zahl  auf, und negative Zahlen werden als spezielle Äquivalenzklassen eingeführt.
auf, und negative Zahlen werden als spezielle Äquivalenzklassen eingeführt.
Wir wollen nun zwei ganze Zahlen, also zwei solche Äquivalenzklassen
![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a) und
und ![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1) ,
miteinander „addieren“, also eine Verknüpfung
,
miteinander „addieren“, also eine Verknüpfung  auf
auf  einführen. Ein Ansatz, der sich durch den Zugang über Äquivalenzklassen eröffnet, ist es, auf der Menge der Paare die Addition zu nehmen und zu versuchen, diese Addition auf die Äquivalenzklassen zu übertragen. Die komponentenweise Addition auf
einführen. Ein Ansatz, der sich durch den Zugang über Äquivalenzklassen eröffnet, ist es, auf der Menge der Paare die Addition zu nehmen und zu versuchen, diese Addition auf die Äquivalenzklassen zu übertragen. Die komponentenweise Addition auf  , also die Verknüpfung
, also die Verknüpfung
-

ist recht einfach und insbesondere ist diese Verknüpfung kommutativ, assoziativ und  ist das neutrale Element. Diese Addition hat in den oben angegebenen Beispielen eine sinnvolle Interpretation, wie wenn man die Ergebnisse von zwei Fußballspielen miteinander addiert
(Hin- und Rückspiel, allerdings muss man die Reihenfolge beibehalten)
oder das Haushaltsgeschehen von mehreren Monaten addiert.
ist das neutrale Element. Diese Addition hat in den oben angegebenen Beispielen eine sinnvolle Interpretation, wie wenn man die Ergebnisse von zwei Fußballspielen miteinander addiert
(Hin- und Rückspiel, allerdings muss man die Reihenfolge beibehalten)
oder das Haushaltsgeschehen von mehreren Monaten addiert.
Durch die Festlegung
-
![{\displaystyle {}[(a,b)]+[(c,d)]:=[(a+c,b+d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df3c8ae9fedcdfe86d6be396243b2aaa93a5465d)
erhält man auf
(dem Äquivalenzklassenmodell von)
 eine Verknüpfung, die kommutativ und assoziativ ist und die
eine Verknüpfung, die kommutativ und assoziativ ist und die ![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9) als neutrales Element besitzt. Darüber hinaus besitzt jedes Element ein inverses Element, und zwar sind
als neutrales Element besitzt. Darüber hinaus besitzt jedes Element ein inverses Element, und zwar sind
![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a) und
und ![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8) invers zueinander.
invers zueinander.
Wir müssen zuerst die Wohldefiniertheit überprüfen, da die Verknüpfung unter Bezug auf Repräsentanten erklärt wird und daher nicht von vornherein klar ist, dass unterschiedliche Repräsentanten zum gleichen Ergebnis
(zur gleichen Äquivalenzklasse)
führen. Zu
 und
und
 muss man überprüfen, dass
muss man überprüfen, dass
-

und damit
![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb) gilt. Die beiden Voraussetzungen bedeuten ausgeschrieben
gilt. Die beiden Voraussetzungen bedeuten ausgeschrieben
 und
und
 .
Damit ist durch Addition der beiden Gleichungen
.
Damit ist durch Addition der beiden Gleichungen
-

was die Äquivalenz bedeutet. Die kanonische Abbildung
-
![{\displaystyle q\colon \mathbb {N} \times \mathbb {N} \longrightarrow \mathbb {Z} ,\,(a,b)\longmapsto [(a,b)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d579ea0ed3a15555fc962cce8c7abecb628a9577)
verträgt sich nach Konstruktion mit der Addition auf der Produktmenge und der soeben etablierten Addition auf  , es ist also
, es ist also
-

für alle  . In einer solchen Situation übertragen sich wegen der Surjektivität der kanonischen Abbildung Rechengesetze von
. In einer solchen Situation übertragen sich wegen der Surjektivität der kanonischen Abbildung Rechengesetze von  direkt auf die Quotientenmenge. Für das Assoziativgesetz beispielsweise betrachten wir Elemente
direkt auf die Quotientenmenge. Für das Assoziativgesetz beispielsweise betrachten wir Elemente  . Es gibt
. Es gibt  mit
mit
 ,
,
 ,
,
 .
Somit ist
.
Somit ist

Der Nachweis der Kommutativität und dass ![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9) das
neutrale Element
der Verknüpfung ist, verläuft ähnlich einfach. Wegen
das
neutrale Element
der Verknüpfung ist, verläuft ähnlich einfach. Wegen
-
![{\displaystyle {}[(a,b)]+[(b,a)]=[(a+b,a+b)]=[(0,0)]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30f5374e76e9009d2e2dbd60105b4efe5b036407)
ist in der Tat ![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8) das inverse Element zu
das inverse Element zu ![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a) .
.

Durch die Festlegung
-
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/271e150f46d092c8a4e0ae63c57aeb711ce6f96d)
erhält man auf
(dem
Äquivalenzklassenmodell
von)
 eine
Verknüpfung,
die
kommutativ
und
assoziativ
ist und die
eine
Verknüpfung,
die
kommutativ
und
assoziativ
ist und die ![{\displaystyle {}[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/729d0600c281952f3efa4039a3bab1a6d0c9833c) als
neutrales Element
besitzt.
als
neutrales Element
besitzt.
Beweis
Siehe
Aufgabe.

Das Äquivalenzklassenmodell von  ist mit der Addition
ist mit der Addition
-
![{\displaystyle {}[(a,b)]+[(c,d)]:=[(a+c,b+d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26a52d48bd8d6752f000b989c01ac00bcf01a57c)
der Multiplikation
-
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b51e69acf3691a66a51c3e1ceab6b3409966341)
dem Nullelement ![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9) und dem Einselement
und dem Einselement ![{\displaystyle {}[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/729d0600c281952f3efa4039a3bab1a6d0c9833c)
ein
kommutativer Ring.
Aufgrund von
Fakt
und
Fakt
müssen wir nur noch das Distributivgesetz überprüfen. Dieses ist wegen
![{\displaystyle {}{\begin{aligned}\,[(a,b)]{\left([(c,d)]+[(e,f)]\right)}&=[(a,b)][(c+e,d+f)]\\&=[(ac+ae+bd+bf,ad+af+bc+be)]\\&=[(ac+bd,ad+bc)]+[(ae+bf,af+be)]\\&=[(a,b)][(c,d)]+[(a,b)][(e,f)]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67e7270a328cd2dd219470b02b9b5b37d5c40df3)
erfüllt.

Durch die Festlegung
-
![{\displaystyle {}[(a,b)]\geq [(c,d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2391d3d11caaf252146ce25295282921cd03a980)
falls
-

erhält man auf
(dem Äquivalenzklassenmodell von)
 eine
totale Ordnung.
eine
totale Ordnung.
Beweis
Siehe
Aufgabe.

Das Äquivalenzklassenmodell von  ist mit der Addition
ist mit der Addition
-
![{\displaystyle {}[(a,b)]+[(c,d)]:=[(a+c,b+d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26a52d48bd8d6752f000b989c01ac00bcf01a57c)
der Multiplikation
-
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b51e69acf3691a66a51c3e1ceab6b3409966341)
dem Nullelement ![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9) , dem Einselement
, dem Einselement ![{\displaystyle {}[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/729d0600c281952f3efa4039a3bab1a6d0c9833c) und der durch
und der durch
-
![{\displaystyle {}[(a,b)]\geq [(c,d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2391d3d11caaf252146ce25295282921cd03a980)
falls
-

definierten Ordnung
ein
angeordneter Ring.
Nach
Fakt
ist  ein kommutativer Ring und nach
Fakt
ist
ein kommutativer Ring und nach
Fakt
ist  eine totale Ordnung. Wir müssen also lediglich noch die Verträglichkeit der Ordnung mit der Addition und der Multiplikation überprüfen. Sei
eine totale Ordnung. Wir müssen also lediglich noch die Verträglichkeit der Ordnung mit der Addition und der Multiplikation überprüfen. Sei
-
![{\displaystyle {}[(a,b)]\geq [(c,d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2391d3d11caaf252146ce25295282921cd03a980)
also
 ,
und
,
und ![{\displaystyle {}[(e,f)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/950de1f8b81cd13973e091bc0624d31c8b02ec5b) beliebig. Dann ist auch
beliebig. Dann ist auch
-

also
-
![{\displaystyle {}[(a,b)]+[(e,f)]=[(a+e,b+f)]\geq [(c+e,d+f)]=[(c,d)]+[(e,f)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb89e90d55c6ffb32049a8b7957801613ade863)
Wenn
![{\displaystyle {}[(a,b)]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a6b964ca907a4cac05f73b2f3c514df5e6621f) und
und
![{\displaystyle {}[(c,d)]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f31586de78745b4a1bd461ab37f6fe9e1100600) ist, so ist
ist, so ist
 und
und
 .
Mit
Aufgabe
ergibt sich
.
Mit
Aufgabe
ergibt sich
-

was
-
![{\displaystyle {}[(a,b)]\cdot [(c,d)]=[(ac+bd,ad+bc)]\geq 0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e24997a1efecaea2c8d611c80994c486c8d0a8df)
bedeutet.

Die natürlichen Zahlen  sind über die Zuordnung
sind über die Zuordnung
-
![{\displaystyle \mathbb {N} \longrightarrow \mathbb {Z} ,\,n\longmapsto [(n,0)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df42efcb5d068e5db603918e70ac6e888c3dc981)
in den ganzen Zahlen enthalten. Diese Zuordnung ist mit der Addition, der Multiplikation und der Ordnung verträglich, siehe
Aufgabe.
Statt  schreibt man einfach
schreibt man einfach  . Die ganzen Zahlen, die durch
. Die ganzen Zahlen, die durch  mit
mit  repräsentiert werden, heißen negative Zahlen. Statt
repräsentiert werden, heißen negative Zahlen. Statt  schreibt man einfach
schreibt man einfach  .
.



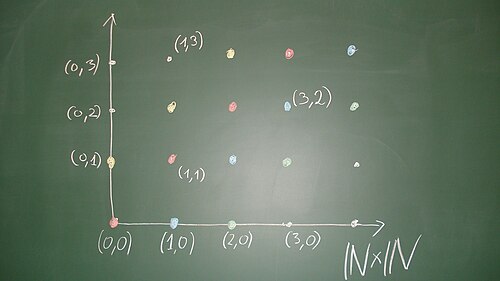







































![{\displaystyle {}[(a,b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad856e5411d0b9ea10ddb04a48932aef19892e7a)
![{\displaystyle {}[(c,d)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b865712c6f9654641f6315839d7fb250d5ed6fa1)



![{\displaystyle {}[(a,b)]+[(c,d)]:=[(a+c,b+d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df3c8ae9fedcdfe86d6be396243b2aaa93a5465d)
![{\displaystyle {}[(0,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/475a6889495e16a90a7bddd389ad803ee5e078f9)
![{\displaystyle {}[(b,a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7257885d4524a38fea17a5ad720d33f256cdeaf8)



![{\displaystyle {}[(a+c,b+d)]=[(a'+c',b'+d')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b9bc368eabf53b7c89081c97a70ea09b665f4fb)



![{\displaystyle q\colon \mathbb {N} \times \mathbb {N} \longrightarrow \mathbb {Z} ,\,(a,b)\longmapsto [(a,b)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d579ea0ed3a15555fc962cce8c7abecb628a9577)








![{\displaystyle {}[(a,b)]+[(b,a)]=[(a+b,a+b)]=[(0,0)]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30f5374e76e9009d2e2dbd60105b4efe5b036407)

![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/271e150f46d092c8a4e0ae63c57aeb711ce6f96d)
![{\displaystyle {}[(1,0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/729d0600c281952f3efa4039a3bab1a6d0c9833c)
![{\displaystyle {}[(a,b)]+[(c,d)]:=[(a+c,b+d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26a52d48bd8d6752f000b989c01ac00bcf01a57c)
![{\displaystyle {}[(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b51e69acf3691a66a51c3e1ceab6b3409966341)
![{\displaystyle {}{\begin{aligned}\,[(a,b)]{\left([(c,d)]+[(e,f)]\right)}&=[(a,b)][(c+e,d+f)]\\&=[(ac+ae+bd+bf,ad+af+bc+be)]\\&=[(ac+bd,ad+bc)]+[(ae+bf,af+be)]\\&=[(a,b)][(c,d)]+[(a,b)][(e,f)]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67e7270a328cd2dd219470b02b9b5b37d5c40df3)
![{\displaystyle {}[(a,b)]\geq [(c,d)]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2391d3d11caaf252146ce25295282921cd03a980)



![{\displaystyle {}[(e,f)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/950de1f8b81cd13973e091bc0624d31c8b02ec5b)

![{\displaystyle {}[(a,b)]+[(e,f)]=[(a+e,b+f)]\geq [(c+e,d+f)]=[(c,d)]+[(e,f)]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb89e90d55c6ffb32049a8b7957801613ade863)
![{\displaystyle {}[(a,b)]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a6b964ca907a4cac05f73b2f3c514df5e6621f)
![{\displaystyle {}[(c,d)]\geq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f31586de78745b4a1bd461ab37f6fe9e1100600)


![{\displaystyle {}[(a,b)]\cdot [(c,d)]=[(ac+bd,ad+bc)]\geq 0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e24997a1efecaea2c8d611c80994c486c8d0a8df)
![{\displaystyle \mathbb {N} \longrightarrow \mathbb {Z} ,\,n\longmapsto [(n,0)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df42efcb5d068e5db603918e70ac6e888c3dc981)

