Kurs:Diskrete Mathematik (Osnabrück 2020)/Arbeitsblatt 18

Übungsaufgaben

Aufgabe

Wir betrachten den Spielzuggraphen ${}G$ zum Turm auf einem ${}3\times 3$-Schachbrett.

1. Bestimme die Anzahl der linearen Spannbäume von ${}G$.
2. Bestimme die Anzahl der Spannbäume von ${}G$.

Aufgabe

Wir betrachten den Spielzuggraphen ${}G$ zum Läufer auf einem ${}4\times 4$-Schachbrett.

1. Bestimme die Anzahl der linearen Spannbäume von ${}G$.
2. Bestimme die Anzahl der Spannbäume von ${}G$.

Aufgabe

Es sei ${}F$ ein Rundgang mit ${}m$ Knoten und ${}H$ ein Rundgang mit ${}n$ Knoten, ${}m,n\geq 3$. Es sei ${}G$ die Vereinigung der beiden Graphen an einem einzigen Punkt. Zeige, dass die Anzahl der aufspannenden Bäume von ${}G$ gleich ${}mn$ ist.

Aufgabe

Es sei ${}G$ ein zusammenhängender Graph mit Durchmesser ${}d$. Zeige, dass es in ${}G$ einen aufspannenden Baum mit Durchmesser ${}d$ gibt.

Aufgabe

Es sei ${}G$ der vollständige Graph mit ${}n$ Knoten. Bestimme die Anzahl der linearen aufspannenden Bäume in ${}G$.

Kommentar:

Ein linearer aufspannender Baum ist einfach ein Untergraph von ${}G$, der ein Pfad ist. Er muss alle Punkte genau einmal enthalten, es handelt sich also um ein vollständiges und eindeutiges Durchlaufen des Graphen. Da es keine Wiederholungen der Knoten geben darf, gibt es erst recht keine Wiederholungen von Kanten (es gibt auch das Konzept Eulerzug, das wir später behandeln werden).

Bei einen vollständigen Graphen kann man an einem beliebigen Punkt anfangen, und dann zu einem beliebigen Punkt mittels der Kante laufen, dann ...

 

Aufgabe

Zeige, dass die Potenzmenge ${}{\mathfrak {P}}\,(E)$ zu einer Menge ${}E$ ein Matroid ist.

Aufgabe

Es sei ${}E$ eine Menge und ${}r\in \mathbb {N}$. Es sei ${}{\mathcal {M}}$ die Menge aller Teilmengen von ${}E$, die höchstens ${}r$ Elemente enthalten. Zeige, dass ${}{\mathcal {M}}$ ein Matroid ist.

Aufgabe

Es sei ${}E$ die Familie der folgenden Vektoren im ${}\mathbb {R} ^{2}$.

$(0,0),\,(4,0),\,(2,3),\,(4,6),\,(5,7),\,(3,0),\,(0,3).$

Bestimme das Matroid, das durch die lineare Unabhängigkeit von Teilfamilien gegeben ist.

Aufgabe

Es sei ${}G$ ein zusammenhängender Graph. Zeige, dass für einen Untergraphen ${}H=(V,F)\subseteq G$ (also mit voller Vertexmenge) die folgenden Aussagen äquivalent sind.

1. ${}H$ ist ein Baum.
2. ${}H$ ist ein aufspannender Baum.
3. ${}H$ ist maximal kreisfrei, d. h. sobald man eine Kante aus ${}G$ zu ${}H$ hinzutut, entsteht ein Kreis.
4. ${}H$ ist minimal zusammenhängend, d. h. sobald man eine Kante herausnimmt, wird der Graph unzusammenhängend.

Kommentar:

Die Aussage sollte strukturell an die Aussage der linearen Algebra errinnern: Eine Familie von Vektoren ist genau dann eine Basis, wenn sie eine maximal linear unabhängig ist genau dann, wenn sie ein minimales Erzeugendensystem ist, siehe Satz 7.11 (Lineare Algebra (Osnabrück 2017-2018)). Die Analogie zwischen (aufspannenden) Bäumen bzw. Wälder zu (maximal) linear unabhängigen Vektorfamilien wird ja bereits durch den Matroidbegriff präzise gemacht. (1) und (2) sind trivialerweise äquivalent, da ja ein aufspannender Baum einfach ein Baum mit der vollen Knotenmenge ist, was vorausgesetzt wird. Von (2) nach (3). Es werde die Kante ${}\{u,v\}$ hinzugenommen. Es gibt aber bereits in ${}H$ einen verbindenden Weg von ${}u$ nach ${}v$ und durch die Hinzunahme entsteht ein mehrfacher Weg und ein Kreis. Dieses Argument wurde schon im Beweis zu Satz 17.22 verwendet.

Von (3) nach (1). Es ist zu zeigen, dass unter der angegebenen Bedingung ${}H$ zusammenhängend ist. Wenn ${}H$ nicht zusammenhängend ist, so gebe es keinen Weg in ${}H$ von ${}u$ nach ${}v$. Es gibt in ${}G$ nach der Obervoraussetzung einen Weg von ${}u$ nach ${}v$. Zumindest eine Kante davon gehört nicht zu ${}H$, nach Umbenennung sei das die Kante ${}\{u,v\}$. Wenn man aber diese Kante zu ${}H$ hinzunimmt, entsteht ein größerer kreisfreier Untergraph.

Von (1) nach (4) folgt aus Satz 17.22, wenn man die Kante ${}\{u,v\}$ herausnimmt, so zerstört man den eindeutigen wiederholungsfreien Verbindungsweg von ${}u$ nach ${}v$.

Von (4) nach (1) folgt ebenfalls aus Satz 17.22.

 

Aufgabe

Es sei ${}G$ ein Rundgang mit ${}n$ Knotenpunkten. Bestimme die Anzahl der Spannbäume von ${}G$ mit und ohne Lemma 18.12.

Aufgabe

Es sei ${}G$ ein Graph. Zeige mit und ohne Lemma 18.12, dass die Anzahl der Spannbäume von ${}G$ mit der Anzahl der Spannbäume des Graphen ${}H$ übereinstimmt, der aus ${}G$ entsteht, indem man alle Blätter zusammen mit den zugehörigen Kanten entfernt.

Kommentar:

Da man die Blätter sukzessive entfernen kann, muss man lediglich zeigen, dass die Anzahl der aufspannenden Bäume gleich bliebt, wenn man ein Blatt zusammen mit der anliegenden Kanten entfernt. Sei also ${}b$ ein Blatt mit zugehöriger Kante ${}e=\{b,u\}$.

Jeder aufspannende Baum muss das Blatt ${}b$ enthalten, und die einzige Möglichkeit ist über die einzige Kante ${}\{b,u\}$. Wenn man das Blatt und diese Kante entfernt, so erhält man nach Lemma 17.21 wieder einen (Spann)-Baum. Wenn umgekehrt ein aufspannender Baum von des reduzierten Graphen vorliegt, so wird dieser durch Hinzunahme des Blattes und der Kante zu einem Spannbaum des Ausgangsgraphen. Es gibt also eine natürliche Bijektion zwischen den aufspannenden Bäumen des Graphen mit oder ohne dem Blatt.

Mit Lemma 18.12 geht das Argument so: Der Graph ${}G\setminus \{e\}$ (also mit dem Knoten ${}b$, aber ohne die verbindende Kante) ist nicht zusammenhängend und hat daher keinen Spannbaum. Damit stimmt die Anzahl der Spannbäume von ${}G$ mit der Anzahl der Spannbäume von ${}G/e$ überein. Das Argument von oben ist aber andererseits auch der wesentliche Punkt im Beweis des Lemmas.

 

Aufgabe

Bestimme rekursiv die Anzahl der aufspannenden Bäume des abgebildeten Graphen.

Aufgabe

Bestimme die Anzahl der aufspannenden Bäume des dreidimensionalen Würfelgraphen.

Aufgaben zum Abgeben

Aufgabe (2 Punkte)

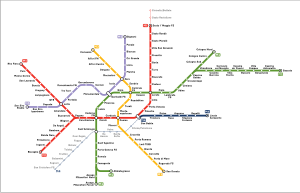
Man beschreibe einen Spannbaum für die Mailänder Metro, indem man gewisse Kanten herausnimmt.

Aufgabe (3 Punkte)

Auf der Knotenmenge ${}v_{1},\ldots ,v_{n}$ sei ein linearer Multigraph ${}G$ gegeben, wobei ${}a_{i}$, ${}i=1,\ldots ,n-1$, die Anzahl der Kanten zwischen ${}v_{i}$ und ${}v_{i+1}$ sei (und sonst gebe es keine Kanten). Zeige, dass die Anzahl der aufspannenden Bäume von ${}G$ gleich ${}a_{1}\cdots a_{n-1}$ ist.

Aufgabe (5 Punkte)

Bestimme rekursiv die Anzahl der aufspannenden Bäume des vollständigen Graphen mit ${}5$ Knotenpunkten.

Aufgabe (3 Punkte)

Bestimme rekursiv die Anzahl der aufspannenden Bäume des abgebildeten Graphen.

Aufgabe (5 Punkte)

Es sei ${}G$ ein Graph zusammen mit zwei vollen Untergraphen ${}F,H\subseteq G$ mit (auf der Vertexmenge)

${}F\cap H=\{P\}\,$

und derart, dass alle Kanten von ${}G$ entweder zu ${}F$ oder zu ${}H$ gehören. Zeige, dass die Anzahl der aufspannenden Bäume von ${}G$ gleich dem Produkt der Anzahl der aufspannenden Bäume von ${}F$ und der Anzahl der aufspannenden Bäume von ${}H$ ist.