Kurs:Analysis (Osnabrück 2021-2023)/Teil I/Vorlesung 4/kontrolle

„Wenn ich weiter geblickt habe, so deshalb, weil ich auf den Schultern von Riesen stehe“

Isaac Newton

Angeordnete Körper

Zwei reelle Zahlen kann man ihrer Größe nach vergleichen, d.h. die eine ist größer als die andere oder es handelt sich um die gleiche Zahl. Auf der Zahlengeraden bedeutet dies, dass die eine Zahl rechts von der anderen liegt. Die wesentlichen Eigenschaften der Größerbeziehung werden im Begriff des angeordneten Körpers zusammengefasst. Um dieses Konzept formulieren zu können, führen wir kurz die grundlegenden Begriffe Relation und Ordnungsrelation ein.

Definition Referenznummer erstellen

Es seien ${}X$ und ${}Y$ Mengen. Eine Relation zwischen ${}X$ und ${}Y$ ist eine Teilmenge ${}R\subseteq X\times Y$.

D.h. bei einer Relation stehen gewisse Paare ${}(x,y)$ in der gegebenen Relation, und die anderen Paare eben nicht. Man schreibt dafür ${}(x,y)\in R$ oder ${}R(x,y)$ oder ${}xRy$. Im Moment sind wir an Ordnungsrelationen interessiert, die folgendermaßen definiert werden.

Definition Referenznummer erstellen

Eine Relation ${}\preccurlyeq$ auf einer Menge ${}I$ heißt Ordnungsrelation oder Ordnung, wenn folgende drei Bedingungen erfüllt sind.

1. Es ist ${}i\preccurlyeq i$ für alle ${}i\in I$.
2. Aus ${}i\preccurlyeq j$ und ${}j\preccurlyeq k$ folgt stets ${}i\preccurlyeq k$.
3. Aus ${}i\preccurlyeq j$ und ${}j\preccurlyeq i$ folgt ${}i=j$.

Definition Referenznummer erstellen

Eine Ordnungsrelation ${}\preccurlyeq$ auf einer Menge ${}I$ heißt lineare Ordnung (oder totale Ordnung), wenn zu je zwei Elementen ${}x,y\in I$ die Beziehung ${}x\preccurlyeq y$ oder ${}y\preccurlyeq x$ gilt.

Wenn auf einer Menge ${}M$ eine totale Ordnung vorliegt, so bezeichnet man für zwei Elemente ${}x,y\in M$ das kleinere der beiden mit ${}{\min {\left(x,y\right)}}$ und das größere mit ${}{\max {\left(x,y\right)}}$. Man spricht vom Minimum und vom Maximum.

Definition Referenznummer erstellen

Ein Körper ${}K$ heißt angeordnet, wenn es eine totale Ordnung ${}\geq$ auf ${}K$ gibt, die die beiden Eigenschaften

1. Aus ${}a\geq b$ folgt ${}a+c\geq b+c$ (für beliebige ${}a,b,c\in K$),
2. Aus ${}a\geq 0$ und ${}b\geq 0$ folgt ${}ab\geq 0$ (für beliebige ${}a,b\in K$),

erfüllt.

Statt ${}a\geq b$ schreibt man auch ${}b\leq a$. Die Schreibweise ${}a>b$ bedeutet ${}a\geq b$ und ${}a\neq b$. In einem angeordneten Körper nennt man ein Element ${}a\in K$ positiv, wenn ${}a>0$ ist, und negativ, wenn ${}a<0$ ist. Die ${}0$ ist demnach weder positiv noch negativ, und jedes Element ist entweder positiv oder negativ oder ${}0$. Die Elemente ${}a$ mit ${}a\geq 0$ nennt man dann einfach nichtnegativ und die Elemente ${}a$ mit ${}a\leq 0$ nichtpositiv. Für die entsprechenden Mengen schreibt man

$K_{+},\,K_{-},\,K_{\geq 0}=K_{+}^{0},\,K_{\leq 0}=K_{-}^{0}$

oder Ähnliches. Die wichtigsten Beispiele für angeordnete Körper sind der Körper der rationalen Zahlen ${}\mathbb {Q}$ und der Körper der reellen Zahlen ${}\mathbb {R}$.

Lemma Lemma 4.5 ändern

In einem angeordneten Körper gelten die folgenden Eigenschaften.

1. ${}1\geq 0$.
2. Es ist ${}a\geq 0$ genau dann, wenn ${}-a\leq 0$ ist.
3. Es ist ${}a\geq b$ genau dann, wenn ${}a-b\geq 0$ ist.
4. Es ist ${}a\geq b$ genau dann, wenn ${}-a\leq -b$ ist.
5. Aus ${}a\geq b$ und ${}c\geq d$ folgt ${}a+c\geq b+d$.
6. Aus ${}a\geq b$ und ${}c\geq 0$ folgt ${}ac\geq bc$.
7. Aus ${}a\geq b$ und ${}c\leq 0$ folgt ${}ac\leq bc$.
8. Aus ${}a\geq b\geq 0$ und ${}c\geq d\geq 0$ folgt ${}ac\geq bd$.
9. Aus ${}a\geq 0$ und ${}b\leq 0$ folgt ${}ab\leq 0$.
10. Aus ${}a\leq 0$ und ${}b\leq 0$ folgt ${}ab\geq 0$.

Beweis

Siehe Aufgabe 4.9.

$\Box$

Lemma Lemma 4.6 ändern

In einem angeordneten Körper gelten die folgenden Eigenschaften.

1. Aus ${}x>0$ folgt auch ${}x^{-1}>0$.
2. Aus ${}x<0$ folgt auch ${}x^{-1}<0$.
3. Für ${}x>0$ ist ${}x\geq 1$ genau dann, wenn ${}x^{-1}\leq 1$ ist.
4. Aus ${}x\geq y>0$ folgt ${}x^{-1}\leq y^{-1}$.
5. Für positive Elemente ${}x,y$ ist ${}x\geq y$ äquivalent zu ${}{\frac {x}{y}}\geq 1$.

Beweis

Siehe Aufgabe 4.11, Aufgabe 4., Aufgabe 4.12, Aufgabe 4.13 und Aufgabe 4.15.

$\Box$

Definition Referenznummer erstellen

Es sei ${}K$ ein angeordneter Körper. Zu ${}a,b\in K$, ${}a\leq b$, nennt man

• ${}[a,b]={\left\{x\in K\mid a\leq x{\text{ und }}x\leq b\right\}}$

das abgeschlossene Intervall.

• ${}]a,b[={\left\{x\in K\mid a<x{\text{ und }}x<b\right\}}$

das offene Intervall.

• ${}]a,b]={\left\{x\in K\mid a<x{\text{ und }}x\leq b\right\}}$

das linksseitig offene Intervall.

• ${}[a,b[={\left\{x\in K\mid a\leq x{\text{ und }}x<b\right\}}$

das rechtsseitig offene Intervall.

Für das offene Intervall wird häufig auch ${}(a,b)$ geschrieben. Die Zahlen ${}a$ und ${}b$ heißen die Grenzen des Intervalls, genauer spricht man von oberer und unterer Grenze. Die Bezeichnung linksseitig und rechtsseitig bei den beiden letzten Intervallen (die man auch als halboffen bezeichnet) rühren von der üblichen Repräsentierung der reellen Zahlen als Zahlengerade her, bei der rechts die positiven Zahlen stehen. Zutreffender (also weniger konventionsverhaftet) wäre es von „größerseitig offen“ und „kleinerseitig offen“ zu sprechen. Manchmal werden auch Schreibweisen wie ${}(a,\infty )$ verwendet. Dies bedeutet nicht, dass es in ${}K$ ein Element ${}\infty$ gibt, sondern ist lediglich eine kurze Schreibweise für ${}{\left\{x\in K\mid x>a\right\}}$. Diese Teilmengen nennt man auch unbeschränkte Intervalle, die Intervalle der Definition heißen auch genauer beschränkte Intervalle.

Bemerkung   Referenznummer erstellen

Ein äquivalenter Zugang zum Begriff des angeordneten Körpers funktioniert so: Man hat einen Körper ${}K$, bei dem eine Teilmenge ${}P\subseteq K$ (die „positive Hälfte“) ausgezeichnet ist mit den folgenden Eigenschaften

1. Entweder ${}x\in P$ oder ${}-x\in P$ oder ${}x=0$.
2. Aus ${}x,y\in P$ folgt ${}x+y\in P$.
3. Aus ${}x,y\in P$ folgt ${}x\cdot y\in P$.

In einem angeordneten Körper erfüllen die positiven Elemente diese Bedingungen. Man kann aber umgekehrt aus einem Körper mit einer solchen positiven Teilmenge einen angeordneten Körper machen, indem man

$x\geq y{\text{ durch }}x=y{\text{ oder }}x-y\in P$

definiert, siehe Aufgabe 4.37.

Der Betrag

Definition Referenznummer erstellen

In einem angeordneten Körper ${}K$ ist der Betrag eines Elementes ${}x\in K$ folgendermaßen definiert.

${}\vert {x}\vert ={\begin{cases}x,\,{\text{ falls }}x\geq 0\,,\\-x,\,{\text{ falls }}x<0\,.\end{cases}}\,$

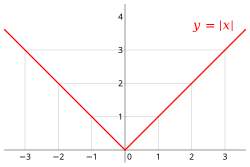
Der Betrag ist also nie negativ (da aus ${}x<0$ die Beziehung ${}-x>0$ folgt, vergleiche Aufgabe 4.7) und hat nur bei ${}x=0$ den Wert ${}0$, sonst ist er immer positiv. Die Gesamtabbildung

$K\longrightarrow K,\,x\longmapsto \vert {x}\vert ,$

nennt man auch Betragsfunktion. Der Funktionsgraph setzt sich aus zwei Halbgeraden zusammen; eine solche Funktion nennt man auch stückweise linear.

Lemma Referenznummer erstellen

Es sei ${}K$ ein angeordneter Körper.

Dann erfüllt die Betragsfunktion

$K\longrightarrow K,\,x\longmapsto \vert {x}\vert ,$

folgende Eigenschaften (dabei seien ${}x,y$ beliebige Elemente in ${}K$).

1. Es ist ${}\vert {x}\vert \geq 0$.
2. Es ist ${}\vert {x}\vert =0$ genau dann, wenn ${}x=0$ ist.
3. Es ist ${}\vert {x}\vert =\vert {y}\vert$ genau dann, wenn ${}x=y$ oder ${}x=-y$ ist.
4. Es ist ${}\vert {y-x}\vert =\vert {x-y}\vert$.
5. Es ist ${}\vert {xy}\vert =\vert {x}\vert \vert {y}\vert$.
6. Für ${}x\neq 0$ ist ${}\vert {x^{-1}}\vert =\vert {x}\vert ^{-1}$.
7. Es ist ${}\vert {x+y}\vert \leq \vert {x}\vert +\vert {y}\vert$ (Dreiecksungleichung für den Betrag).
8. Es ist ${}\vert {x+y}\vert \geq \vert {x}\vert -\vert {y}\vert$.

Beweis

Siehe Aufgabe 4.31.

$\Box$

Die Zahl ${}\vert {x-y}\vert$ nennt man auch den Abstand der beiden Zahlen ${}x$ und ${}y$.

Bernoulli'sche Ungleichung

Satz Referenznummer erstellen

Es sei ${}K$ ein angeordneter Körper und ${}n$ eine natürliche Zahl. Dann gilt für jedes ${}x\in K$ mit ${}x\geq -1$ die Abschätzung

${}(1+x)^{n}\geq 1+nx\,.$

Beweis

Wir führen Induktion über ${}n$. Bei ${}n=0$ steht beidseitig ${}1$, sodass die Aussage gilt. Es sei nun die Aussage für ${}n$ bereits bewiesen. Dann ist

${}{\begin{aligned}(1+x)^{n+1}&=(1+x)^{n}(1+x)\\&\geq (1+nx)(1+x)\\&=1+(n+1)x+nx^{2}\\&\geq 1+(n+1)x,\end{aligned}}$

da Quadrate (und positive Vielfache davon) in einem angeordneten Körper nichtnegativ sind.

$\Box$

Archimedisch angeordnete Körper

Wenn man sich wie üblich die reellen Zahlen als Zahlengerade vorstellt, so ist das nächste Axiom selbstverständlich. Es gibt aber auch sehr interessante angeordnete Körper, in denen dieses Axiom nicht gilt; es gilt auch nicht im Rahmen der sogenannten Nichtstandardanalysis.

Archimedes (ca. 287 -212 v. C.)

Definition Referenznummer erstellen

Es sei ${}K$ ein angeordneter Körper. Dann heißt ${}K$ archimedisch angeordnet, wenn das folgende Archimedische Axiom gilt, d.h. wenn es zu jedem ${}x\in K$ eine natürliche Zahl ${}n$ mit

${}n\geq x\,$

gibt.

Diese Eigenschaft ist für negative Elemente stets erfüllt, für positive Elemente handelt es sich aber um eine echte neue Bedingung, die nicht jeder angeordnete Körper erfüllt. Die rationalen Zahlen und die reellen Zahlen bilden jeweils einen archimedisch angeordneten Körper, ein nicht-archimedisch angeordneter Körper wird in Aufgabe 11.34 besprochen. Einen archimedisch angeordneten Körper kann man sich als eine Zahlengerade vorstellen, auf denen auch die ganzen Zahlen liegen. Mit Zahlengerade wird noch nichts genaues über „Lücken“ oder „Kontinuität“ behauptet.

Die folgende wichtige Aussage sollte man so lesen: Egal wie groß ${}y$ ist und egal wie klein ein positives ${}x$ ist, man kann stets mit hinreichend vielen ${}x$ die Zahl ${}y$ übertreffen. Egal wie kurz eine Strecke ist, wenn man sie hinreichend oft hintereinander legt, übertrifft man damit jede beliebig lange Strecke. Mit Sandkörnern beliebig kleiner Größe kann man eine beliebig große Sanddüne aufbauen.

Lemma Lemma 4.13 ändern

Es sei ${}K$ ein archimedisch angeordneter Körper.

Dann gibt es zu ${}x,y\in K$ mit ${}x>0$ stets ein ${}n\in \mathbb {N}$ mit ${}nx>y$.

Beweis

Wir betrachten ${}y/x$. Aufgrund des Archimedes-Axioms gibt es ein ${}n$ mit ${}n\geq y/x$. Da ${}x$ positiv ist, gilt nach Lemma 4.5  (6) auch ${}nx\geq y$.

$\Box$

Lemma Lemma 4.14 ändern

Es sei ${}K$ ein archimedisch angeordneter Körper. Es sei ${}x>0$.

Dann gibt es eine natürliche Zahl ${}n\in \mathbb {N}$ mit ${}{\frac {1}{n}}\leq x$.

Beweis

Es ist ${}x^{-1}$ eine nach Lemma 4.6  (1) positive Zahl und daher gibt es eine natürliche Zahl ${}n\in \mathbb {N}$ mit ${}n\geq x^{-1}>0$. Dies ist nach Lemma 4.6  (4) äquivalent zu

${}{\frac {1}{n}}=n^{-1}\leq {\left(x^{-1}\right)}^{-1}=x\,.$

$\Box$

Im folgenden Lemma verwenden wir, dass man zunächst die ganzen Zahlen ${}\mathbb {Z}$ in einem angeordneten Körper ${}K$ wiederfindet und dass man dann auch die rationalen Zahlen ${}\mathbb {Q}$ in ${}K$ wiederfindet. Die rationale Zahl ${}n/m$ ist als das Element ${}n_{K}\cdot (m_{K})^{-1}$ zu interpretieren, siehe auch Aufgabe 4.19.

Lemma Referenznummer erstellen

Es sei ${}K$ ein archimedisch angeordneter Körper.

Dann gibt es zwischen je zwei Elementen ${}x<y$ auch eine rationale Zahl ${}n/k$ (mit ${}n\in \mathbb {Z} ,\,k\in \mathbb {N} _{+}$) mit

${}x<{\frac {n}{k}}<y\,.$

Beweis

Wegen ${}y>x$ ist ${}y-x>0$ und daher gibt es nach Lemma 4.14 ein ${}k\in \mathbb {N}$ mit ${}{\frac {1}{k}}<y-x$. Nach Lemma 4.13 gibt es auch ein ${}n\in \mathbb {N}$ mit

${}n{\frac {1}{k}}>x\,$

und ein ${}n'\in \mathbb {Z} _{-}$ mit

${}n'{\frac {1}{k}}\leq x\,.$

Daher gibt es auch ein ${}n\in \mathbb {Z}$ derart, dass

$n{\frac {1}{k}}>x\,\,{\text{ und }}\,\,(n-1){\frac {1}{k}}\leq x$

ist. Damit ist einerseits

${}x<{\frac {n}{k}}\,$

und andererseits

${}{\frac {n}{k}}={\frac {n-1}{k}}+{\frac {1}{k}}<x+y-x=y\,$

wie gewünscht.

$\Box$

In einem archimedisch angeordneten Körper bilden die ganzzahligen Intervalle ${}[n,n+1[$, ${}n\in \mathbb {Z}$, eine disjunkte Überdeckung, d.h. es ist

${}K=\bigcup _{n\in \mathbb {Z} }[n,n+1[\,$

und ${}[m,m+1[\cap [n,n+1[=\emptyset$ für ${}m\neq n$ Deshalb ist die folgende Definition sinnvoll.

Definition Referenznummer erstellen

Es sei ${}K$ ein archimedisch angeordneter Körper und ${}x\in K$. Die Gaußklammer von ${}x$ ist durch

$\left\lfloor x\right\rfloor =n,{\text{ falls }}x\in [n,n+1[{\text{ und }}n\in \mathbb {Z} ,$

definiert.

Da die Werte der Gaußklammer die ganzen Zahlen sind, kann man die Gaußklammer auch als eine Abbildung ${}K\rightarrow \mathbb {Z}$ auffassen.

Lemma Lemma 4.17 ändern

Es sei ${}K$ ein archimedisch angeordneter Körper und ${}b>1$.

Dann gibt es zu jedem ${}S\in K$ eine natürliche Zahl ${}n\in \mathbb {N}$ mit

${}b^{n}\geq S\,.$

Beweis

Wir schreiben ${}b=1+u$ mit ${}u>0$. Aufgrund von Lemma 4.13 gibt es eine natürliche Zahl ${}n$ mit ${}nu\geq S-1$. Damit gilt unter Verwendung der Bernoulli-Ungleichung die Abschätzung

${}b^{n}=(1+u)^{n}\geq 1+nu\geq 1+S-1=S\,.$

$\Box$

Fußnoten