Kurs:Grundkurs Mathematik (Osnabrück 2022-2023)/Teil I/Vorlesung 24/kontrolle

Die Platzierung der rationalen Zahlen auf der Zahlengeraden

Man kann die rationalen Zahlen auf der Zahlengeraden platzieren (die ganzen Zahlen seien dort schon platziert). Die rationale Zahl ${}{\frac {a}{b}}$ mit ${}a,b\in \mathbb {N} _{+}$ findet man so: Man unterteilt die Strecke von ${}0$ nach ${}a$ in ${}b$ gleichlange Teilstrecken. Die Zahl ${}{\frac {a}{b}}$ ist dann die rechte Grenze des (von links) ersten Teilintervalls. Insbesondere ist ${}{\frac {1}{b}}$ die Länge des Intervalls, dass ${}b$-fach nebeneinander gelegt die Einheitsstrecke von ${}0$ bis ${}1$ (das Einheitsintervall) ergibt. Unter Bezugnahme auf elementargeometrische Eigenschaften der Ebene kann man diese Unterteilung folgendermaßen durchführen: Man betrachtet den linearen Graphen zum proportionalen Zusammenhang, der an der Stelle ${}a$ den Wert ${}b$ besitzt. Die Gerade, die senkrecht auf der ${}y$-Achse steht und durch den Punkt ${}(0,1)$ geht, trifft den Graphen in einem Punkt ${}(s,1)$, wobei ${}s$ die Länge der Verbindungsstrecke von ${}(0,1)$ zu ${}(s,1)$ ist. Aufgrund des Strahlensatzes, angewendet auf die Strahlen ${}y$-Achse und linearer Graph und die durch ${}y=1$ und ${}y=b$ gegebenen parallelen Geraden, gilt die Verhältnisgleichheit

${}{\frac {a}{b}}={\frac {s}{1}}\,.$

Die Streckenlänge ${}s$ kann man dann parallel auf die ${}x$-Achse verschieben, das Ergebnis ist der gesuchte Platz für ${}{\frac {a}{b}}$. Umgekehrt formuliert: Da das ${}b$-fache der Strecke von ${}0$ nach ${}1$ die Länge ${}b$ besitzt, ist das ${}b$-fache der Strecke ${}s$ gleich der Länge ${}a$. Achtung! Die Steigung des proportionalen Zusammenhangs (die Proportionalitätskonstante), der an der Stelle ${}a$ den Wert ${}b$ besitzt, ist ${}{\frac {b}{a}}$. Diese Zahl ergibt sich geometrisch, wenn man den Graphen mit der durch ${}x=1$ gegebenen Geraden (also die Gerade, die parallel zur ${}y$-Achse ist und durch den Punkt $(1,0)$ verläuft) schneidet, als Abstand zwischen dem Schnittpunkt und ${}(1,0)$.

Die geometrische Ausführung der vektoriellen Addition auf der Zahlengeraden. Man muss einen Zirkel einsetzen und parallele Geraden konstruieren können. Die ${}1$ spielt keine Rolle.

Die Addition und die Multiplikation lassen sich ebenfalls auf der Zahlengeraden geometrisch deuten bzw. durchführen. Die Addition von zwei Punkten ${}P$ und ${}Q$ ist die vektorielle Addition der Pfeile ${}{\overrightarrow {0P}}$ und ${}{\overrightarrow {0Q}}$, wobei der Startpunkt des einen Vektors parallel verschoben an den Endpunkt des anderen Vektors angelegt wird. Für positive Zahlen bedeutet das einfach, dass die zugehörigen, von ${}0$ ausgehenden Strecken aneinandergelegt werden. Die Korrektheit dieser Interpretation beruht (für rationale Zahlen) darauf, dass man die beiden Strecken als ganzzahlige Vielfache einer Vergleichsstrecke ${}{\overrightarrow {0R}}$ darstellen kann (Übergang zu einem Hauptnenner), also ${}{\overrightarrow {0P}}=m{\overrightarrow {0R}}$ und ${}{\overrightarrow {0Q}}=n{\overrightarrow {0R}}$ mit ${}m,n\in \mathbb {N}$ schreiben kann. Dann ist die Hintereinanderlegung der Strecken einfach ${}(m+n){\overrightarrow {0R}}$.

Für die geometrische Deutung der Multiplikation muss man den Strahlensatz heranziehen, man muss die ${}1$ fixiert haben und man muss Zirkel und Lineal zur Verfügung haben. Die zu multiplizierenden Punkte ${}a$ und ${}b$ seien auf der Zahlengerade gegeben, die wir als ${}x$-Achse in einem Koordinatensystem auffassen. Auf der ${}y$-Achse (man könnte auch eine andere Gerade durch den Nullpunkt nehmen) markieren wir den Punkt ${}a'$, der zum Nullpunkt den Abstand ${}a$ und somit die Koordinaten ${}(0,a)$ besitzt. Wir zeichnen die Gerade durch die beiden Punkte ${}(0,1)$ und ${}(b,0)$. Zu dieser Geraden zeichnen wir die parallele Gerade durch den Punkt ${}(0,a)$. Der Schnittpunkt dieser Geraden mit der ${}x$-Achse sei ${}(z,0)$. Mit dem Strahlensatz gilt dann die Beziehung ${}{\frac {z}{b}}={\frac {a}{1}}$, also ist

${}z=ab\,.$

Das Produkt ${}ab$ ist also der konstruierte Punkt ${}z$. Für den Nachweis der Korrektheit dieser geometrischen Multiplikation, die keinen Bezug auf den Strahlensatz nimmt, siehe Aufgabe 24.9.

Als Punkte auf der Zahlengeraden lassen sich rationale Zahlen ihrer Größe nach vergleichen. In der geometrischen Vorstellung bedeutet ${}x\geq y$ für beliebige Punkte ${}x$ und ${}y$ aus der rechten Hälfte der Zahlengeraden (dem positiven Zahlenstrahl), dass die Strecke ${}[0,x]$ in der Strecke ${}[0,y]$ enthalten ist, bzw., dass ${}y$ rechts von ${}x$ liegt. Für eine rationale Zahl wissen wir, dass ein ganzzahliges (geometrisches) Vielfaches davon, also die ${}n$-fache Hintereinanderlegung der Strecke, eine ganze Zahl ergibt. Für zwei rationale Zahlen ${}x$ und ${}y$ gibt es daher eine natürliche Zahl ${}n$ mit der Eigenschaft, dass sowohl ${}nx$ als auch ${}ny$ ganzzahlig sind. Damit können wir den Vergleich von rationalen Zahlen auf den Vergleich von ganzen Zahlen zurückführen. Wenn ${}x={\frac {a}{b}}$ und ${}y={\frac {c}{d}}$ mit ${}a,c\in \mathbb {Z}$ und ${}b,d\in \mathbb {N} _{+}$ ist, so kann man ${}n=bd$ nehmen und erhält die Beziehung

${}{\frac {a}{b}}\geq {\frac {c}{d}}\,$

genau dann, wenn in ${}\mathbb {Z}$ die Beziehung

${}ad\geq bc\,$

gilt. Hier begegnen wir wieder dem Überkreuzungsprinzip.

Die Ordnung auf den rationalen Zahlen

Wir definieren eine Anordnung auf den rationalen Zahlen.

Definition Definition 24.1 ändern

Auf den rationalen Zahlen ${}\mathbb {Q}$ wird die Größergleichrelation ${}\geq$ durch ${}{\frac {a}{b}}\geq {\frac {c}{d}}$ (bei positiven Nennern ${}b,d\in \mathbb {N} _{+}$), falls ${}ad\geq cb$ in ${}\mathbb {Z}$ gilt, definiert.

Wir müssen zuerst zeigen, dass diese Definition sinnvoll ist, also unabhängig von den gewählten Darstellungen der rationalen Zahlen als Brüche. Seien also

${}{\frac {a}{b}}={\frac {a'}{b'}}\,$

und

${}{\frac {c}{d}}={\frac {c'}{d'}}\,$

mit positiven Nennern. Dann ist

${}ab'=a'b\,$

und

${}cd'=c'd\,.$

Aus

${}ad\geq bc\,$

ergibt sich dann gemäß Lemma 19.13  (6) durch Multiplikation mit der positiven ganzen Zahl ${}b'd'$

${}adb'd'\geq bcb'd'\,.$

Dies schreiben wir als

${}a'dbd'\geq bc'b'd\,,$

woraus sich durch Kürzen mit der positiven ganzen Zahl ${}db$ die Abschätzung

${}a'd'\geq b'c'\,$

ergibt, die

${}{\frac {a'}{b'}}\geq {\frac {c'}{d'}}\,$

bedeutet. Wegen der Symmetrie der Situation gilt auch die Umkehrung. Die Beziehung ${}\geq$ ist also unabhängig von dem gewählten Bruchrepräsentanten. Die zugrunde liegende Idee ist, die beiden zu vergleichenden Brüche auf einen gemeinsamen positiven Nenner zu bringen und dann die Zähler zu vergleichen. Es ist

${}{\frac {a}{b}}={\frac {ad}{bd}}=ad\cdot {\frac {1}{bd}}\,$

und

${}{\frac {c}{d}}={\frac {cb}{bd}}=cb\cdot {\frac {1}{bd}}\,.$

Es liegt also einerseits das ${}ad$-Vielfache und andererseits das ${}cb$-Vielfache des gleichen Stammbruches ${}{\frac {1}{bd}}$. Es leuchtet ein, dass die Größerbeziehung nur von dem ganzzahligen Vorfaktor abhängt. Daraus und aus der Tatsache, dass man auch drei rationale Zahlen auf einen gemeinsamen Nenner bringen kann, folgt auch direkt, dass es sich um eine totale Ordnung handelt, siehe Aufgabe 24.36.

Beispiel Referenznummer erstellen

Wir wollen die rationalen Zahlen

${\frac {11}{7}},{\frac {3}{2}},{\frac {8}{5}},2$

miteinander vergleichen. Man kann alle diese Zahlen auf den gemeinsamen Nenner ${}70$ bringen, wodurch man die Darstellungen

${\frac {110}{70}},{\frac {105}{70}},{\frac {112}{70}},{\frac {140}{70}}$

erhält, aus denen man an den Zählern unmittelbar die Größenverhältnisse ablesen kann. Man kann auch die Brüche paarweise gemäß der Definition vergleichen, wegen

${}2\cdot 11=22\geq 21=3\cdot 7\,$

ist beispielsweise

${}{\frac {11}{7}}\geq {\frac {3}{2}}\,.$

Um die Ordnungseigenschaften der rationalen Zahlen leichter erfassen zu können, empfiehlt es sich, mit angeordneten Körpern zu arbeiten. Dies ist einfach ein angeordneter Ring, der zugleich ein Körper ist.

Definition Referenznummer erstellen

Ein Körper ${}K$ heißt angeordnet, wenn es eine totale Ordnung ${}\geq$ auf ${}K$ gibt, die die beiden Eigenschaften

1. Aus ${}x\geq y$ folgt ${}x+z\geq y+z$ (für beliebige ${}x,y,z\in K$),
2. Aus ${}x\geq 0$ und ${}y\geq 0$ folgt ${}xy\geq 0$ (für beliebige ${}x,y\in K$),

erfüllt.

Die beiden Eigenschaften heißen wieder die Verträglichkeit mit der Addition und die Verträglichkeit mit der Multiplikation. Es wird sich später herausstellen, dass auch die reellen Zahlen einen angeordneten Körper bilden. Elemente ${}x\in K$ mit ${}x>0$ heißen positiv und mit ${}x<0$ heißen negativ.

Satz Referenznummer erstellen

Die rationalen Zahlen ${}\mathbb {Q}$ bilden mit der in der Definition 24.1 festgelegten Ordnung

einen angeordneten Körper.

Beweis

Dass eine totale Ordnung vorliegt wird in Aufgabe 24.36 gezeigt. Es sei ${}x={\frac {a}{b}}$, ${}y={\frac {c}{d}}$ und ${}z={\frac {e}{f}}$ mit positiven Nennern ${}b,d,f$. Durch Übergang zu einem gemeinsamen Hauptnenner können wir direkt ${}b=d=f$ annehmen. Sei

${}x\geq y\,,$

also

${}a\geq c\,.$

Dann ist nach Lemma 19.11  (2) auch

${}a+e\geq c+e\,$

und somit ist

${}x+z={\frac {a}{b}}+{\frac {e}{b}}={\frac {a+e}{b}}\geq {\frac {c+e}{b}}={\frac {c}{b}}+{\frac {e}{b}}=y+z\,.$

Wenn die beiden Brüche ${}{\frac {a}{b}}$ und ${}{\frac {c}{d}}$ beide ${}\geq 0$ sind, so sind alle Zähler und Nenner aus ${}\mathbb {N}$ und dies überträgt sich auf ${}{\frac {ac}{bd}}$, also ist auch dies ${}\geq 0$.

$\Box$

Da ein angeordneter Körper insbesondere ein angeordneter Ring ist, gelten die Eigenschaften aus Lemma 19.13 unmittelbar auch für ${}\mathbb {Q}$ und für ${}\mathbb {R}$. Die dort angegebenen Regeln gelten bei einem angeordneten Körper auch dann, wenn man mit ${}>$ statt mit ${}\geq$ arbeitet. Wesentlich neue Aspekte bei einem angeordneten Körper treten in Bezug auf inverse Elemente auf.

Lemma Lemma 24.5 ändern

In einem angeordneten Körper gelten die folgenden Eigenschaften.

1. Aus ${}x>0$ folgt auch ${}x^{-1}>0$.
2. Aus ${}x<0$ folgt auch ${}x^{-1}<0$.
3. Für ${}x>0$ ist ${}x\geq 1$ genau dann, wenn ${}x^{-1}\leq 1$ ist.
4. Aus ${}x\geq y>0$ folgt ${}x^{-1}\leq y^{-1}$.
5. Für positive Elemente ${}x,y$ ist ${}x\geq y$ äquivalent zu ${}{\frac {x}{y}}\geq 1$.

Beweis

Siehe Aufgabe 24.15, Aufgabe 24.16, Aufgabe 24.17, Aufgabe 24.18 und Aufgabe 24.19.

$\Box$

Der Betrag

Definition Referenznummer erstellen

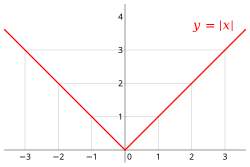
In einem angeordneten Körper ${}K$ ist der Betrag eines Elementes ${}x\in K$ folgendermaßen definiert.

${}\vert {x}\vert ={\begin{cases}x,\,{\text{ falls }}x\geq 0\,,\\-x,\,{\text{ falls }}x<0\,.\end{cases}}\,$

Der Betrag ist also nie negativ (da aus ${}x<0$ die Beziehung ${}-x>0$ folgt, vergleiche Lemma 19.13  (2)) und hat nur bei ${}x=0$ den Wert ${}0$, sonst ist er immer positiv. Die Gesamtabbildung

$K\longrightarrow K,\,x\longmapsto \vert {x}\vert ,$

nennt man auch Betragsfunktion. Der Funktionsgraph setzt sich aus zwei Halbgeraden zusammen; eine solche Funktion nennt man auch stückweise linear.

Lemma Lemma 24.7 ändern

Es sei ${}K$ ein angeordneter Körper.

Dann erfüllt die Betragsfunktion

$K\longrightarrow K,\,x\longmapsto \vert {x}\vert ,$

folgende Eigenschaften (dabei seien ${}x,y$ beliebige Elemente in ${}K$).

1. Es ist ${}\vert {x}\vert \geq 0$.
2. Es ist ${}\vert {x}\vert =0$ genau dann, wenn ${}x=0$ ist.
3. Es ist ${}\vert {x}\vert =\vert {y}\vert$ genau dann, wenn ${}x=y$ oder ${}x=-y$ ist.
4. Es ist ${}\vert {y-x}\vert =\vert {x-y}\vert$.
5. Es ist ${}\vert {xy}\vert =\vert {x}\vert \vert {y}\vert$.
6. Für ${}x\neq 0$ ist ${}\vert {x^{-1}}\vert =\vert {x}\vert ^{-1}$.
7. Es ist ${}\vert {x+y}\vert \leq \vert {x}\vert +\vert {y}\vert$ (Dreiecksungleichung für den Betrag).
8. Es ist ${}\vert {x+y}\vert \geq \vert {x}\vert -\vert {y}\vert$.

Beweis

Siehe Aufgabe 24.27.

$\Box$

Die Zahl ${}\vert {x-y}\vert$ nennt man auch den Abstand der beiden Zahlen ${}x$ und ${}y$ und die Länge der Strecke (oder des Intervalls) von ${}x$ nach ${}y$ bzw. von ${}y$ nach ${}x$. Bei ${}x<y$ wird die Strecke von ${}x$ nach ${}y$ in ${}n$ (${}n\in \mathbb {N} _{+}$) gleichlange Streckenabschnitte eingeteilt, wenn man die Zwischenpunkte

$x+i{\frac {y-x}{n}},i=0,1,\ldots ,n$

betrachtet (bei ${}i=0$ bzw. ${}i=n$ ergeben sich Randpunkte).

Das arithmetische Mittel

Definition Referenznummer erstellen

Zu ${}n$ Zahlen ${}a_{1},\ldots ,a_{n}$ in einem angeordneten Körper ${}K$ nennt man

${\frac {a_{1}+a_{2}+\cdots +a_{n}}{n}}$

das arithmetische Mittel der Zahlen.

Für zwei Zahlen ${}x<y$ in einem angeordneten Körper gilt

${}x<{\frac {x+y}{2}}<y\,,$

siehe Aufgabe 24.30. Dies bedeutet insbesondere, dass es zwischen je zwei Zahlen in einem angeordneten Körper noch eine weitere Zahl dazwischen gibt. Da man dieses Argument beliebig oft wiederholen kann, gibt es zwischen je zwei Zahlen unendlich viele weitere Zahlen. In jeder beliebig kleinen positiven Umgebung eines Elementes gibt es unendlich viele Elemente.

Die Bernoullische Ungleichung

Die folgende Aussage heißt Bernoullische Ungleichung.

Lemma Referenznummer erstellen

Es sei ${}K$ ein angeordneter Körper und ${}n$ eine natürliche Zahl. Dann gilt für jedes ${}x\in K$ mit ${}x\geq -1$ die Abschätzung

${}(1+x)^{n}\geq 1+nx\,.$

Beweis

Wir führen Induktion über ${}n$. Bei ${}n=0$ steht beidseitig ${}1$, sodass die Aussage gilt. Es sei nun die Aussage für ${}n$ bereits bewiesen. Dann ist

${}{\begin{aligned}(1+x)^{n+1}&=(1+x)^{n}(1+x)\\&\geq (1+nx)(1+x)\\&=1+(n+1)x+nx^{2}\\&\geq 1+(n+1)x,\end{aligned}}$

da Quadrate (und positive Vielfache davon) in einem angeordneten Körper nichtnegativ sind.

$\Box$