Konvexkombination

Veranschaulichung einer Konvexkombination 1., 2. und 3. Ordnung in Geogebra 

Konvexkombination in 3D mit 4 Vektoren

Einführung

Gegebenen sei ein reeller Vektorraum $(V,+,\cdot ,\mathbb {R} )$. Eine Linearkombination heißt Konvexkombination, wenn alle Koeffizienten $\lambda _{i}\in [0,1]$ aus dem Einheitsintervall [0,1] stammen und die Summe aller $\lambda _{i}$ für die Vektoren $v_{i}\in V$ mit $i\in \{1,\ldots ,n\}$ 1 ergibt:

${\begin{array}{rcl}v&=&\lambda _{1}v_{1}+\lambda _{2}v_{2}+\dotsb +\lambda _{n}v_{n}\\&=&\sum _{i=1}^{n}\lambda _{i}v_{i},\\&{\mbox{mit}}&0\leq \lambda _{i}\leq 1,\quad \sum _{i=1}^{n}\lambda _{i}=1\,.\end{array}}$

Konvexkombinationen in der Ebene

Wenn man Konvexkombinationen in der Ebene betrachtet, ist der zugrundeliegende Vektorraum der zweidimensionalen Raum $V:=\mathbb {R} ^{2}$. Zunächst betrachten wir in $\mathbb {R} ^{2}$ Konvexkombinationen von zwei Vektoren. Durch die Bedingung $\lambda _{1}+\lambda _{2}=1$ sind beide Skalare voneinander abhängig. Ist $t\in [0,1]$, dann setzt man z.B. $\lambda _{1}:=(1-t)$ und $\lambda _{2}:=t$.

Konvexkombinationen als Abbildungen in den Vektorraum

Betrachtet man nun eine Abbildung $K\colon [0,1]\to V$, so kann man allgemein Konvexkombinationen 1. Ordnung von 2 Vektoren $v_{1},v_{2}\in V$ wie folgt über die Abbildung $K$ darstellen:

$K(t):=(1-t)\cdot v_{1}+t\cdot v_{2}$

Animation einer Konvexkombination von zwei Vektoren als Abbildung

Konvexkombination als Abbildung in einer GIF-Animation

Konvexkombinationen von 2 Vektoren in Funktionenräumen

Die Behandlung von Konvexkombination mit $v_{1},v_{2}\in \mathbb {R} ^{2}$ oder $v_{1},v_{2},v_{3}\in \mathbb {R} ^{3}$ liefert eine Veranschaulichung im Vektorräume aus der Sekundarstufe II als spezielle Linearkombinationen. Konvexkombinationen kann man aber auch auf Funktionenräume angewendet werden. Z.B. seien $f,g\in V:={\mathcal {C}}([a,b],\mathbb {R} )$, so entsteht mit $\lambda _{1},\lambda _{2}\in [0,1]$ und $\lambda _{1}+\lambda _{2}=1$ eine neue Funktion $h_{t}\in V$ mit:

$h_{t}:=(1-t)\cdot f+t\cdot g$

Der Index $t$ in $h_{t}$ wird verwendet, da in Abhängigkeit von $t$ eine andere Funktion $h_{t}$ definiert wird.

Beispiel für Konvexkombinationen von Funktionen

Sei $[a,b]=[4,7]$ und als erste Funktion $f:[a,b]\to \mathbb {R}$ wird ein Polynom definiert.

$f(x):={\frac {3}{10}}\cdot x^{2}-2$

Als zweite Funktion wird eine trigonometrische Funktion $g:[a,b]\to \mathbb {R}$ gewählt.

$g(x):=2\cdot cos(x)+1$

Die folgende Abbildung veranschaulicht die Konvexkombination $K(t):=(1-t)\cdot f+t\cdot g$

Animation für Konvexkomobinationen von Funktionen

Die folgende Animation zeigt mehrere Konvexkombinationen von zwei gegebenen Funktionen.

Konvexkombination von zwei Funktionen in Geogebra

Geogebra: Interaktives Applet - Download: Geogebra-File

Bemerkung - Deformation

Wenn die erste Funktion $f$ die Ausgangsform beschreibt und $g$ die Zielform, kann man Konvexkombinationen z.B. in der Computer-Graphik für die Deformation einer Ausgangsform in eine Zielform beschreiben.

Konvexkombinationen von Konvexkombinationen

In der obigen Animation sieht man eine Konvexkombination von 2 Vektoren in der Ebene oder in einem Funktionenraum betrachtet. Verwendet man drei Punkte so kann man zwischen jeweils zwei Punkten eine Konvexkombination 1. Ordnung erstellen. Wir werden nun Konvexkombinationen höherer Ordnung betrachten, indem man z.B. aus zwei Konvexkombinationen 1. Ordnung eine Konvexkombination 2. Ordnung konstruiert. Allgemein enstehen aus 2 Konvexkombination der Ordnung $n$ eine Konvexkombinationen der Ordnung $n+1$.

Konvexe Hülle

Die Menge aller Konvexkombinationen einer vorgegebenen Menge von Vektoren bezeichnet man als konvexe Hülle (siehe auch p-konvex Hülle).

Video Konvexkombinationen in der Ebene

Geogebra: Interaktives Applet - Download: Geogebra-File

Bemerkungen Video über Konvexkombinationen der Ordnung 1, 2 und 3 in Geogebra

In dem Video sieht man Konvexkombinationen der

• 1. Ordnung zwischen $A_{1}$ und $B_{1}$ ohne Hilfspunkte,
• 2. Ordnung zwischen $A_{2}$ und $B_{2}$ mit dem Hilfspunkt $S_{1}$,
• 3. Ordnung zwischen $A_{3}$ und $B_{3}$ mit den Hilfspunkten $H_{1},H_{2}$,

Konvexkombinationen als Polynome von t

Konvexkombination können als Polynome aufgefasst werden, bei denen die Koeffizienten aus einem Vektorraum $(V,+,\cdot ,\mathbb {R} )$ stammen (siehe auch Polynomalgebra). Wählt man z.B. $V:=\mathbb {R} ^{n}$ kann man eine Konvexkombinationen $K$ als Element der Polynomalgebra $V[t]$ auffassen.

3D-Konvexkombination - 1. Ordnung

Wählt man z.B. $n=3$ und $V:=\mathbb {R} ^{3}$, so ist eine Konvexkombination 1. Ordnung wie folgt definiert

$A={\begin{pmatrix}1\\2\\4\end{pmatrix}},\,B={\begin{pmatrix}4\\1\\0\end{pmatrix}},\,\,K(t):=(1-t)\cdot A+t\cdot B=(B-A)\cdot t+A$

Eine Konvexkombination 1. Ordnung liefert also ein Polynom mit dem Grad 1. mit dem Argument $t$. Stellen Sie die Konvexkombination in Geogebra 3D mit $t\in [0,1]$ dar (siehe auch Darstellung einer Geraden durch Richtungsvektor und Ortsvektor).

3D-Konvexkombination - 2. Ordnung

Wählt man wieder $n=3$ und $V:=\mathbb {R} ^{3}$ mit einem Hilfpunkt $H_{1}\in V$, so liefern zwei Konvexkombinationen 1. Ordnung die Konvexkombinationen 2. Ordnung.

$H_{1}={\begin{pmatrix}2\\2\\2\end{pmatrix}},{\begin{array}{rcl}K_{(1,1)}(t)&:=&(H_{1}-A)\cdot t+A\\K_{(1,2)}(t)&:=&(B-H_{1})\cdot t+H_{1}\\K_{2}(t)&:=&((H_{1}-A)\cdot t+A)\cdot (1-t)+((B-H_{1})\cdot t+H_{1})\cdot t\end{array}}$

Stellen Sie $K_{2}$ als Polynom $K_{2}(t)=P_{2}\cdot t^{2}+P_{1}\cdot t^{1}+P_{0}\cdot t^{0}$ dar.

Koeffizienten

Man erhält damit für die Koeffizientenvektoren:

• $P_{0}=A$
• $P_{1}=2\cdot (H_{1}-A)$
• $P_{2}=B-2H_{1}+A$

Aufgabe für Studierende

• Berechnen Sie nun für $n=3$ ($n=4,5,...$) die Koeffizienten in $P_{k}\in V=\mathbb {R} ^{3}$.
• Welches System für die Berechnung der Koeffizienten können Sie bzgl. Anfangs, Endpunkt und den Hilfpunkten entdecken?

Bernsteinpolynom - Ordnung 1

${\begin{array}{rcl}K_{1}(t)&:=&A\cdot (1-t)+B\cdot t\\&=&A\cdot (1-t)^{1}\cdot t^{0}+B\cdot (1-t)^{0}\cdot t^{1}\\\end{array}}$

Berechnung des Polynoms - Ordnung 2

${\begin{array}{rcl}K_{2}(t)&:=&((H_{1}-A)\cdot t+A)\cdot (1-t)+((B-H_{1})\cdot t+H_{1})\cdot t\\&=&(H_{1}\cdot t-A\cdot t+A)-(H_{1}\cdot t^{2}-A\cdot t^{2}+A\cdot t)\\&&+(B\cdot t^{2}-H_{1}\cdot t^{2}+H_{1}\cdot t)\\&=&(B-2\cdot H_{1}+A)\cdot t^{2}+2\cdot (H_{1}-A)\cdot t+A\end{array}}$

Bernsteinpolynom - Ordnung 2

${\begin{array}{rcl}K_{2}(t)&:=&((H_{1}-A)\cdot t+A)\cdot (1-t)+((B-H_{1})\cdot t+H_{1})\cdot t\\&=&A\cdot (1-t)^{2}+2\cdot H_{1}\cdot t\cdot (1-t)+B\cdot t^{2}\end{array}}$

Bernsteinpolynoms - Ordnung 3

${\begin{array}{rcl}K_{3}(t)&:=&A\cdot (1-t)^{3}+3\cdot H_{1}\cdot (1-t)^{2}\cdot t+3\cdot H_{2}\cdot (1-t)\cdot t^{2}+B\cdot t^{3}\end{array}}$

Aufgabe: Berechnung des Polynoms - Ordnung 3

• Berechnen Sie das Polynom 3 Grades und leiten Sie daraus die allgemeine Formel für die Koeffizienten von $t^{n}$. Verwenden Sie dazu die Notation $H_{0}:=A$ und $H_{n}:=B$ für Konvexkombinationen der Ordnung $n$ zwischen den Punkten $A$ und $B$ mit den Hilfpunkten $H_{1},\ldots ,H_{n-1}$.
• Beweisen Sie Ihre Vermutung durch vollständige Induktion.

$K_{n}(t):=\sum _{k=0}^{n}{n \choose k}\cdot H_{k}\cdot t^{k}\cdot (1-t)^{n-k}$

Interaktives Geogebra-Arbeitsblatt

Das Video zeigt eine Interaktion mit dem obigen Konvexkombinationen. Aus Geogebra heraus wurde das erstellte Arbeitsblatt auf die Geogebra-Materialienseite hochgeladen. Dies können Sie direkt im Browser unter folgendem Link nutzen:

Interaktives Arbeitsblatt: Konvexkombination auf Geogebra

Konvexkombination als Abbildung

Eine Konvexkombination kann für die Interpolation von Punkten $A=v_{1}$ und $B=v_{n}$ verwendet werden. Seinen ferner die Hilfspunkte $H_{1}=v_{2}$,....$H_{n_{1}}=v_{n-1}$ für eine Konvexkombination $n$-ter Ordnung gegeben. Die Konvexkombinationen kann man allgemein als Abbildung von dem Intervall $[0,1]$ nach $\mathbb {R} ^{n}$ wie folgt auffassen:

${\begin{array}{rcl}K_{n}:&[0,1]&\rightarrow &\mathbb {R} ^{n}\\&t&\mapsto &\displaystyle \sum _{k=0}^{n}{n \choose k}(1-t)^{n-k}\cdot t^{k}\cdot v_{k+1}\\&&&={n \choose 0}(1-t)^{n}v_{1}+{n \choose 1}(1-t)^{n-1}tv_{2}+\ldots +{n \choose n}t^{n}v_{n}\end{array}}$

Konvexkombinatioen in Geogebra - Download

In Geogebra kann man die geometrische Bedeutung der Konvexkombinationen dynamisch visualisieren. Unter dem

• GitHub-Repository können Sie
• Beispieldateien von Konvexkombinatioen für Geogebra als ZIP-Datei herunterladen
• Das GitHub-Repository enthält ferner eine wxMaxima Datei für die algebraische Berechnung der Punkte, die auf der Konvexkombination liegen. Dort sind auch Datenpunkte aus dem $\mathbb {R} ^{3}$ eingebaut, die zeigen, dass man die gesamte Konstruktion der Konvexkombinatione auch auf den $\mathbb {R} ^{3}$ bzw. den $\mathbb {R} ^{n}$ übertragen kann.

In den Beispieldateien werden Konvexkombinationen von zwei Punkten (Vektoren $v_{1},v_{2}\in \mathbb {R} ^{2}$) behandelt.

Definition der Konvexkombinationen als Abbildungen/Kurven im Vektorraum

Konvexkombination 1. Ordnung

• Konvexkombination 1. Ordnung erzeugen alle Punkte auf der Verbindungsstrecke zwischen den zwei Punkten $v_{1},v_{2}\in \mathbb {R} ^{2}$.

$K_{1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot v_{1}+\lambda \cdot v_{2}$

Konvexkombination 2. Ordnung

• Eine Konvexkombination 2. Ordnung entsteht mit einem weiteren Hilfpunkte $h_{1}\in \mathbb {R} ^{2}$ in der Ebene aus den folgenden beiden Konvexkombinationen 1.Ordnung:

$K_{1,1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot v_{1}+\lambda \cdot h_{1}$ (Konvexkombination 1. Ordnung zwischen $v_{1},h_{1}\in \mathbb {R} ^{2}$)

$K_{1,2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot h_{1}+\lambda \cdot v_{2}$ (Konvexkombination 1. Ordnung zwischen $h_{1},v_{2}\in \mathbb {R} ^{2}$)

$K_{2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{1,1}(\lambda )+\lambda \cdot K_{1,2}(\lambda )$ (Konvexkombination 2. Ordnung zwischen $v_{1},v_{2}\in \mathbb {R} ^{2}$ mit dem Hilfpunkt $h_{1}\in \mathbb {R} ^{2}$)

Konvexkombination 3. Ordnung

Eine Konvexkombination 3. Ordnung entsteht mit zwei weiteren Hilfpunkte $h_{1},h_{2}\in \mathbb {R} ^{2}$ in der Ebene aus den folgenden drei Konvexkombinationen 1.Ordnung:

$K_{1,1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot v_{1}+\lambda \cdot h_{1}$ (Konvexkombination 1. Ordnung zwischen $v_{1},h_{1}\in \mathbb {R} ^{2}$)

$K_{1,2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot h_{1}+\lambda \cdot h_{2}$ (Konvexkombination 1. Ordnung zwischen $h_{1},h_{2}\in \mathbb {R} ^{2}$)

$K_{1,3}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot h_{2}+\lambda \cdot v_{2}$ (Konvexkombination 1. Ordnung zwischen $h_{2},v_{2}\in \mathbb {R} ^{2}$)

Konvexkombinationen 2. Ordnung aus KK der 1. Ordung

Aus den drei Konvexkombinatioen 1. Ordnung konstruiert man zwei Konvexkombination 2. Ordnung wie folgt:

$K_{2,1}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{1,1}(\lambda )+\lambda \cdot K_{1,2}(\lambda )$ (Konvexkombination 2. Ordnung zwischen $v_{1},h_{2}\in \mathbb {R} ^{2}$ mit dem Hilfpunkt $h_{1}\in \mathbb {R} ^{2}$)

$K_{2,2}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{1,2}(\lambda )+\lambda \cdot K_{1,3}(\lambda )$ (Konvexkombination 2. Ordnung zwischen $h_{1},v_{2}\in \mathbb {R} ^{2}$ mit dem Hilfpunkt $h_{2}\in \mathbb {R} ^{2}$)

Konvexkombinationen 3. Ordnung aus KK der 2. Ordung

Aus den beiden Konvexkombinationen 2. Ordnung entsteht nun eine Konvexkombination 3. Ordnung wie folgt:

$K_{3}:[0,1]\rightarrow \mathbb {R} ^{2},\qquad \lambda \mapsto (1-\lambda )\cdot K_{2,1}(\lambda )+\lambda \cdot K_{2,2}(\lambda )$ (Konvexkombination 2. Ordnung zwischen $v_{1},v_{2}\in \mathbb {R} ^{2}$ mit den Hilfpunkten $h_{1},h_{2}\in \mathbb {R} ^{2}$)

Konvexkombinationen n-ter Ordnung

Allgemein hat eine Konvexkombination $n$-ter Ordnung

• $n-1$ Hilfspunkte $h_{1},\ldots ,h_{n_{1}}$
• $n$ Konvexkombinationen 1. Ordnung,
• $n-1$ Konvexkombinationen 2. Ordnung,
• ...
• $n-k$ Konvexkombinationen $(k+1)$-ter Ordnung,
• ...
• $1$ Konvexkombination n-ter Ordnung,

In der 3D-Graphik sind insbesondere die Konvexkombinationen 3. Ordnung von Bedeutung (siehe Bezier-Kurven)

Konvexkombination von Funktionen

Sei $\mathbb {D}$ ein Definitionbereich von Funktionen und $(V,+,*,\mathbb {K} )$ ein Vektorraum über dem Körper $\mathbb {K}$ (z.B. $\mathbb {K} :=\mathbb {R} ,\mathbb {C}$ und ${\mathcal {C}}(\mathbb {D} ,V)$ die Menge der stetigen Funktionen von $\mathbb {D}$ nach $V$. Eine Konvexkombination von zwei stetigen Funktionen $f,g\in {\mathcal {C}}(\mathbb {D} ,V)$ mit $\lambda \in [0,1]\subset \mathbb {K}$ ist definiert durch:

$h_{\lambda }:=(1-\lambda )\cdot f+\lambda \cdot g$

mit

${\begin{array}{rcl}h_{\lambda }:\mathbb {D} &\to &V\\z&\mapsto &h_{\lambda }(z):=(1-\lambda )\cdot f(z)+\lambda \cdot g(z)\\\end{array}}$

Konvexkombinationen aus mehr als 2 Vektoren

Im obigen Fall wurde zwei Vektoren aus dem zugrundeliegenden Vektorraum als Konvexkombination untersucht und auch Konvexkombinationen höherer Ordnung konstruiert. Nun wird das Vorgehen auf mehr als 2 Vektoren erweitert, wobei wieder ein Parametrisierung über Vektoren $(t_{1},\ldots ,t_{n})\in [0,1]^{n}$ erfolgt.

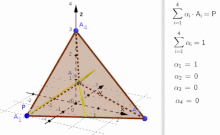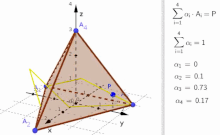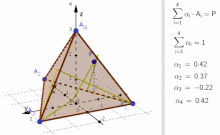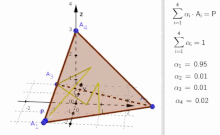
Konvexkombinationen aus 3 Vektoren

Erweitern Sie den Ansatz auf Konvexkombination mit zwei Parametern $t_{1},t_{2}\in [0,1]$ und Vektoren $v_{1},v_{2},v_{2}$ über:

$\lambda _{1}:=(1-t_{1}),\,\lambda _{2}:=t_{1}\cdot (1-t_{2}),\,\lambda _{3}:=t_{1}\cdot t_{2}$

und der Abbildung für die Konvexkombinationen in das abgeschlossene Dreieck, das durch die drei Vektoren $v_{1},v_{2},v_{2}$ als Extremalpunkte definiert wird:

$K_{3}(t_{1},t_{2}):=\underbrace {(1-t_{1})} _{=\lambda _{1}}\cdot v_{1}+\underbrace {t_{1}\cdot (1-t_{2})} _{=\lambda _{2}}\cdot v_{2}+\underbrace {t_{1}\cdot t_{2}} _{=\lambda _{3}}\cdot v_{3}$

Konvexkombinationen aus 4 Vektoren

Für 4 Vektoren verwendet man wieder als Parametrisierung $(t_{1},t_{2})\in [0,1]\times [0,1]$

$\lambda _{1}:=(1-t_{1})\cdot (1-t_{2}),\,\lambda _{2}:=t_{1}\cdot (1-t_{2}),$

$\lambda _{3}:=(1-t_{1})\cdot t_{2},\,\lambda _{4}:=t_{1}\cdot t_{2}$

Die Abbildung $K_{4}:[0,1]^{2}\to V$ stellt dann alle Vektoren aus der konvexe Hülle von $v_{1},v_{2},v_{3},v_{4}\in V$ dar.

$K_{4}(t_{1},t_{2}):=\underbrace {(1-t_{1})(1-t_{2})} _{=\lambda _{1}}\cdot v_{1}+\underbrace {t_{1}(1-t_{2})} _{=\lambda _{2}}\cdot v_{2}+\underbrace {(1-t_{1})t_{2}} _{=\lambda _{2}}\cdot v_{3}+\underbrace {t_{1}\cdot t_{2}} _{=\lambda _{4}}\cdot v_{3}$

Aufgabe

• (Geogebra) Analysieren Sie die Geogebra-Beispieldateien und beschreiben Sie die Bedeutung der Hilfspunkte für die Form der Ortslinie in der Dynamischen Geometrie-Software (DGS) Geogebra.
• Welche Rolle spielen die Hilfspunkte, um differenzierbare Interpolationen zu erzeugen (Tangentialvektoren)?
• (Interpolation) Vergleichen Sie die Interpolationen nach Lagrange bzw. Newton für viele Datenpunkte mit der Interpolation durch mehrere Konvexkombinationen 3. Ordnung. Welche Stärken und Schwächen (Oszillation zwischen den Datenpunkten) haben die unterschiedlichen Verfahren. Veranschaulichen Sie diese mit Geogebra.

Aufgabe - 3. Ordnung und funktionale Darstellung

• (Konvexkombination 3-ter Ordnung) Berechnen Sie die Punkte von Konvexkombinationen 3. Ordnung im $\mathbb {R} ^{3}$ mit Maxima CAS (siehe auch Maxima Tutorial der FH-Hagen).

K(t):= A * (1-t)^3 + H1 * (1-t)^2 * t + H2 * (1-t) * t^2 + B * t^3

Definieren Sie die Punkte als 3x1-Matrizen mit:

A : matrix( [-1], [3], [-4] )

• (Unterschied Konvexkombination 3er Ordnung und kubischen Splines) Analysieren Sie Gemeinsamkeiten und Unterschiede von kubischen Splines und Konvexkombinationen 3er Ordnung! Was ist der Anwendungskontext von kubischen Splines? Wann würden Sie Konvexkombinationen verwenden?

Aufgabe - Konvexkombinationen von Funktionen

• (Konvexkombination von Funktionen) Wählen Sie $\mathbb {D} :=\mathbb {R}$ $V:=\mathbb {R}$ und stellen die Konvexkombination von $f$ und $g$ in Geogebra mit einem Schieberegler $\lambda$ (analog zur GIF-Animation), wobei $f(x)=x^{2}$ und $g(x)=cos(x)$ ist. Was beobachten Sie, wenn Sie den Schieberegler von 0 auf 1 bewegen? $g(x)=cos(x)$ ist beschränkt und $f(x)=x^{2}$ ist unbeschränkt auf $\mathbb {D} :=\mathbb {R}$. Welche Eigenschaft hat $h_{\lambda }$ für $0<\lambda <1$?
• (Konvexkombinationen und Polynomalgebren) Fassen Sie die Konvexkombination der Ordnung $n$ mit Koeffizienten aus einem Vektorraum nach Potenzen von $t^{n}$ zusammen und betrachten Sie die Koeffizienten aus dem Vektorraum $V$ allgemein. Wie werden die Koeffizienten der Polynome aus den Punkten bzw. Hilfspunkten für die Potenzen gebildet? (siehe auch Polynomalgebra und Bezierkurven)

Aufgabe - Bernsteinpolynome und De-Casteljau-Algorithmus

• (Bernsteinpolynome) Analysieren Sie den Zusammenhang von Konvexkombinationen als spezielle Linearkombinationen aus der Linearen Algebra mit Bernsteinpolynomen und Bezierkurven. Bernsteinpolynome für einen bestimmten Grad $n\in \mathbb {N}$ stellen eine Zerlegung der Eins dar. Welchen Zusammenhang besteht bzgl. einer Zerlegung der Eins bei den Konvexkombinationen. Welche Bedeutung hat dabei eine polynomial Darstellung in Bezug auf die Zerlegung der 1

$\lambda _{1}+\ldots +\lambda _{n}=\sum _{k=1}^{n}\lambda _{k}=1$

• (De-Casteljau-Algorithmus) Analysieren Sie den De-Casteljau-Algorithmus und erläutern Sie, welche Rolle die Bernsteinpolynomen als Kontrollpolynome für die definierenden Punkte der Kurve darstellen.

Interpolationen

Konvexkombinationen können auch für die Interpolation von Polynomen verwendet werden. Starten Sie zunächst mit Interpolationen der ersten Ordnung, indem die Punkte mit Geraden der Form $f_{k}(x):=m_{k}\cdot x+b_{k}$ interpoliert werden. Dabei sind die Punkte $\mathbb {D} :=\{(x_{0},y_{0}),\ldots ,(x_{n},y_{n})\}$ Datenpunkte gegeben, die mit den Funktionen $f_{k}(x):=m_{k}\cdot x+b_{k}$ stückweise Interpoliert werden. Berechnen Sie aus den Konvexkombinationen $P_{k}(t)\in \mathbb {R} ^{2}$ die funktionale Darstellung $f_{k}:[x_{k-1},x_{k}]\to \mathbb {R}$ mit $f_{k}(x):=m_{k}\cdot x+b_{k}$:

$P_{k}(t):=(1-t)\cdot {\begin{pmatrix}x_{k-1}\\y_{k-1}\end{pmatrix}}+t\cdot {\begin{pmatrix}x_{k}\\y_{k}\end{pmatrix}}$

Berechnung von t in Abhängigkeit von x

Gegeben sei $x\in [x_{k-1},x_{k}]\subset \mathbb {R}$. Wir berechnen nun das zugehörige $t\in [0,1]$ für die Konvexkombination mit der Vorüberlegung, dass $t=0$ für $x=x_{k-1}$ und $t=1$ für $x=x_{k}$ sein soll. Die folgende Abbildung übernimmt die lineare Transformation $T:[x_{k-1},x_{k}]\to [0,1]$.

$T(x):={\frac {x-x_{k-1}}{x_{k}-x_{k-1}}}$

Berechnung des Funktionswertes zu x

Die Konvexkombination

$P_{k}(t):=(1-t)\cdot {\begin{pmatrix}x_{k-1}\\y_{k-1}\end{pmatrix}}+t\cdot {\begin{pmatrix}x_{k}\\y_{k}\end{pmatrix}}$

liefert den Interpolationspunkt des Graphen. Man benötigt allerdings nur die y-Koordinate des zugehörigen Interpolationspunktes $P_{k}(t)={\begin{pmatrix}(1-t)\cdot x_{k-1}+t\cdot x_{k}\\(1-t)\cdot y_{k-1}+t\cdot y_{k}\end{pmatrix}}$. Also verwenden wir den folgende Term: $(1-t)\cdot y_{k-1}+t\cdot y_{k}$.

CAS4Wiki

Mit CAS4Wiki kann die Spur der dreidimensionalen Konvexkombination der Ordnung 3 geplottet werden.

CAS4Wiki Commands

Funktionale Darstellung

Durch Einsetzen für $t\in [0,1]$ erhält man die lineare Interpolationsfunktion $f_{k}:[x_{k-1},x_{k}]\to \mathbb {R}$ über:

$f_{k}(x):={\bigg (}1-\underbrace {\frac {x-x_{k-1}}{x_{k}-x_{k-1}}} _{=t}{\bigg )}\cdot y_{k-1}+{\bigg (}\underbrace {\frac {x-x_{k-1}}{x_{k}-x_{k-1}}} _{=t}{\bigg )}\cdot y_{k}$.

Aufagben

• Berechnen Sie die Koeffizienten $m_{k},b_{k}\in \mathbb {R}$ der Funktion $f_{k}:[x_{k-1},x_{k}]\to \mathbb {R}$ mit $f_{k}(x):=m_{k}\cdot x+b_{k}$!
• Übertragen Sie diese Interpolation auf Konvexkombination der Ordnung 3 und überlegen Sie, wie Sie in Abhängigkeit von den Datenpunkten die beiden Hilfspunkte der Interpolation wählen müssen, damit die Interpolation differenzierbar ist und in der Darstellung differenzierbare Übergänge zwischen den Interpolationspunkten generiert.
• Welche geometrischen Eigenschaften müssen Hilfspunkte zwischen zwei benachbarten Interpolationsintervallen für die Differnzierbarkeit besitzen.

Interpolation mit Konvexkombination der Ordnung 3

Geogebra: Interaktives Applet - Download: Geogebra-File

Geogebra: Interaktives Applet - Download: Geogebra-File

Aufgabe für Studierende

Entwickeln Sie für die folgenden eine mathematische/algebraische Beschreibung durch Terme:

• Die grün gestichelte Linien sind Konvexkombinationen 1. Ordnung,
• An den Knotenpunkten des offenen Polygonzuges erstellen Sie eine Winkelhalbierende (konstruktiv kann man das durch eine Raute umsetzen, wobei zwei Seiten und ein Eckpunkt durch zwei benachbarte Strecken im Polygonzug definiert sind).
• Erstellen Sie eine Orthogonale durch den Verbindungspunkt von zwei benachbarten Strecken im Polygonzug.
• Analysieren Sie die Abbildung oben und legen Sie die nächsten Schritte für die Festlegung der beiden Hilfspunkte für eine Konvexkombination 3. Ordnung fest. Das Vorgehen ist nicht eindeutig insbesondere an den Randpunkte des Polygonzuges. Was spricht für Ihre Wahl der mathematischen Umsetzung?

Nutzen Sie insgesamt Methoden aus der Lineare Algebra (z.B. Skalarprodukt,... für die vektorielle Beschreibung des obigen geometrischen Vorgehens.

Morphing und die Nutzung von Konvexkombinationen

Im folgenden Abschnitt werden wir Transformationen von Bilder im Kontext von Konvexkombinationen betrachten. Beim Morphing gibt es zahlreiche mathematische Werkzeuge. Hier werden nur Aspekte im Kontext von Konvexkombinationen betrachtet.

Konvexkombination für Graustufenbilder

Betrachten Sie die obige GIF-Animation und nehmen Sie zunächst zwei unterschiedliche Schwarzweißbilder und transformieren Sie pixelweise die Graufstufenwerte (schwarz=0,...255=weiß) von einem Pixel aus Bild 1 zu einem Pixel in Bild 2 (Umsetzung z.B. in Octave Image Processing v7.3.0 bzw. Octave Image Processing v5.2.0. Beachten Sie dabei, dass die Konvexkombinationen reellwertige Helligkeitswerte in den Graustufen liefern, die Sie auf ganzzahlige Werte runden müssen (z.B. 232,423 auf 232 = annähernd weiß)

Konvexkombination für Farbbilder

• Übertragen Sie das Vorgehen nur auf Farbbilder, wobei Sie Farbwerte für die Grundfarben in ähnlicher Weise von Graustufenwerten auf Farbwerte übertragen werden.
• Eine große digitale Farbpalette wird dabei Anteil von drei Grundfarben kodiert (z.B. Rot, Grün, Blau RGB. Unterscheiden sich Farben, kann man z.B. die Konvexkombinationen auf die einzelnen Grundfarben anwenden.

Räumliche Bewegung von Pixeln

• In der obigen Morphing-Animation werden aber nicht nur statisch pixelweise konvex kombiniert, sondern für fest definierte Punkte, wie z.B. Augen findet auch ein räumlicher Transformationsprozess statt. Überlegen Sie sich, wie z.B. das Zentrum der Iris im Auge räumlich von einem Bild1 in das Bild2 verschoben wird.
• Verbinden Sie nun räumliche Transformationsprozesse mit einer Farbanpassung der Pixel, dass sich also ein Pixel vom Ort $(x_{1},y_{1})$ in der Bildmatrix nach $(x_{2},y_{2})$ bewegt und sich auf dem Weg von $(x_{1},y_{1})$ nach $(x_{2},y_{2})$ die Farbe von gelb nach blau wechselt.

Siehe auch

• Konvexkombinationen
• p-konvexe Hülle
• Kurs:Mathematische Modellbildung
• Extremalpunkt
• Konvexkombination interaktiv in GeogebraTube
• Integrationswege in der Funktionentheorie
• Hilbertraum
• Konvexkombination und Interpolation auf Dreiecken in der Ebene
• Satz von Rouché in der Funktionentheorie
• Polynomalgebra
• Bernsteinpolynomen
• Bezierkurven
• De-Casteljau-Algorithmus
• Kurs:Maßtheorie auf topologischen Räumen
• Morphing

Wiki2Reveal - Folien

• absolut p-konvexe Hülle - (Foliensatz)

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Funktionalanalysis' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Konvexkombination
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.