Kurs:Elemente der Algebra (Osnabrück 2015)/Vorlesung 27/kontrolle
- Das Delische Problem

Wir kommen zur ersten Konsequenz von unserer systematischen Untersuchung der konstruierbaren Zahlen auf die klassischen Konstruktionsprobleme.
Die Würfelverdopplung mit Zirkel und Lineal ist nicht möglich.
Wir betrachten einen Würfel mit der Kantenlänge und dem Volumen . Die Konstruktion eines Würfels mit dem doppelten Volumen würde bedeuten, dass man die neue Kantenlänge, also mit Zirkel und Lineal konstruieren könnte. Das Minimalpolynom von ist , da dieses offenbar annulliert und nach Lemma 6.9 irreduzibel ist, da in keine dritte Wurzel aus existiert. Nach Korollar 26.7 ist nicht konstruierbar, da keine Zweierpotenz ist.
- Die Quadratur des Kreises
Es ist nicht möglich, zu einem vorgegebenen Kreis ein flächengleiches Quadrat mit Zirkel und Lineal zu konstruieren.
Wenn es ein Konstruktionsverfahren gäbe, so könnte man insbesondere den Einheitskreis mit dem Radius quadrieren, d.h. man könnte ein Quadrat mit der Seitenlänge mit Zirkel und Lineal konstruieren. Nach Korollar 26.6 muss aber eine konstruierbare Zahl algebraisch sein. Nach dem Satz von Lindemann ist aber und damit auch transzendent.
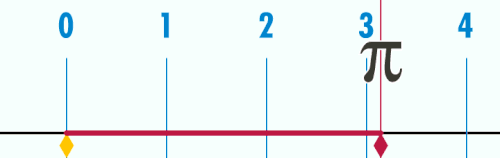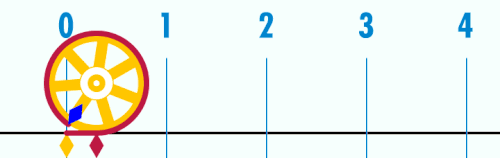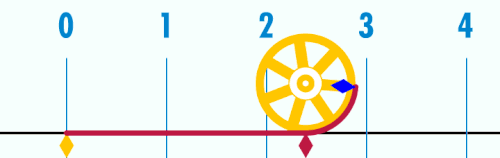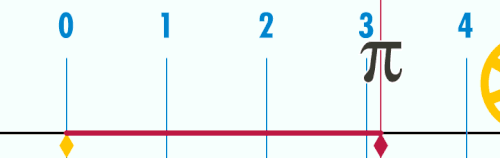
Es gibt natürlich einige geometrische Methoden die Zahl zu erhalten, z.B. die Abrollmethode und die Schwimmbadmethode.
Man kann die Zahl auch mit Hilfe von Schwimmbecken und einer idealen Flüssigkeit erhalten.
-
Wir starten mit einem Einheitskreis,
-
den wir als Grundfläche
-
eines Schwimmbeckens der Höhe 1 nehmen.
-
Das füllen wir randvoll mit Wasser auf.
-
Wir nehmen ein zweites Schwimmbecken mit quadratischer Grundfläche und Höhe 4.
-
Der Inhalt des ersten Schwimmbeckens wird
-
in das zweite Schwimmbecken gegossen.
-
Der Wasserstand im zweiten Schwimmbecken ist exakt .
- Einheitswurzeln
Die ist für jedes eine -te Einheitswurzel, und die ist für jedes gerade eine -te Einheitswurzel. Es gibt maximal -te Einheitswurzel, da das Polynom maximal Nullstellen besitzt. Die Einheitswurzeln bilden also insbesondere eine endliche Untergruppe (mit und ist auch , usw.) der Einheitengruppe des Körpers. Nach einem Satz, den wir nicht bewiesen haben, ist diese Gruppe zyklisch mit einer Ordnung, die teilt.
Eine -te Einheitswurzel heißt primitiv, wenn sie die Ordnung besitzt.
Man beachte, dass ein Erzeuger der Gruppe der Einheitswurzeln nur dann primitiv heißt, wenn es verschiedene Einheitswurzeln gibt. Wenn eine primitive -te Einheitswurzel ist, so sind genau die mit und teilerfremd zu die primitiven Einheitswurzeln. Insbesondere gibt es, wenn es überhaupt primitive Einheitswurzeln gibt, genau primitive Einheitswurzeln, wobei die eulersche -Funktion bezeichnet. Die komplexen Einheitswurzeln lassen sich einfach beschreiben.
Es sei .
Die Nullstellen des Polynoms über sind
In gilt die Faktorisierung
Der Beweis verwendet einige Grundtatsachen über die komplexe Exponentialfunktion. Es ist
Die angegebenen komplexen Zahlen sind also wirklich Nullstellen des Polynoms . Diese Nullstellen sind alle untereinander verschieden, da aus
mit sofort, durch Betrachten des Quotienten, folgt, und daraus
Es gibt also explizit angegebene Nullstellen und daher müssen dies alle Nullstellen des Polynoms sein. Die explizite Beschreibung in Koordinaten folgt aus der eulerschen Formel.
- Kreisteilungskörper
Offenbar ist eine Nullstelle von . Daher kann man durch teilen und erhält, wie man schnell nachrechnen kann,
Wegen ist daher der -te Kreisteilungskörper auch der Zerfällungskörper von
Es gibt auch Kreisteilungskörper über anderen Körpern, da es ja stets Zerfällungskörper gibt. Wir beschränken uns aber weitgehend auf die Kreisteilungskörper über , die wir auch mit bezeichnen. Da auf die in Lemma 27.7 beschriebenen Art über in Linearfaktoren zerfällt, kann man als Unterkörper von realisieren, und zwar ist der von allen -ten Einheitswurzeln erzeugte Unterkörper von . Dieser wird sogar schon von einer einzigen primitiven Einheitswurzel erzeugt. Wir erwähnen den folgenden Begriff.
Es sei . Dann wird der -te Kreisteilungskörper über
von erzeugt.
Der -te Kreisteilungskörper ist also
Insbesondere ist jeder Kreisteilungskörper eine einfache Körpererweiterung von .[1]
Es sei der -te Kreisteilungskörper über . Wegen ist . Wegen gehören auch alle anderen Einheitswurzeln zu , also ist .
Statt kann man auch jede andere -te primitive Einheitswurzel aus als Erzeuger nehmen.
Wir bestimmen einige Kreisteilungskörper für kleine . Bei oder ist der Kreisteilungskörper gleich . Bei ist
und der zweite Faktor zerfällt
Daher ist der dritte Kreisteilungskörper der von erzeugte Körper, es ist also eine quadratische Körpererweiterung der rationalen Zahlen.
Bei ist natürlich
Der vierte Kreisteilungskörper ist somit , also ebenfalls eine quadratische Körpererweiterung von .
Der Beweis der folgenden wichtigen Aussage beruht auf Überlegungen, die wir nicht entwickelt haben.
Es sei eine Primzahl.
Dann ist der -te Kreisteilungskörper gleich
Insbesondere besitzt der -te Kreisteilungskörper den Grad über .
Der -te Kreisteilungskörper wird nach Lemma 27.10 von erzeugt, er ist also isomorph zu , wobei das Minimalpolynom von bezeichnet. Als Einheitswurzel ist eine Nullstelle von und wegen ist eine Nullstelle von . Das Polynom ist irreduzibel nach Aufgabe ***** {{:Kurs:Kurs:Elemente der Algebra (Osnabrück 2015)/X^(p-1)+...+X+1/Irreduzibel/Aufgabe/Aufgabereferenznummer/X^(p-1)+...+X+1/Irreduzibel/Aufgabe/Aufgabereferenznummer}} und daher handelt es sich nach Lemma 23.2 (2) um das Minimalpolynom von .
Der fünfte Kreisteilungskörper wird von der komplexen Zahl erzeugt. Er hat aufgrund von Lemma 27.12 die Gestalt
wobei die Variable als (oder eine andere primitive Einheitswurzel) zu interpretieren ist. Sei und setze . Aus Symmetriegründen muss dies eine reelle Zahl sein. Es ist
Es ist also (die positive Wurzel) und somit haben wir eine Folge von quadratischen Körpererweiterungen
Satz 26.5, dass die fünften Einheitswurzeln konstruierbare Zahlen sind.
- ↑ Dies ist natürlich auch klar aufgrund des Satzes vom primitiven Element.




































![{\displaystyle {}{\mathbb {C} }[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c156a1899277cd3bf3b7edc239bc1abafd7339a7)

















![{\displaystyle {}K_{n}=\mathbb {Q} {\left(e^{2\pi {\mathrm {i} }/n}\right)}=\mathbb {Q} [e^{2\pi {\mathrm {i} }/n}]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ece165e2dd0accec8769a7733007b5c6d0877d1)

![{\displaystyle {}\mathbb {Q} [e^{2\pi {\mathrm {i} }/n}]\subseteq K_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/318575a9a9df381ec43af702522354bc1d139997)

![{\displaystyle {}\mathbb {Q} [e^{2\pi {\mathrm {i} }/n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/246c0bcb2ec55d485d332858b47ccd53452e4863)
![{\displaystyle {}\mathbb {Q} [e^{2\pi {\mathrm {i} }/n}]=K_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09b41856b277e5aa9a815ac6a036b3a1a2d1e4a9)






![{\displaystyle {}K_{3}=\mathbb {Q} [{\sqrt {-3}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3c48f47205652b1996549ddee7d25a377fc72a)


![{\displaystyle {}\mathbb {Q} [{\mathrm {i} }]\cong \mathbb {Q} [X]/(X^{2}+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b8a786122ace13cebc63fb93e867dd4899f6103)

![{\displaystyle \mathbb {Q} [X]/{\left(X^{p-1}+X^{p-2}+\cdots +X^{1}+1\right)}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bb395dce1a03319a37e3f9d72a17d76b00f50c4)


![{\displaystyle {}\mathbb {Q} [X]/(P)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7369caea1836766330690c5aa3c8645858412ae7)






![{\displaystyle {}K_{5}\cong \mathbb {Q} [X]/{\left(X^{4}+X^{3}+X^{2}+X+1\right)}\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/051950e76f1d361aeec28f7e056fd2a550af98e0)





![{\displaystyle {}\mathbb {Q} \subset \mathbb {Q} [{\sqrt {5}}]\subset K_{5}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd7414defe26557472f916f61ad919318296c6c9)