Trigonometrische Funktionen/R/Inverse Funktionen/Analytische Eigenschaften/Textabschnitt
induziert eine bijektive, streng wachsende Funktion
![{\displaystyle [-\pi /2,\pi /2]\longrightarrow [-1,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/527f8bc31212ec82e3778cde36b1ed32192bf657)
und die reelle Kosinusfunktion induziert eine bijektive streng fallende Funktion
![{\displaystyle [0,\pi ]\longrightarrow [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbd9728b307c63938254cd4e4aff49bc8e2f2a7)
Beweis
Siehe
Aufgabe.
Die reelle Tangensfunktion induziert eine bijektive, streng wachsende Funktion
![{\displaystyle ]-\pi /2,\pi /2[\longrightarrow \mathbb {R} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f54b80848470e2b293193379bd774648a7d69df6)
und die reelle Kotangensfunktion induziert eine bijektive streng fallende Funktion
![{\displaystyle ]0,\pi [\longrightarrow \mathbb {R} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ee76be0ff249a9e5158134ec10b2585d1deacb1)
Beweis
Siehe
Aufgabe.
Aufgrund der Bijektivität von Sinus, Kosinus, Tangens und Kotangens auf geeigneten Intervallen gibt es die folgenden Umkehrfunktionen.
![{\displaystyle [-1,1]\longrightarrow [-{\frac {\pi }{2}},{\frac {\pi }{2}}],\,x\longmapsto \arcsin x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c24a8a90340b8ae29506b60069c96a906c84497)
![{\displaystyle [-1,1]\longrightarrow [0,\pi ],\,x\longmapsto \arccos x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/204deb80b68913b620eba6f2a76dd3db16804d7a)
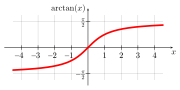
![{\displaystyle \mathbb {R} \longrightarrow ]-{\frac {\pi }{2}},{\frac {\pi }{2}}[,\,x\longmapsto \arctan x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa0f4921b59ab4688759dda8d4bbf7ccb8deab26)
![{\displaystyle \mathbb {R} \longrightarrow ]0,\pi [,\,x\longmapsto \operatorname {arccot} x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d619690f844a8f2dba9e0c98f4850e0b255be06a)
Die inversen trigonometrischen Funktionen besitzen die folgenden Ableitungen.
Für den Arkustangens gilt beispielsweise nach Fakt
