Kurs:Mathematik (Osnabrück 2009-2011)/Teil II/Arbeitsblatt 40

Aufwärmaufgaben

Aufgabe

Bestimme die Ableitung der Kurve

$f\colon \mathbb {R} \longrightarrow \mathbb {R} ^{3},\,t\longmapsto f(t)={\left(t^{2}-\sin t,e^{-t}+2t^{3},t\cdot \sinh t+{\frac {1}{t^{2}+1}}\right)},$

in jedem Punkt ${}t\in \mathbb {R}$.

Aufgabe

Skizziere die Bilder und die Graphen der folgenden Kurven im ${}\mathbb {R} ^{2}$.

1. ${}t\longmapsto {\left(t^{2},t^{2}\right)}$,
2. ${}t\longmapsto {\left(t^{2},-t^{2}\right)}$,
3. ${}t\longmapsto {\left(t^{2},t\right)}$,
4. ${}t\longmapsto {\left(2t,3t\right)}$,
5. ${}t\longmapsto {\left(t^{2},t^{3}\right)}$.

Aufgabe

Es sei ${}V$ ein euklidischer Vektorraum und ${}v,w\in V$. Zeige, dass die Abbildung

$f\colon \mathbb {R} \longrightarrow V,\,t\longmapsto tv+w,$

differenzierbar ist mit der Ableitung ${}f'(t)=v$.

Aufgabe

Es sei ${}I$ ein reelles Intervall und ${}V$ ein euklidischer Vektorraum. Es seien

$f,g\colon I\longrightarrow V$

zwei in ${}t_{0}\in I$ differenzierbare Kurven und es sei

$h\colon I\longrightarrow \mathbb {R}$

eine in ${}t_{0}$ differenzierbare Funktion. Zeige, dass folgende Aussagen gelten.

1. Die Summe

   $f+g\colon I\longrightarrow V,\,t\longmapsto f(t)+g(t),$

   ist in ${}t_{0}$ differenzierbar mit

   ${}(f+g)'(t_{0})=f'(t_{0})+g'(t_{0})\,.$

2. Das Produkt

   $hf\colon I\longrightarrow V,\,t\longmapsto h(t)f(t),$

   ist differenzierbar in ${}t_{0}$ mit

   ${}(hf)'(t_{0})=h(t_{0})f'(t_{0})+h'(t_{0})f(t_{0})\,.$

   Insbesondere ist für ${}c\in \mathbb {R}$ auch ${}cf$ differenzierbar in ${}t_{0}$ mit

   ${}(cf)'(t_{0})=cf'(t_{0})\,.$

3. Wenn ${}h$ nullstellenfrei ist, so ist auch die Quotientenfunktion

   ${\frac {f}{h}}\colon I\longrightarrow V,\,t\longmapsto {\frac {f(t)}{h(t)}},$

   in ${}t_{0}$ differenzierbar mit

   ${}{\left({\frac {f}{h}}\right)}'(t_{0})={\frac {h(t_{0})f'(t_{0})-h'(t_{0})f(t_{0})}{(h(t_{0}))^{2}}}\,.$

Die folgenden Aufgaben wiederholen wichige Eigenschaften von euklidischen Vektorräumen.

Aufgabe

Man beweise das Schmidtsche Orthonormalisierungsverfahren. Das besagt, dass man in einem euklidischen Vektorraum aus einer gegebenen Basis ${}v_{1},\ldots ,v_{n}$ eine Orthonormalbasis ${}u_{1},\ldots ,u_{n}$ basteln kann derart, dass die erzeugten Unterräume

${}\langle v_{1},\ldots ,v_{i}\rangle =\langle u_{1},\ldots ,u_{i}\rangle \,$

übereinstimmen für alle ${}i=1,\ldots ,n$.

Aufgabe

Es sei ${}V$ ein Vektorraum über ${}\mathbb {R}$ mit einem Skalarprodukt ${}\left\langle -,-\right\rangle$ und der zugehörigen Norm ${}\Vert {-}\Vert$. Zeige, dass die sogenannte Parallelogrammgleichung

${}\Vert {v+w}\Vert ^{2}+\Vert {v-w}\Vert ^{2}=2\Vert {v}\Vert ^{2}+2\Vert {w}\Vert ^{2}\,$

gilt.

Aufgabe

Es seien ${}(V_{1},\left\langle -,-\right\rangle _{1})$ und ${}(V_{2},\left\langle -,-\right\rangle _{2})$ zwei euklidische Vektorräume. Zeige, dass durch

$\left\langle (v_{1},v_{2}),(w_{1},w_{2})\right\rangle :=\left\langle v_{1},w_{1}\right\rangle _{1}+\left\langle v_{2},w_{2}\right\rangle _{2}$

ein Skalarprodukt auf dem Produktraum ${}V_{1}\times V_{2}$ definiert wird.

Aufgabe

Es sei ${}(M,d)$ ein metrischer Raum, sei ${}T\subseteq M$ eine Teilmenge und sei ${}a\in M$ ein Berührpunkt von ${}T$. Es sei

$f\colon T\longrightarrow V$

eine Abbildung in einen euklidischen Vektorraum ${}V$ mit den Komponentenfunktionen

$f_{1},\ldots ,f_{n}\colon T\longrightarrow \mathbb {R}$

bezüglich einer Basis von ${}V$. Zeige, dass der Limes

$\operatorname {lim} _{x\rightarrow a}\,f(x)$

genau dann existiert, wenn sämtliche Limiten

$\operatorname {lim} _{x\rightarrow a}\,f_{j}(x)$

existieren.

Aufgaben zum Abgeben

Aufgabe (3 Punkte)

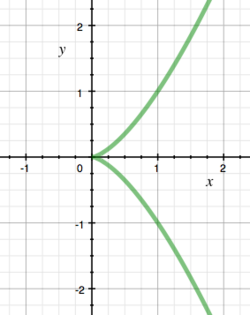
Das Bild der durch

$\mathbb {R} \longrightarrow \mathbb {R} ^{2},\,t\longmapsto \left(t^{2},\,t^{3}\right),$

definierten Kurve heißt Neilsche Parabel. Zeige, dass ein Punkt ${}(x,y)\in \mathbb {R} ^{2}$ genau dann zu diesem Bild gehört, wenn er die Gleichung ${}x^{3}=y^{2}$ erfüllt.

Aufgabe (4 Punkte)

Wir betrachten die Abbildung

$f\colon \mathbb {R} \longrightarrow S^{1}\subseteq \mathbb {R} ^{2},$

die einem Punkt ${}t\in \mathbb {R}$ den eindeutigen Schnittpunkt ${}\neq (0,-1)$ der durch die beiden Punkte ${}(t,1)$ und ${}(0,-1)$ gegebenen Geraden ${}G_{t}$ mit dem Einheitskreis

${}S^{1}={\left\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\right\}}\,$

zuordnet. Zeige, dass diese Abbildung wohldefiniert ist und bestimme die funktionalen Ausdrücke, die diese Abbildung beschreiben. Zeige, dass ${}f$ differenzierbar ist. Ist ${}f$ injektiv, ist ${}f$ surjektiv?

Aufgabe (3 Punkte)

Für welche Punkte ${}t\in \mathbb {R}$ ist der Abstand der Bildpunkte der Kurve

$\mathbb {R} \longrightarrow \mathbb {R} ^{2},\,t\longmapsto (2\sin t,3\cos t),$

zum Nullpunkt ${}(0,0)$ maximal, für welche minimal?

Aufgabe (4 Punkte)

Betrachte die Kurve

$f\colon \mathbb {R} \longrightarrow \mathbb {R} ^{3},\,x\longmapsto \left(x^{2}-x,\,x^{3}+\sinh x,\,\sin(x^{2})\right).$

a) Bestimme die Ableitung von ${}f$ in jedem Punkt ${}x$.

b) Bestimme die Komponentenfunktionen von ${}f$ bezüglich der neuen Basis

$(1,0,3),(2,4,6),(1,-1,0)$

von ${}\mathbb {R} ^{3}$.

c) Berechne die Ableitung in der neuen Basis direkt und mit Hilfe von Lemma 40.8.

Aufgabe (4 Punkte)

Es sei ${}P\in \mathbb {R} ^{n}$ ein Punkt und sei ${}I={]{-1},1[}$. Wir betrachten die Menge

${}M={\left\{f:I\rightarrow \mathbb {R} ^{n}\mid f{\text{ differenzierbar}},\,f(0)=P\right\}}\,.$

Wir nennen zwei Kurven ${}f,g\in M$ tangential äquivalent, wenn

${}f'(0)=g'(0)\,$

ist.

a) Zeige, dass dies eine Äquivalenzrelation ist.

b) Finde den einfachsten Vertreter für die Äquivalenzklassen.

c) Man gebe für jede Klasse einen weiteren Vertreter an.

d) Beschreibe die Menge der Äquivalenzklassen (also die Quotientenmenge).