Kurs:Zahlentheorie (Osnabrück 2016-2017)/Vorlesung 10

Pythagoreische Tripel

Definition

Ein pythagoreisches Tripel ist eine ganzzahlige Lösung ${}(x,y,z)\in \mathbb {Z} ^{3}$ der diophantischen Gleichung

{}x^{2}+y^{2}=z^{2}\,.

Es heißt primitiv, wenn ${}x,y,z$ keinen gemeinsamen Teiler besitzen.

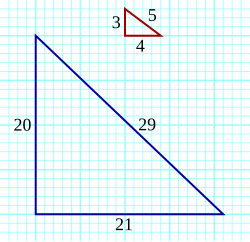
Lösungstripel, bei denen (mindestens) ein Eintrag ${}0$ ist, heißen trivial. Nach der Umkehrung des Satzes des Pythagoras bildet ein solches Tripel die Seitenlängen eines rechtwinkligen Dreieckes. Es geht also um rechtwinklige Dreiecke mit der Eigenschaft, dass alle drei Seiten eine ganzzahlige Länge haben (dabei sind ${}x,y$ die Seitenlängen der Katheten und ${}z$ ist die Seitenlänge der Hypotenuse). Das bekannteste pythagoreische Tripel ist zweifellos ${}(3,4,5)$ . Wenn zwei Zahlen davon einen gemeinsamen Teiler haben, so hat natürlich auch die dritte diesen Teiler, und das Tripel ist nicht primitiv.

Ferner sind ${}x$ und ${}y$ nicht zugleich ungerade, siehe Aufgabe 10.1.

Wir wollen alle (primitiven) pythagoreischen Tripel finden. Man kann das Problem umformulieren, indem man durch ${}z^{2}$ teilt. Dann ist das Problem äquivalent zu:

Bestimme alle rationalen Lösungen für die Gleichung

r^{2}+s^{2}=1\,\,(r,s\in {\mathbb {Q} }).

Es geht also um alle Punkte auf dem Einheitskreis (in der Ebene mit Mittelpunkt ${}(0,0)$ und Radius ${}1$ , deren beide Koordinaten rationale Zahlen sind. Die trivialen Lösungen sind die komplexen Zahlen ${}1,{\mathrm {i} },-1,-{\mathrm {i} }$ .

Bemerkung

Der (Einheits-)Kreis ist ein eindimensionales Objekt und es gibt verschiedene (Teil-)Parametrisierungen für ihn, etwa durch

x\longmapsto {\left(x,{\sqrt {1-x^{2}}}\right)},

oder die trigonometrische Parametrisierung

t\longmapsto (\cos(t),\sin(t)),

Hier brauchen wir aber eine Parametrisierung, die rationale Zahlen in solche Punkte überführt, deren beide Koordinaten rational sind.

Wir betrachten hierzu die Abbildung, die einen Punkt ${}t$ auf der ${}y$ -Achse auf den Durchstoßungspunkt ${}(x,y)$ abbildet, den der Einheitskreis mit der durch ${}(0,t)$ und ${}(-1,0)$ definierten Geraden bildet. Aufgrund des Strahlensatzes haben wir die Bedingung

{}{\frac {t}{1}}={\frac {y}{1+x}}\,

bzw. ${}y=t(1+x)$ . Setzt man diese Gleichung in die Gleichung des Einheitskreises ein, so erhält man

{}1=x^{2}+y^{2}=x^{2}+t^{2}(x+1)^{2}\,

und damit

{}0=(x^{2}-1)+t^{2}(x+1)^{2}=(x+1){\left((x-1)+t^{2}(x+1)\right)}\,.

Da uns die erste Lösung ${}x=-1$ nicht interessiert, betrachten wir den zweiten Faktor

{}0=(x-1)+t^{2}(x+1)=x(1+t^{2})+t^{2}-1\,,

die zu

x={\frac {1-t^{2}}{1+t^{2}}}\,\,\,{\text{ und }}\,\,\,y=t\cdot (x+1)=t\cdot {\left({\frac {1-t^{2}}{1+t^{2}}}+1\right)}={\frac {2t}{1+t^{2}}}

führt. Die Abbildung

t\longmapsto {\left({\frac {1-t^{2}}{1+t^{2}}},{\frac {2t}{1+t^{2}}}\right)}=(x,y)

ist also eine rationale Parametrisierung des Einheitskreises.

Wir fassen zusammen:

Satz

Die Abbildung

\mathbb {Q} \longrightarrow S_{\mathbb {Q} }^{1},\,t\longmapsto \left({\frac {1-t^{2}}{1+t^{2}}},\,{\frac {2t}{1+t^{2}}}\right)=(x,y),

von der Menge der rationalen Zahlen in die Menge der Punkte auf dem Einheitskreis mit rationalen Koordinaten ist injektiv, und mit der Ausnahme von ${}(-1,0)$ liegt jeder Punkt im Bild.

Beweis

Dies wurde bereits oben bewiesen, die Injektivität ist klar von der geometrischen Interpretation her und ist als Aufgabe 10.4 zu beweisen.

\Box

Korollar

Die Menge der Punkte auf dem Einheitskreis mit rationalen Koordinaten bilden eine dichte Teilmenge.

Beweis

Die Parametrisierung

\varphi \colon \mathbb {R} \longrightarrow S^{1},\,t\longmapsto \varphi (t)=\left({\frac {1-t^{2}}{1+t^{2}}},\,{\frac {2t}{1+t^{2}}}\right),

ist stetig, da sie komponentenweise durch rationale Funktionen gegeben ist. Es sei ${}s\in S^{1}$ ein Punkt des Einheitskreises. Der Punkt ${}s=(-1,0)$ (der Punkt, der von der Parametrisierung nicht erfasst wird), ist selbst rational. Es sei also ${}s\neq (-1,0)$ , und sei ${}t\in \mathbb {R}$ eine reelle Zahl mit ${}\varphi (t)=s$ . Es sei ${}\epsilon >0$ vorgegeben. Aufgrund der Stetigkeit gibt es dann auch ein ${}\delta >0$ derart, dass die Ballumgebung ${}B(t,\delta )$ nach ${}B(s,\epsilon )$ hinein abgebildet wird, also ${}\varphi (B(t,\delta ))\subseteq B(s,\epsilon )$ . Da die rationalen Zahlen innerhalb der reellen Zahlen dicht liegen, gibt es eine rationale Zahl ${}q\in B(t,\delta )$ . Dann ist ${}\varphi (q)$ ein Punkt auf dem Einheitskreis mit rationalen Koordinaten, der in der ${}\epsilon$ -Umgebung von ${}s$ liegt.

\Box

Die Formeln des folgenden Satzes zur Berechnung der pythagoreischen Tripel heißen auch indische Formeln.

Satz

Es sei ${}(x,y,z)$ ein pythagoreisches Tripel mit ${}y$ gerade und mit ${}z\neq -x$ .

Dann gibt es eindeutig bestimmte ganze teilerfremde Zahlen ${}(u,v)$ mit ${}v>0$ und ${}a\in \mathbb {Z}$ und mit

$x=a(v^{2}-u^{2}),\,y=a(2uv),\,z=a(u^{2}+v^{2}).$

Das pythagoreische Tripel ist primitiv genau dann, wenn ${}a$ eine Einheit ist und ${}u$ und ${}v$ nicht beide ungerade sind.

Beweis

Es sei ${}(x,y,z)$ ein pythagoreisches Tripel. Der Fall ${}z=0$ ist ausgeschlossen. Dann ist ${}\left({\frac {x}{z}},\,{\frac {y}{z}}\right)$ ein Punkt auf dem Einheitskreis mit rationalen Koordinaten. Nach Satz 10.4 gibt es, da ${}z\neq -x$ vorausgesetzt wurde, eine eindeutig bestimmte rationale Zahl ${}t$ mit

{}\left({\frac {1-t^{2}}{1+t^{2}}},\,{\frac {2t}{1+t^{2}}}\right)=\left({\frac {x}{z}},\,{\frac {y}{z}}\right)\,.

Dann gibt es eine rationale Zahl ${}q\neq 0$ mit

x=q(1-t^{2}),\,y=q2t,\,z=q(1+t^{2}).

Sei ${}t={\frac {u}{v}}$ mit ganzen teilerfremden Zahlen ${}u,v$ , ${}v>0$ . Wir ersetzen ${}q$ durch

{}{\tilde {q}}={\frac {q}{v^{2}}}\,

und haben dann

x={\tilde {q}}(v^{2}-u^{2}),\,y={\tilde {q}}2uv,\,z={\tilde {q}}(u^{2}+v^{2}).

Da ${}u$ und ${}v$ teilerfremd sind, sind auch ${}u,v,v^{2}-u^{2}$ paarweise teilerfremd. Ein Primteiler des Nenners von ${}{\tilde {q}}$ teilt ${}2uv$ und ${}v^{2}-u^{2}$ . Daher kommt nur ${}2$ in Frage. In diesem Fall wären aber ${}v^{2}-u^{2}$ und ${}u^{2}+v^{2}$ gerade, und ${}u$ und ${}v$ wären beide ungerade. Dann wäre aber ${}y={\tilde {q}}2uv$ ungerade im Widerspruch zur Voraussetzung. Also ist ${}{\tilde {q}}$ eine ganze Zahl.

Wenn das pythagoreische Tripel primitiv ist, so muss in dieser Darstellung ${}{\tilde {q}}=1$ oder ${}-1$ sein. Außerdem können dann ${}u$ und ${}v$ nicht beide ungerade sein, sonst wäre ${}2$ ein gemeinsamer Teiler des Tripels. Wenn umgekehrt diese Bedingungen erfüllt sind, so ist das Tripel primitiv.

\Box

${}u$	${}v$	${}x=v^{2}-u^{2}$	${}y=2uv$	${}z=u^{2}+v^{2}$	${}x^{2}+y^{2}=z^{2}$
${}1$	${}2$	${}3$	${}4$	${}5$	${}9+16=25$
${}2$	${}3$	${}5$	${}12$	${}13$	${}25+144=169$
${}1$	${}4$	${}15$	${}8$	${}17$	${}225+64=289$
${}3$	${}4$	${}7$	${}24$	${}25$	${}49+576=625$
${}2$	${}5$	${}21$	${}20$	${}29$	${}441+400=841$
${}1$	${}6$	${}35$	${}12$	${}37$	${}1225+144=1369$
${}4$	${}5$	${}9$	${}40$	${}41$	${}81+1600=1681$
${}2$	${}7$	${}45$	${}28$	${}53$	${}2025+784=2809$
${}5$	${}6$	${}11$	${}60$	${}61$	${}121+3600=3721$
${}4$	${}7$	${}33$	${}56$	${}65$	${}1089+3136=4225$
${}1$	${}8$	${}63$	${}16$	${}65$	${}3969+256=4225$
${}3$	${}8$	${}55$	${}48$	${}73$	${}3025+2304=5329$
${}6$	${}7$	${}13$	${}84$	${}85$	${}169+7056=7225$
${}2$	${}9$	${}77$	${}36$	${}85$	${}5929+1296=7225$
${}5$	${}8$	${}39$	${}80$	${}89$	${}1521+6400=7921$
${}4$	${}9$	${}65$	${}72$	${}97$	${}4225+5184=9409$

Beispiel

Wenn man einen rationalen Punkt auf dem Einheitskreis sucht, der möglichst nahe an dem irrationalen Punkt ${}\left({\frac {1}{\sqrt {2}}},\,{\frac {1}{\sqrt {2}}}\right)$ liegen soll, so kann man

{}t={\frac {\frac {1}{\sqrt {2}}}{1+{\frac {1}{\sqrt {2}}}}}={\frac {1}{1+{\sqrt {2}}}}=0,414213...\,

berechnen. Die rationale Approximation

{}t'={\frac {414213}{1000000}}\,

führt zum rationalen Punkt

\left({\frac {828427590631}{1171572409369}},\,{\frac {828426000000}{1171572409369}}\right)

auf dem Einheitskreis und zum pythagoreischen Tripel

{}{\begin{aligned}x&=v^{2}-u^{2}\\&=1000000^{2}-414213^{2}\\&=1000000000000-171572409369\\&=828427590631,\end{aligned}}

{}y=2\cdot 414213\cdot 1000000=828426000000\,

und

{}{\begin{aligned}z&=u^{2}+v^{2}\\&=414213^{2}+1000000^{2}\\&=1171572409369.\end{aligned}}

In der Tat ist

{}{\begin{aligned}828427590631^{2}+828426000000^{2}&=686292272918683718978161+686289637476000000000000\\&=1372581910394683718978161\\&=1171572409369^{2},\,\end{aligned}}

wie man unmittelbar nachrechnet.

Höhere Fermat-Gleichungen

Die folgende Aussage heißt Satz von Euler.

Satz

Die diophantische Gleichung

{}x^{4}+y^{4}=z^{2}\,

hat keine ganzzahlige nichttriviale Lösung.

Beweis

Es sei ${}(x,y,z)$ eine nichttriviale Lösung, d.h. alle Einträge sind ${}\neq 0$ . Wir können annehmen, dass alle Einträge sogar positiv sind. Wenn es eine solche Lösung gibt, dann gibt es auch eine nichttriviale Lösung mit minimalem positiven ${}z$ (unter allen nichttrivialen Lösungen). Wir zeigen, dass es dann eine Lösung mit kleinerem positiven ${}z_{1}$ gibt, was einen Widerspruch bedeutet.

Wegen der Minimalität ist ${}(x,y,z)$ primitiv, die Einträge sind also (sogar paarweise) teilerfremd. Wir können ${}x$ als ungerade annehmen. Es ist dann

(x^{2},y^{2},z)

ein primitives pythagoreisches Tripel. Daher gibt es nach Satz 10.6 teilerfremde natürliche Zahlen ${}(u,v)$ mit

x^{2}=u^{2}-v^{2},\,y^{2}=2uv,\,z=u^{2}+v^{2}

und mit ${}u+v$ ungerade. Betrachtung der ersten Gleichung modulo ${}4$ zeigt, dass ${}u$ ungerade sein muss (und ${}v$ gerade). Die erste Gleichung

{}u^{2}=x^{2}+v^{2}\,

ist selbst ein primitives pythagoreisches Tripel. Es gibt als erneut teilerfremde natürliche Zahlen ${}(r,s)$ mit

x=r^{2}-s^{2},\,v=2rs,\,u=r^{2}+s^{2}

( ${}x$ ist ungerade, ${}v$ gerade) mit ${}r+s$ ist ungerade. Somit sind ${}r,s,r^{2}+s^{2}=u$ paarweise teilerfremd. Aus

{}y^{2}=2uv=4(r^{2}+s^{2})rs\,

folgt

{}\left({\frac {y}{2}}\right)^{2}=(r^{2}+s^{2})rs\,

und aus der Teilerfremdheit der Faktoren folgt, dass die einzelnen Faktoren hier selbst Quadrate sind, also

r=x_{1}^{2},\,s=y_{1}^{2},\,r^{2}+s^{2}=z_{1}^{2}.

Damit ist

{}z_{1}^{2}=r^{2}+s^{2}=x_{1}^{4}+y_{1}^{4}\,

eine neue nichttriviale Lösung der ursprünglichen Gleichung. Wegen

{}z_{1}\leq z_{1}^{2}=r^{2}+s^{2}=u<u^{2}+v^{2}=z\,

widerspricht dies der Minimalität von ${}z$ .

\Box

Korollar

Die Fermat-Quartik

{}x^{4}+y^{4}=z^{4}\,

besitzt keine ganzzahlige nichttriviale Lösung.

Beweis

Dies folgt sofort aus dem Satz von Euler.

\Box

Generell nennt man Gleichungen der Form

{}x^{n}+y^{n}=z^{n}\,

Fermat-Gleichungen. Die berühmte Vermutung von Fermat, der sogenannte „Große Fermat“, besagt, dass es für ${}n\geq 3$ keine nicht-trivialen Lösungen gibt. Dies haben wir soeben für ${}n=4$ bewiesen. Der Fall ${}n=3$ (Fermat-Kubiken) lässt sich ebenfalls noch einigermaßen elementar bestätigen (Euler) und hat mit den Eisenstein-Zahlen zu tun. Nach rund 350 Jahren wurde der Große Fermat schließlich 1995 von Andrew Wiles bewiesen.

Satz

Die diophantische Gleichung

{}x^{n}+y^{n}=z^{n}\,

besitzt für kein ${}n\geq 3$ eine ganzzahlige nichttriviale Lösung.

Beweis

Der Beweis für diese Aussage geht bei Weitem über den Inhalt einer Vorlesung über elementare oder algebraische Zahlentheorie hinaus.

\Box

<< | Kurs:Zahlentheorie (Osnabrück 2016-2017) | >>

PDF-Version dieser Vorlesung

Arbeitsblatt zur Vorlesung (PDF)