Kurs:Analysis (Osnabrück 2014-2016)/Teil III/Vorlesung 77

Der Tangentialraum einer differenzierbaren Mannigfaltigkeit

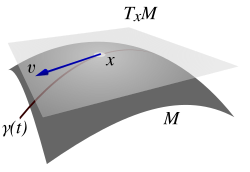
Für eine offene Menge ${}V\subseteq \mathbb {R} ^{n}$ und einen Punkt ${}P\in V$ repräsentiert der umgebende reelle Vektorraum ${}\mathbb {R} ^{n}$ die Menge aller möglichen Richtungen in diesem Punkt. Man kann den Vektor ${}v\in \mathbb {R} ^{n}$ mit dem Weg

$I\longrightarrow V,\,t\longmapsto P+tv,$

identifizieren, wobei ${}0\in I$ ein reelles Intervall derart ist, dass das Bild der Abbildung in ${}V$ liegt. Diesen Vektorraum nennt man den Tangentialraum im Punkt ${}P$ an ${}V$.

Für die Faser einer differenzierbaren Abbildung ${}\varphi \colon G\rightarrow \mathbb {R} ^{m}$, ${}G\subseteq \mathbb {R} ^{n}$ offen, in einem regulären Punkt ${}P\in G$ haben wir den Tangentialraum an die Faser durch ${}P$ als Kern des totalen Differentials ${}\left(D\varphi \right)_{P}\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}$ definiert. Dadurch war der Tangentialraum ein ${}(n-m)$-dimensionaler Untervektorraum des umgebenden Vektorraums ${}\mathbb {R} ^{n}$. Für unseren abstrakten Mannigfaltigkeitsbegriff gibt es einen solchen umgebenden Vektorraum nicht, in dem sich alles abspielt. Dennoch können wir auch für eine Mannigfaltigkeit in jedem Punkt einen Tangentialraum erklären. Dieser wird ein Vektorraum sein (dessen Dimension gleich der Dimension der Mannigfaltigkeit ist), und zu einer differenzierbaren Abbildung zwischen zwei Mannigfaltigkeiten wird das totale Differential in jedem Punkt eine lineare Abbildung zwischen den Tangentialräumen sein.

Wenn man für einen Punkt ${}P\in M$ einer differenzierbaren Mannigfaltigkeit ${}M$ eine offene Umgebung ${}P\in U\subseteq M$ und eine Karte

$\alpha \colon U\longrightarrow V$

mit ${}V\subseteq \mathbb {R} ^{k}$ heranzieht, so liegt es nahe, diesen ${}\mathbb {R} ^{k}$ als Tangentialraum zu betrachten. In der Tat wird es eine solche Isomorphie geben, doch als Definition ist dieser Ansatz wegen der Abhängigkeit von der gewählten Karte unbrauchbar. Stattdessen arbeiten wir mit Äquivalenzklassen von differenzierbaren Kurven.

Definition

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit und ${}P\in M$ ein Punkt. Es seien

$\gamma _{1}\colon I_{1}\longrightarrow M$

und

$\gamma _{2}\colon I_{2}\longrightarrow M$

zwei auf offenen Intervallen ${}0\in I_{1},I_{2}\subseteq \mathbb {R}$ definierte differenzierbare Kurven mit ${}\gamma _{1}(0)=P=\gamma _{2}(0)$. Dann heißen ${}\gamma _{1}$ und ${}\gamma _{2}$ tangential äquivalent in ${}P$, wenn es eine offene Umgebung ${}P\in U$ und eine Karte

$\alpha \colon U\longrightarrow V$

mit ${}V\subseteq \mathbb {R} ^{n}$ derart gibt, dass

${}{\left(\alpha \circ {\left(\gamma _{1}{|}_{\gamma _{1}^{-1}(U)}\right)}\right)}'(0)={\left(\alpha \circ {\left(\gamma _{2}{|}_{\gamma _{2}^{-1}(U)}\right)}\right)}'(0)\,$

gilt.

Wir brauchen einige einfache Lemmata, um nachzuweisen, dass es sich hierbei um einen sinnvollen Begriff handelt.

Lemma

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit und ${}P\in M$ ein Punkt. Es seien

$\gamma _{1}\colon I_{1}\longrightarrow M$

und

$\gamma _{2}\colon I_{2}\longrightarrow M$

zwei auf offenen Intervallen ${}0\in I_{1},I_{2}\subseteq \mathbb {R}$ definierte differenzierbare Kurven mit ${}\gamma _{1}(0)=P=\gamma _{2}(0)$.

Dann sind ${}\gamma _{1}$ und ${}\gamma _{2}$ genau dann tangential äquivalent in ${}P$, wenn für jede Karte

$\alpha \colon U\longrightarrow V$

mit ${}P\in U$ und ${}V\subseteq \mathbb {R} ^{n}$ die Gleichheit

${}{\left(\alpha \circ {\left(\gamma _{1}{|}_{\gamma _{1}^{-1}(U)}\right)}\right)}'(0)={\left(\alpha \circ {\left(\gamma _{2}{|}_{\gamma _{2}^{-1}(U)}\right)}\right)}'(0)\,$

gilt.

Beweis

Für eine differenzierbare Kurve

$\gamma \colon I\longrightarrow M$

mit ${}0\in I$ und ${}\gamma (0)=P$ und eine Karte

$\alpha \colon U\longrightarrow V$

(mit ${}P\in U$ und ${}V\subseteq \mathbb {R} ^{n}$) ändert sich der Ausdruck

${\left(\alpha \circ {\left(\gamma {|}_{\gamma ^{-1}(U)}\right)}\right)}'(0)$

nicht, wenn man zu einem kleineren offenen Intervall ${}0\in I'\subseteq I$ und einer kleineren offenen Menge ${}P\in U'\subseteq U$ (mit der induzierten Karte) übergeht. Wir können also davon ausgehen, dass ${}\gamma _{1}$ und ${}\gamma _{2}$ auf dem gleichen Intervall definiert sind und ihre Bilder in ${}U$ liegen, und dass es für dieses ${}U$ zwei Karten

$\alpha _{1}\colon U\longrightarrow V_{1}$

und

$\alpha _{2}\colon U\longrightarrow V_{2}$

gibt. Dann folgt aus

${}(\alpha _{1}\circ \gamma _{1})'(0)=(\alpha _{1}\circ \gamma _{2})'(0)\,$

nach der Kettenregel unter Verwendung der Differenzierbarkeit der Übergangsabbildung ${}\alpha _{2}\circ \alpha _{1}^{-1}$ sofort

${}{\begin{aligned}{\left(\alpha _{2}\circ \gamma _{1}\right)}'(0)&={\left({\left(\alpha _{2}\circ \alpha _{1}^{-1}\right)}\circ {\left(\alpha _{1}\circ \gamma _{1}\right)}\right)}'(0)\\&={\left(D\left(\alpha _{2}\circ \alpha _{1}^{-1}\right)\right)}_{\alpha _{1}(P)}{\left({\left(\alpha _{1}\circ \gamma _{1}\right)}'(0)\right)}\\&={\left(D\left(\alpha _{2}\circ \alpha _{1}^{-1}\right)\right)}_{\alpha _{1}(P)}{\left({\left(\alpha _{1}\circ \gamma _{2}\right)}'(0)\right)}\\&={\left(\alpha _{2}\circ \gamma _{2}\right)}'(0).\end{aligned}}$

$\Box$

Lemma

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit und ${}P\in M$ ein Punkt.

Dann ist die tangentiale Äquivalenz von differenzierbaren Kurven durch ${}P$ eine Äquivalenzrelation.

Beweis

Die Reflexiviät und die Symmetrie der Relation sind unmittelbar klar. Zum Nachweis der Transitivität seien drei differenzierbare Kurven

$\gamma _{1},\gamma _{2},\gamma _{3}\colon I\longrightarrow M$

gegeben, wobei wir sofort annehmen dürfen, dass sie auf dem gleichen offenen Intervall ${}0\in I\subseteq \mathbb {R}$ definiert sind. Es seien ${}P\in U_{1},U_{2}$ offene Mengen, mit denen man die tangentiale Gleichheit von ${}\gamma _{1}$ und ${}\gamma _{2}$ bzw. von ${}\gamma _{2}$ und ${}\gamma _{3}$ nachweisen kann. Dann kann man nach Lemma 77.2 mit ${}U=U_{1}\cap U_{2}$ die tangentiale Gleichheit von ${}\gamma _{1}$ und ${}\gamma _{3}$ nachweisen.

$\Box$

Aufgrund dieses Lemmas ist die folgende Definition sinnvoll.

Definition

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit und ${}P\in M$ ein Punkt. Unter einem Tangentialvektor an ${}P$ versteht man eine Äquivalenzklasse von tangential äquivalenten differenzierbaren Kurven durch ${}P$. Die Menge dieser Tangentialvektoren wird mit

$T_{P}M$

bezeichnet.

Lemma

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit, ${}P\in M$ ein Punkt, ${}P\in U=M$ offen und

$\alpha \colon U\longrightarrow V$

eine Karte. Dann gelten folgende Aussagen.

1. Die Abbildung

   $T_{p}M\longrightarrow \mathbb {R} ^{n},\,[\gamma ]\longmapsto {\left(\alpha \circ \gamma {|}_{\gamma ^{-1}(U)}\right)}'(0),$

   ist eine wohldefinierte Bijektion.

2. Die durch diese Abbildung auf ${}T_{p}M$ definierte Vektorraumstruktur ist unabhängig von der gewählten Karte.

Beweis

(1). Die Wohldefiniertheit der Abbildung ist wegen Lemma 77.2 klar. Die Injektivität folgt unmittelbar aus der Definition 77.1. Zur Surjektivität sei ${}v\in \mathbb {R} ^{n}$. Wir betrachten die affin-lineare Kurve

$\theta \colon \mathbb {R} \longrightarrow \mathbb {R} ^{n},\,t\longmapsto \theta (t)=\alpha (P)+tv,$

dessen Ableitung in ${}0$ gerade ${}v$ ist. Wir schränken diese Kurve auf ein Intervall ${}0\in I\subseteq \mathbb {R}$ derart ein, dass ${}\theta (I)\subseteq V$ ist und betrachten

$\gamma =\alpha ^{-1}\circ \theta \colon I\longrightarrow M.$

Für diese Kurve gilt

${}\gamma (0)={\left(\alpha ^{-1}\circ \theta \right)}(0)=\alpha ^{-1}(\theta (0))=\alpha ^{-1}(\alpha (P))=P\,$

und

${}{\left(\alpha \circ \gamma \right)}'(0)={\left(\alpha \circ {\left(\alpha ^{-1}\circ \theta \right)}\right)}'(0)=\theta '(0)=v\,.$

(2). Durch Übergang zu kleineren offenen Mengen können wir annehmen, dass zwei Karten

$\alpha _{1}\colon U\longrightarrow V_{1}$

und

$\alpha _{2}\colon U\longrightarrow V_{2}$

vorliegen. Die Übergangsabbildung

$\alpha _{2}\circ \alpha _{1}^{-1}\colon V_{1}\longrightarrow V_{2}$

ist ein ${}C^{1}$- Diffeomorphismus und für ihr totales Differential in ${}\alpha _{1}(P)$ gilt nach der Kettenregel die Beziehung

${}{\left(D(\alpha _{2}\circ \alpha _{1}^{-1})\right)}_{\alpha _{1}(P)}{\left((\alpha _{1}\circ \gamma )'(0)\right)}=(\alpha _{2}\circ \gamma )'(0)\,.$

Das bedeutet, dass das Diagramm

${\begin{matrix}T_{P}M&{\stackrel {}{\longrightarrow }}&\mathbb {R} ^{n}&\\&\searrow &\downarrow &\\&&\mathbb {R} ^{n}&\!\!\!\!\!\!\!\!,\\\end{matrix}}$

wobei vertikal das totale Differential zu ${}\alpha _{2}\circ \alpha _{1}^{-1}$ steht, kommutiert. Da das totale Differential eine lineare Abbildung ist, die in der gegebenen Situation bijektiv ist, macht es keinen Unterschied, ob man die Addition und die Skalarmultiplikation auf ${}T_{P}M$ unter Bezug auf die obere oder die untere horizontale Abbildung definiert.

$\Box$

Definition

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit und ${}P\in M$ ein Punkt. Unter dem Tangentialraum an ${}P$, geschrieben ${}T_{P}M$, versteht man die Menge der Tangentialvektoren an ${}P$ versehen mit der durch eine beliebige Karte gegebenen reellen Vektorraumstruktur.

Die Dimension des Tangentialraumes stimmt mit der Dimension der Mannigfaltigkeit überein. Jede Karte induziert einen Isomorphismus zwischen ${}T_{P}M$ und dem ${}\mathbb {R} ^{n}$, aber diese Isomorphismen hängen von der gewählten Karte ab. Insbesondere gibt es auf dem Tangentialraum keine Standardbasis.

Definition

Es sei ${}M$ eine differenzierbare Mannigfaltigkeit und ${}P\in M$ ein Punkt. Den Dualraum des Tangentialraumes

${}T_{P}M$ an ${}P$ nennt man den Kotangentialraum an ${}P$. Er wird mit

$T_{P}^{*}M$

bezeichnet.

Lemma

Es seien ${}M$ und ${}N$ differenzierbare Mannigfaltigkeiten und es sei

$\varphi \colon M\longrightarrow N$

eine differenzierbare Abbildung. Es sei ${}P\in M$ und ${}Q=\varphi (P)$ und es seien

$\gamma _{1},\gamma _{2}\colon I\longrightarrow M$

zwei differenzierbare Kurven mit einem offenen Intervall ${}0\in I$ und ${}\gamma _{1}(0)=\gamma _{2}(0)=P$. Es seien ${}\gamma _{1}$ und ${}\gamma _{2}$ im Punkt ${}P$ tangential äquivalent.

Dann sind auch die Verknüpfungen ${}\varphi \circ \gamma _{1}$ und ${}\varphi \circ \gamma _{2}$ tangential äquivalent in ${}Q$.

Beweis

Siehe Aufgabe 77.3.

$\Box$

Aufgrund dieses Lemmas ist der folgende Begriff wohldefiniert.

Definition

Es seien ${}M$ und ${}N$ differenzierbare Mannigfaltigkeiten und es sei

$\varphi \colon M\longrightarrow N$

eine differenzierbare Abbildung. Es sei ${}P\in M$ und ${}Q=\varphi (P)$. Dann nennt man die Abbildung

$T_{P}M\longrightarrow T_{\varphi (P)}N,\,[\gamma ]\longmapsto [\varphi \circ \gamma ],$

die zugehörige Tangentialabbildung im Punkt ${}P$. Sie wird mit ${}T_{P}(\varphi )$ bezeichnet.

Lemma

Es seien ${}M$ und ${}N$ differenzierbare Mannigfaltigkeiten und es sei

$\varphi \colon M\longrightarrow N$

eine differenzierbare Abbildung. Es sei ${}P\in M$ , ${}Q=\varphi (P)$ und es sei

$T_{P}(\varphi )\colon T_{P}M\longrightarrow T_{Q}N$

die zugehörige Tangentialabbildung. Dann gelten folgende Aussagen.

1. Wenn ${}M\subseteq \mathbb {R} ^{m}$ und ${}N\subseteq \mathbb {R} ^{n}$ offene Teilmengen sind und die Tangentialräume mit den umgebenden euklidischen Räumen identifiziert werden, so ist die Tangentialabbildung gleich dem totalen Differential ${}\left(D\varphi \right)_{P}$.
2. Wenn

   $\alpha \colon U\longrightarrow V$

   mit ${}P\in U$ und ${}V\subseteq \mathbb {R} ^{m}$ und

   $\beta \colon U'\longrightarrow W$

   mit ${}Q\in U'$ und ${}W\subseteq \mathbb {R} ^{n}$ Karten sind, so ist das Diagramm

   ${\begin{matrix}T_{p}M&{\stackrel {T_{P}\varphi }{\longrightarrow }}&T_{Q}N&\\\downarrow &&\downarrow &\\\mathbb {R} ^{m}&{\stackrel {\left(D{\left(\beta \circ \varphi \circ \alpha ^{-1}\right)}\right)_{\alpha (P)}}{\longrightarrow }}&\mathbb {R} ^{n}&\!\!\!\!\!\\\end{matrix}}$

   kommutativ, wobei die vertikalen Abbildungen durch die Isomorphismen ${}[\gamma ]\mapsto (\alpha \circ \gamma )'(0)$ bzw. ${}[\gamma ]\mapsto (\beta \circ \gamma )'(0)$ gegeben sind.

3. ${}T_{P}(\varphi )$ ist ${}\mathbb {R}$- linear.
4. Wenn ${}L$ eine weitere Mannigfaltigkeit, ${}R\in L$ und

   $\psi \colon L\longrightarrow M$

   eine weitere differenzierbare Abbildung mit ${}\psi (R)=P$ ist, so gilt

   ${}T_{R}(\varphi \circ \psi )=T_{P}(\varphi )\circ T_{R}(\psi )\,.$

5. Wenn ${}\varphi$ ein Diffeomorphismus ist, dann ist ${}T_{P}(\varphi )$ ein Isomorphismus.
6. Für eine differenzierbare Kurve

   $\gamma \colon I\longrightarrow M$

   mit einem offenen Intervall ${}I\subseteq \mathbb {R}$, ${}0\in I$ und ${}\gamma (0)=P$ gilt im Tangentialraum ${}T_{P}M$ die Gleichheit

   ${}[\gamma ]=(T_{0}(\gamma ))(1)\,.$

Beweis

(1). Jeder Tangentialvektor wird repräsentiert durch einen affin-linearen Weg ${}t\mapsto \gamma (t)=P+tv$ mit einem Vektor ${}v\in \mathbb {R} ^{m}$, sodass wir zwischen diesen Vektoren und den durch sie definierten Tangentialvektoren hin- und herwechseln können. Für den zusammengesetzten Weg ${}\varphi \circ \gamma$ gilt nach der Kettenregel

${}(T_{P}\varphi )([\gamma ])=[\varphi \circ \gamma ]=(\varphi \circ \gamma )'(0)=(D\varphi )_{P}\left({\left(D\gamma \right)}_{0}{\left(1\right)}\right)={\left(D\varphi \right)}_{P}{\left(v\right)}\,.$

(2). Die Kettenregel angewendet auf (wobei man ${}I$ und ${}V$ durch kleinere offene Mengen ersetzen muss)

$I{\stackrel {\alpha \circ \gamma }{\longrightarrow }}V{\stackrel {\beta \circ \varphi \circ \alpha ^{-1}}{\longrightarrow }}W$

liefert

${}{\left(D\left(\beta \circ \varphi \circ \alpha ^{-1}\right)\right)}_{\alpha (P)}{\left((\alpha \circ \gamma )'(0)\right)}=(\beta \circ (\varphi \circ \gamma ))'(0)\,,$

was gerade die Kommutativität des Diagramms ist.
(3). Die Aussage folgt aus (2) und der Linearität des totalen Differentials.
(4). Durch Übergang zu Karten folgt dies aus (2) und der Kettenregel.
(5) folgt aus (4) angewendet auf die Umkehrabbildung ${}\varphi ^{-1}$.
(6). Das Element ${}1\in \mathbb {R}$ ist als Tangentenvektor an einem Punkt ${}a\in I$ als der Weg ${}s\mapsto a+s$ zu interpretieren. Bei ${}a=0$ ist dies der identische Weg. Daher ist

${}(T_{0}(\gamma ))(1)=(T_{0}(\gamma ))(\operatorname {Id} )=[\gamma \circ \operatorname {Id} ]=[\gamma ]\,.$

$\Box$

Definition

Es seien ${}M$ und ${}N$ differenzierbare Mannigfaltigkeiten und

$\varphi \colon M\longrightarrow N$

eine differenzierbare Abbildung. Es sei ${}P\in M$ und ${}Q=\varphi (P)$. Dann nennt man die zur Tangentialabbildung

$T_{P}(\varphi )\colon T_{P}M\longrightarrow T_{Q}N$

duale Abbildung

$T_{Q}^{*}N\longrightarrow T_{P}^{*}M,\,h\longmapsto h\circ T_{P}(\varphi ),$

die Kotangentialabbildung im Punkt ${}P$. Sie wird mit ${}T_{P}^{*}(\varphi )$ bezeichnet.

Ausgeschrieben handelt es sich dabei um die Abbildung

$T_{Q}^{*}N\longrightarrow T_{P}^{*}M,\,h\longmapsto ([\gamma ]\mapsto h([\varphi \circ \gamma ])).$

Definition

Es seien ${}L$ und ${}M$ differenzierbare Mannigfaltigkeiten und sei

$\varphi \colon L\longrightarrow M$

eine differenzierbare Abbildung. Dann heißt ${}\varphi$ im Punkt ${}Q\in L$ regulär (und ${}Q$ ein regulärer Punkt für ${}\varphi$), wenn die Tangentialabbildung

$T_{Q}(\varphi )\colon T_{Q}L\longrightarrow T_{\varphi (Q)}M$

im Punkt ${}Q$ maximalen Rang besitzt.

Diese Definition verallgemeinert die entsprechende Definition 52.2 von euklidischen Teilmengen auf Mannigfaltigkeiten. Sie bedeutet einfach, dass bei ${}\operatorname {dim} (L)\geq \operatorname {dim} (M)$ die Tangentialabbildung in ${}Q$ surjektiv sein muss und bei ${}\operatorname {dim} (L)\leq \operatorname {dim} (M)$ injektiv sein muss.

<< | Kurs:Analysis (Osnabrück 2014-2016)/Teil III | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)