Kurs:Einführung in die Algebra (Osnabrück 2009)/Vorlesung 16

Polynomringe

Definition

Der Polynomring über einem kommutativen Ring ${}R$ besteht aus allen Polynomen

$P=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{n}X^{n}$

mit ${}a_{i}\in R,\,i=0,\ldots ,n,\,n\in \mathbb {N}$,

und mit komponentenweiser Addition und einer Multiplikation, die durch distributive Fortsetzung der Regel

${}X^{n}\cdot X^{m}:=X^{n+m}\,$

definiert ist.

Ein Polynom

${}P=\sum _{i=0}^{n}a_{i}X^{i}=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{n}X^{n}\,$

ist formal gesehen nichts anderes als das Tupel ${}(a_{0},a_{1},\ldots ,a_{n})$, die die Koeffizienten des Polynoms heißen. Der Ring ${}R$ heißt in diesem Zusammenhang der Grundring des Polynomrings. Aufgrund der komponentenweisen Definition der Addition liegt unmittelbar eine Gruppe vor, mit dem Nullpolynom (bei dem alle Koeffizienten null sind) als neutralem Element. Zwei Polynome sind genau dann gleich, wenn sie in allen ihren Koeffizienten übereinstimmen. Die Polynome mit ${}a_{i}=0$ für alle ${}i\geq 1$ heißen konstante Polynome, man schreibt sie einfach als ${}a_{0}$.

Die für ein einfaches Tupel zunächst ungewöhnliche Schreibweise deutet in suggestiver Weise an, wie die Multiplikation aussehen soll, das Produkt ${}X^{i}X^{j}$ ist nämlich durch die Addition der Exponenten gegeben. Dabei nennt man ${}X$ die Variable des Polynomrings. Für beliebige Polynome ergibt sich die Multiplikation aus dieser einfachen Multiplikationsbedingung durch distributive Fortsetzung gemäß der Vorschrift, „alles mit allem“ zu multiplizieren. Die Multiplikation ist also explizit durch folgende Regel gegeben:

${\left(\sum _{i=0}^{n}a_{i}X^{i}\right)}\cdot {\left(\sum _{j=0}^{m}b_{j}X^{j}\right)}=\sum _{k=0}^{n+m}c_{k}X^{k}{\text{ mit }}c_{k}=\sum _{r=0}^{k}a_{r}b_{k-r}.$

Lemma

Es sei ${}R$ ein kommutativer Ring und sei ${}R[X]$ der Polynomring über ${}R$. Dann gelten folgende Aussagen.

1. ${}R$ ist ein Unterring von ${}R[X]$.
2. ${}R$ ist genau dann ein Integritätsbereich, wenn ${}R[X]$ ein Integritätsbereich ist.

Beweis

1. Ein Element ${}r\in R$ wird als konstantes Polynom aufgefasst, wobei es egal ist, ob man Addition und Multiplikation in ${}R$ oder in ${}R[X]$ ausführt.
2. Wenn ${}R[X]$ integer ist, so überträgt sich dies sofort auf den Unterring ${}R$. Es sei also ${}R$ ein Integritätsbereich und seien ${}P=\sum _{i=0}^{n}a_{i}X^{i}$ und ${}Q=\sum _{j=0}^{m}b_{j}X^{j}$ zwei von null verschiedene Polynome. Wir können annehmen, dass ${}a_{n}$ und ${}b_{m}$ von null verschieden sind. Dann ist ${}a_{n}b_{m}\neq 0$ und dies ist der Leitkoeffizient des Produktes ${}PQ$, das damit nicht null sein kann.

$\Box$

Der Einsetzungshomomorphismus

Satz

Es sei ${}R$ ein kommutativer Ring und sei ${}R[X]$ der Polynomring über ${}R$. Es sei ${}A$ ein weiterer kommutativer Ring und es sei ${}\varphi \colon R\rightarrow A$ ein Ringhomomorphismus und ${}a\in A$ ein Element.

Dann gibt es einen eindeutig bestimmten Ringhomomorphismus

$\psi \colon R[X]\longrightarrow A$

mit ${}\psi (X)=a$ und mit ${}\psi \circ i=\varphi$, wobei ${}i\colon R\rightarrow R[X]$ die kanonische Einbettung ist.

Dabei geht das Polynom ${}P=\sum _{j=0}^{n}c_{j}X^{j}$ auf ${}\sum _{j=0}^{n}\varphi (c_{j})a^{j}$.

Beweis

Bei einem Ringhomomorphismus

$\psi \colon R[X]\longrightarrow A$

mit ${}\psi \circ i=\varphi$. müssen die Konstanten ${}c\in R$ auf ${}\varphi (c)$ und ${}X$ auf ${}a$ gehen. Daher muss ${}X^{j}$ auf ${}a^{j}$ gehen. Da Summen respektiert werden, kann es nur einen Ringhomorphismus geben, der die im Zusatz angegebene Gestalt haben muss. Es ist also zu zeigen, dass durch diese Vorschrift wirklich ein Ringhomomorphismus definiert ist. Dies folgt aber direkt aus dem Distributivgesetz.

$\Box$

Den in diesem Satz konstruierten Ringhomomorphismus nennt man den Einsetzungshomomorphismus.

Korollar

Es sei ${}R$ ein kommutativer Ring und sei ${}R[X]$ der Polynomring über ${}R$. Es sei ${}Y=aX+b$, wobei ${}a$ eine Einheit in ${}R$ sei.

Dann gibt es einen Ringisomorphismus

$R[X]\longrightarrow R[X],\,X\longmapsto aX+b.$

Beweis

Die Einsetzungshomomorphismen zu ${}X\mapsto aX+b$ und ${}X\mapsto a^{-1}X-a^{-1}b$ definieren aufgrund von Korollar 14.4 jeweils einen Ringhomomorphismus ${}\psi$ und ${}\varphi$ von ${}R[X]$ nach ${}R[X]$, die wir hintereinander schalten:

$R[X]{\stackrel {\psi }{\longrightarrow }}R[X]{\stackrel {\varphi }{\longrightarrow }}R[X].$

Bei diesem Ringhomomorphismus bleiben die Elemente aus ${}R$ unverändert, und die Variable ${}X$ wird insgesamt auf

${}a(a^{-1}X-a^{-1}b)+b=aa^{-1}X-aa^{-1}b+b=X\,$

geschickt. Daher muss die Verknüpfung aufgrund der Eindeutigkeit in Korollar 14.4 die Identität sein. Dies gilt auch für die Hintereinanderschaltung in umgekehrter Reihenfolge, sodass ein Isomorphismus vorliegt.

$\Box$

Korollar

Es sei ${}R$ ein kommutativer Ring und sei ${}S\subseteq R$ ein Unterring.

Dann ist auch ${}S[X]$ ein Unterring von ${}R[X]$.

Beweis

Wir betrachten den zusammengesetzten Ringhomomorphismus

$S\longrightarrow R\longrightarrow R[X].$

Dann liefert der zu ${}X\mapsto X$ nach Korollar 14.4 gehörige Einsetzungshomomorphismus

$S[X]\longrightarrow R[X]$

die gewünschte Abbildung.

$\Box$

Die vorstehende Aussage bedeutet einfach, dass man ein Polynom mit Koeffizienten aus ${}S$ direkt auch als Polynom mit Koeffizienten aus ${}R$ auffassen kann. So ist ein Polynom mit ganzzahligen Koeffizienten insbesondere auch ein Polynom mit rationalen Koeffizienten und mit reellen Koeffizienten. Die Addition und die Multiplikation von zwei Polynomen hängt nicht davon ab, ob man sie über einem kleineren oder einem größeren Grundring ausrechnet, so lange dieser nur alle beteiligten Koeffizienten enthält. Es gibt aber auch viele wichtige Eigenschaften, die vom Grundring abhängen, wie beispielsweise die Eigenschaft, irreduzibel zu sein.

Der Grad eines Polynoms

Definition

Der Grad eines von ${}0$ verschiedenen Polynoms

${}P=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{n}X^{n}\,$

mit ${}a_{n}\neq 0$ ist ${}n$.

In der Situation der vorstehenden Definition heißt ${}a_{n}$ der Leitkoeffizient des Polynoms. Wenn der Leitkoeffizient ${}1$ ist, so nennt man das Polynom normiert. Dem Nullpolynom wird im Allgemeinen kein Grad zugewiesen; manchmal sind gewisse Gleichungen oder Bedingungen aber auch so zu verstehen, dass dem Nullpolynom jeder Grad zugewiesen wird.

Lemma

Es sei ${}R$ ein kommutativer Ring und sei ${}R[X]$ der Polynomring über ${}R$. Dann gelten für den Grad folgende Aussagen.

1. ${}\operatorname {grad} \,(P+Q)\leq \max\{\operatorname {grad} \,(P),\,\operatorname {grad} \,(Q)\}\,.$

2. ${}\operatorname {grad} \,(P\cdot Q)\leq \operatorname {grad} \,(P)+\operatorname {grad} \,(Q)\,.$

3. Wenn ${}R$ ein Integritätsbereich ist, so gilt in (2) die Gleichheit.

Beweis

Das ist trivial.

$\Box$

Die Konstruktion von Polynomringen aus einem Grundring kann man iterieren. Aus ${}R$ kann man ${}R[X]$ machen und daraus mit einer neuen Variablen den Ring ${}(K[X])[Y]$ bilden. Für diesen Ring schreibt man auch ${}R[X,Y]$. Ein Element darin hat die Gestalt

$\sum _{i,j}a_{ij}X^{i}Y^{j}.$

Bemerkung  

Zu einem Ring ${}A$ und einer beliebigen Teilmenge ${}T\subseteq A$ kann man den von ${}T$ erzeugten Unterring betrachten. Das ist der kleinste Unterring von ${}A$, der ${}T$ umfasst; man kann ihn einfach als den Durchschnitt aller ${}T$ umfassenden Unterringe realisieren.

Häufig ist man in eine Situation interessiert, wo ${}R\subseteq A$ ein fixierter Unterring ist und eine weitere, typischerweise recht kleine Teilmenge ${}T\subseteq A$ gegeben ist. Dann wird der von ${}R$ und ${}T$ gemeinsam erzeugte Unterring von ${}A$ mit ${}R[T]$ bezeichnet. Es sei vorausgesetzt, dass ${}R$ mit allen Elementen aus ${}T$ vertauschbar ist (was bei kommutativen ${}A$ automatisch der Fall ist). Dann besteht dieser erzeugte Unterring aus allen polynomialen Ausdrücken

$\sum _{\nu }r_{\nu }t^{\nu _{1}}{\cdots }t_{k}^{\nu _{k}}$

mit ${}r_{\nu }\in R,\,t_{1},\ldots ,t_{k}\in T,\,\nu =(\nu _{1},\ldots ,\nu _{k})\in \mathbb {N} ^{k}$.

Diese Ausdrücke bilden offensichtlich den durch ${}R$ und ${}T$ erzeugten Unterring. Bei ${}T=\{x\}$ schreibt man dafür

${}R[x]={\left\{\sum _{i=0}^{n}a_{i}x^{i}\mid a_{i}\in R\right\}}\,.$

Man beachte, dass im Gegensatz zum Polynomring dabei die Darstellung eines Elementes aus ${}R[T]$ als ein polynomialer Ausdruck keineswegs eindeutig bestimmt sein muss.

Polynomringe über einem Körper

Es bestehen viele und weitreichende Parallelen zwischen dem Ring ${}\mathbb {Z}$ der ganzen Zahlen und einem Polynomring in einer Variablen über einem Körper. Grundlegend ist, dass man in beiden Situation eine Division mit Rest durchführen kann.

Satz

Es sei ${}K$ ein Körper und sei ${}K[X]$ der Polynomring über ${}K$. Es seien ${}P,T\in K[X]$ Polynome mit ${}T\neq 0$.

Dann gibt es eindeutig bestimmte Polynome ${}Q,R\in K[X]$ mit

$P=TQ+R{\text{ und mit }}\operatorname {grad} \,(R)<\operatorname {grad} \,(T){\text{ oder }}R=0.$

Beweis

Wir beweisen die Existenzaussage durch Induktion über den Grad von ${}P$. Wenn der Grad von ${}T$ größer als der Grad von ${}P$ ist, so ist ${}Q=0$ und ${}R=P$ eine Lösung, sodass wir dies nicht weiter betrachten müssen. Bei ${}\operatorname {grad} \,(P)=0$ ist nach der Vorbemerkung auch ${}\operatorname {grad} \,(TP)=0$, also ist ${}T$ ein konstantes Polynom, und damit ist (da ${}T\neq 0$ und ${}K$ ein Körper ist) ${}Q=P/T$ und ${}R=0$ eine Lösung. Es sei nun ${}\operatorname {grad} \,(P)=n$ und die Aussage für kleineren Grad schon bewiesen. Wir schreiben ${}P=a_{n}X^{n}+\cdots +a_{1}X+a_{0}$ und ${}T=b_{k}X^{k}+\cdots +b_{1}X+b_{0}$ mit ${}a_{n},b_{k}\neq 0,\,k\leq n$. Dann gilt mit ${}H={\frac {a_{n}}{b_{k}}}X^{n-k}$ die Beziehung

${}{\begin{aligned}P'&:=P-TH\\&=0X^{n}+{\left(a_{n-1}-{\frac {a_{n}}{b_{k}}}b_{k-1}\right)}X^{n-1}+\cdots +{\left(a_{n-k}-{\frac {a_{n}}{b_{k}}}b_{0}\right)}X^{n-k}+a_{n-k-1}X^{n-k-1}+\cdots +a_{0}.\end{aligned}}$

Dieses Polynom ${}P'$ hat einen Grad kleiner als ${}n$ und darauf können wir die Induktionsvoraussetzung anwenden, d.h. es gibt ${}Q'$ und ${}R'$ mit

$P'=TQ'+R'{\text{ mit }}\operatorname {grad} \,(R')<\operatorname {grad} \,(T){\text{ oder }}R'=0.$

Daraus ergibt sich insgesamt

${}P=P'+TH=TQ'+TH+R'=T(Q'+H)+R'\,,$

sodass also ${}Q=Q'+H$ und ${}R=R'$ eine Lösung ist. Zur Eindeutigkeit sei ${}P=TQ+R=TQ'+R'$ mit den angegebenen Bedingungen. Dann ist ${}T(Q-Q')=R'-R$. Da die Differenz ${}R'-R$ einen Grad kleiner als ${}\operatorname {grad} \,(T)$ besitzt, ist aufgrund der Gradeigenschaften diese Gleichung nur bei ${}R=R'$ und ${}Q=Q'$ lösbar.

$\Box$

Bemerkung  

Das in Satz 16.9 beschriebene Verfahren, um zu zwei gegebenen Polynomen ${}P$ und ${}T$ Polynome ${}Q$ und ${}R$ zu finden mit

$P=TQ+R{\text{ mit }}\operatorname {grad} \,(R)<\operatorname {grad} \,(T){\text{ oder }}R=0,$

ist konstruktiv und lässt sich rechnerisch einfach durchführen, wenn man die Arithmetik im Grundkörper ${}K$ beherrscht. Dieses Verfahren heißt Division mit Rest.

Satz

Ein Polynomring über einem Körper

ist ein Hauptidealbereich.

Beweis

Es sei ${}I$ ein von ${}0$ verschiedenes Ideal in ${}K[X]$. Betrachte die nichtleere Menge

${\left\{\operatorname {grad} \,(P)\mid P\in I,\,P\neq 0\right\}}.$

Diese Menge hat ein Minimum ${}m\in \mathbb {N}$, das von einem Element ${}F\in I$, ${}F\neq 0$, herrührt, sagen wir ${}m=\operatorname {grad} \,(F)$. Wir behaupten, dass ${}I=(F)$ ist. Die Inklusion ${}\supseteq$ ist klar. Zum Beweis von ${}\subseteq$ sei ${}P\in I$ gegeben. Aufgrund von Satz 16.9 gilt

$P=FQ+R{\text{ mit }}\operatorname {grad} \,(R)<\operatorname {grad} \,(F){\text{ oder }}R=0.$

Wegen ${}R\in I$ und der Minimalität von ${}\operatorname {grad} \,(F)$ kann der erste Fall nicht eintreten. Also ist ${}R=0$ und ${}P$ ist ein Vielfaches von ${}F$.

$\Box$

Definition

Es sei ${}K$ ein Körper und seien ${}a_{0},a_{1},\ldots ,a_{n}\in K$. Eine Funktion

$P\colon K\longrightarrow K,\,x\longmapsto P(x),$

mit

${}P(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+\cdots +a_{n}x^{n}\,$

heißt Polynomfunktion.

Man muss streng zwischen Polynomen und Polynomfunktionen unterscheiden, insbesondere für ${}K=\mathbb {Z} /(p)$. Das Polynom

$X^{p}-X$

hat beispielsweise nach dem

kleinen Fermat (Satz 14.14) für jedes ${}a\in K$ den Wert ${}a^{p}-a=0$. D.h. die durch dieses Polynom definierte Polynomfunktion ist die Nullfunktion, obwohl das Polynom selbst nicht das Nullpolynom ist.

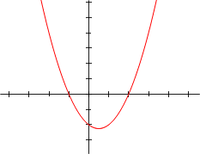
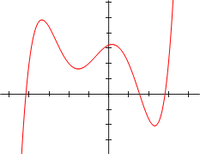
Bei ${}K=\mathbb {R}$ lassen sich die Polynomfunktionen graphisch veranschaulichen.

<< | Kurs:Einführung in die Algebra (Osnabrück 2009) | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)