Kurs:Elemente der Algebra (Osnabrück 2024-2025)/Vorlesung 4

Komplexe Exponentialfunktion

Wir erläutern kurz und ohne Beweise einen weiteren Zugang zur Multiplikation von komplexen Zahlen. Zunächst kann man innerhalb der komplexen Zahlen wie bei den reellen Zahlen von konvergenten Folgen sprechen, die Definition überträgt sich unmittelbar, wobei der komplexe Betrag den reellen Betrag ersetzt. In Satz 53.8 (Grundkurs Mathematik (Osnabrück 2022-2023)) haben wir erwähnt, dass die reelle Exponentialfunktion ${}e^{x}$ durch

${}e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\,$

beschrieben werden kann, wobei die unendliche Summe für jedes ${}x$ konvergiert. Diese Konvergenz kann man auch für komplexe Zahlen nachweisen und gelangt so zur komplexen Exponentialfunktion.

Definition

Die Abbildung

${\mathbb {C} }\longrightarrow {\mathbb {C} },\,z\longmapsto \exp z:=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}},$

heißt (komplexe) Exponentialfunktion.

Auch die Funktionalgleichung gilt nach wie vor.

Satz

Für komplexe Zahlen ${}z,w\in {\mathbb {C} }$ gilt

${}\exp \left(z+w\right)=\exp z\cdot \exp w\,.$

Überraschend ist hingegen, dass sich im Komplexen eine Beziehung zwischen der komplexen Exponentialfunktion und den trigonometrischen Funktionen Sinus und Kosinus ergibt.

Satz

Für ${}z=x+{\mathrm {i} }y$ ist

${}\exp z=(\exp x)\exp {\mathrm {i} }y=(\exp x)(\cos y+{\mathrm {i} }\sin y)\,.$

Speziell gilt die eulersche Formel

${}\exp {\mathrm {i} }y=\cos y+{\mathrm {i} }\sin y\,.$

Spezialfälle davon sind

${}\exp 2\pi {\mathrm {i} }=1\,$

und

${}\exp \pi {\mathrm {i} }=-1\,,$

was man auch gern als

${}1+\exp \pi {\mathrm {i} }=0\,$

schreibt.

Satz

Zu jeder komplexen Zahl ${}z\in {\mathbb {C} }$, ${}z\neq 0$,

gibt es eine eindeutige Darstellung

${}z=r\cdot \exp({\mathrm {i} }\varphi )=re^{{\mathrm {i} }\varphi }=r(\cos \varphi +{\mathrm {i} }\sin \varphi )\,$

mit ${}r\in \mathbb {R} _{+}$ und mit ${}\varphi \in [0,2\pi [$.

Dies ist anschaulich klar. ${}\varphi$ ist der Winkel der durch ${}z$ und dem Nullpunkt definierten Halbgerade, und ${}e^{{\mathrm {i} }\varphi }$ ist der zugehörige Punkt auf dem Einheitskreis.

Korollar

Für zwei komplexe Zahlen ${}z_{1}=r_{1}e^{{\mathrm {i} }\varphi _{1}}$ und ${}z_{2}=r_{2}e^{{\mathrm {i} }\varphi _{2}}$ ist

${}z_{1}z_{2}=r_{1}r_{2}e^{{\mathrm {i} }(\varphi _{1}+\varphi _{2})}\,.$

Zwei komplexe Zahlen ${}\neq 0$ werden also miteinander multipliziert, indem man ihre Beträge in ${}\mathbb {R} _{+}$ multipliziert und ihre Argumente (Winkel) addiert.

Polynomringe in einer Variablen

Zu einem kommutativen Ausgangsring wie ${}\mathbb {Z}$ oder ${}\mathbb {R}$ und einer fixierten Variablen ${}X$ kann man sich fragen, welche Terme man mit dieser Variablen über diesem Ring „basteln“ kann. Dazu gehören

$5,\,3X+3,\,3(X+1),\,(2X-6)(4X+3),\,X\cdot (X\cdot X),\,5+3X-6X^{2}+7X^{3},\,X^{2}-4+5X^{2}+7X-13X,$

wobei wir Potenzschreibweise verwendet und einige Klammern weggelassen haben. Als Terme sind ${}3X+3$ und ${}3(X+1)$ verschieden. Bei jeder Interpretation von ${}X$ in einem Ring sind diese Ausdrücke aber gleich. Der Polynomring besteht aus genau diesen Termen, wobei allerdings Terme miteinander identifiziert werden, wenn dies in jedem kommutativen Ring gilt (die Menge aller Terme ist kein Ring)!

Definition

Der Polynomring über einem kommutativen Ring ${}R$ besteht aus allen Polynomen

$P=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{n}X^{n}$

mit ${}a_{i}\in R,\,i=0,\ldots ,n,\,n\in \mathbb {N}$,

und mit komponentenweiser Addition und einer Multiplikation, die durch distributive Fortsetzung der Regel

${}X^{n}\cdot X^{m}:=X^{n+m}\,$

definiert ist.

Ein Polynom

${}P=\sum _{i=0}^{n}a_{i}X^{i}=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{n}X^{n}\,$

ist formal gesehen nichts anderes als das Tupel ${}(a_{0},a_{1},\ldots ,a_{n})$, die die Koeffizienten des Polynoms heißen. Der Ring ${}R$ heißt in diesem Zusammenhang der Grundring des Polynomrings. Aufgrund der komponentenweisen Definition der Addition liegt unmittelbar eine Gruppe vor, mit dem Nullpolynom (bei dem alle Koeffizienten null sind) als neutralem Element. Zwei Polynome sind genau dann gleich, wenn sie in allen ihren Koeffizienten übereinstimmen. Die Polynome mit ${}a_{i}=0$ für alle ${}i\geq 1$ heißen konstante Polynome, man schreibt sie einfach als ${}a_{0}$. Ein von ${}0$ verschiedenes Polynom kann man als ${}\sum _{i=0}^{n}a_{i}X^{i}$ mit ${}a_{n}\neq 0$ schreiben. Der Koeffizient ${}a_{n}$ heißt dann der Leitkoeffizient des Polynoms.

Die für ein einfaches Tupel zunächst ungewöhnliche Schreibweise deutet in suggestiver Weise an, wie die Multiplikation aussehen soll, das Produkt ${}X^{i}X^{j}$ ist nämlich durch die Addition der Exponenten gegeben. Dabei nennt man ${}X$ die Variable des Polynomrings. Für beliebige Polynome ergibt sich die Multiplikation aus dieser einfachen Multiplikationsbedingung durch distributive Fortsetzung gemäß der Vorschrift, „alles mit allem“ zu multiplizieren. Die Multiplikation ist also explizit durch folgende Regel gegeben:

${\left(\sum _{i=0}^{n}a_{i}X^{i}\right)}\cdot {\left(\sum _{j=0}^{m}b_{j}X^{j}\right)}=\sum _{k=0}^{n+m}c_{k}X^{k}{\text{ mit }}c_{k}=\sum _{r=0}^{k}a_{r}b_{k-r}.$

Beispielsweise ist

${}{\begin{aligned}{\left({\mathrm {i} }X^{2}+(3-{\mathrm {i} })X+5\right)}{\left(-X^{2}+4X+2{\mathrm {i} }\right)}&=-{\mathrm {i} }X^{4}+(4{\mathrm {i} }-(3-{\mathrm {i} }))X^{3}+(2{\mathrm {i} }{\mathrm {i} }+(3-{\mathrm {i} })4-5)X^{2}+((3-{\mathrm {i} })2{\mathrm {i} }+20)X+10{\mathrm {i} }\\&=-{\mathrm {i} }X^{4}+(-3+5{\mathrm {i} })X^{3}+(5-4{\mathrm {i} })X^{2}+(22+6{\mathrm {i} })X+10{\mathrm {i} }.\,\end{aligned}}$

Lemma

Es sei ${}R$ ein kommutativer Ring und sei ${}R[X]$ der Polynomring über ${}R$. Dann gelten folgende Aussagen.

1. ${}R$ ist ein Unterring von ${}R[X]$.
2. ${}R$ ist genau dann ein Integritätsbereich, wenn ${}R[X]$ ein Integritätsbereich ist.

Beweis

1. Ein Element ${}r\in R$ wird als konstantes Polynom aufgefasst, wobei es egal ist, ob man Addition und Multiplikation in ${}R$ oder in ${}R[X]$ ausführt.
2. Wenn ${}R[X]$ integer ist, so überträgt sich dies sofort auf den Unterring ${}R$. Es sei also ${}R$ ein Integritätsbereich und seien ${}P=\sum _{i=0}^{n}a_{i}X^{i}$ und ${}Q=\sum _{j=0}^{m}b_{j}X^{j}$ zwei von null verschiedene Polynome. Wir können annehmen, dass ${}a_{n}$ und ${}b_{m}$ von null verschieden sind. Dann ist ${}a_{n}b_{m}\neq 0$ und dies ist der Leitkoeffizient des Produktes ${}PQ$, das damit nicht null sein kann.

$\Box$

Korollar

Es sei ${}R$ ein kommutativer Ring und sei ${}S\subseteq R$ ein Unterring.

Dann ist auch ${}S[X]$ ein Unterring von ${}R[X]$.

Beweis

Siehe Aufgabe 4.6.

$\Box$

Die vorstehende Aussage bedeutet einfach, dass man ein Polynom mit Koeffizienten aus ${}S$ direkt auch als Polynom mit Koeffizienten aus ${}R$ auffassen kann. So ist ein Polynom mit ganzzahligen Koeffizienten insbesondere auch ein Polynom mit rationalen Koeffizienten und mit reellen Koeffizienten. Die Addition und die Multiplikation von zwei Polynomen hängt nicht davon ab, ob man sie über einem kleineren oder einem größeren Grundring ausrechnet, so lange dieser nur alle beteiligten Koeffizienten enthält. Es gibt aber auch viele wichtige Eigenschaften, die vom Grundring abhängen, wie beispielsweise die Eigenschaft, irreduzibel zu sein, siehe Beispiel 6.8.

In ein Polynom ${}P\in R[X]$ kann man ein Element ${}r\in R$ einsetzen. Dabei ersetzt man überall die Variable ${}X$ durch ${}r$ und rechnet das Ergebnis in ${}R$ aus. Dieses Ergebnis wird mit ${}P(r)$ bezeichnet. Ein fixiertes Element ${}r\in R$ definiert dann eine Abbildung (die Auswertungsabbildung zu ${}r$)

$R[X]\longrightarrow R,\,P\longmapsto P(r).$

Andererseits definiert ein fixiertes Polynom ${}P\in R[X]$ die zugehörige Polynomfunktion, die durch

$R\longrightarrow R,\,x\longmapsto P(x).$

Diese wird insbesondere bei einem Körper ${}R=K$ studiert, siehe weiter unten.

Der Grad eines Polynoms

Definition

Der Grad eines von ${}0$ verschiedenen Polynoms

${}P=a_{0}+a_{1}X+a_{2}X^{2}+\cdots +a_{n}X^{n}\,$

mit ${}a_{n}\neq 0$ ist ${}n$.

Wenn der Leitkoeffizient ${}a_{n}=1$ ist, so nennt man das Polynom normiert. Dem Nullpolynom wird im Allgemeinen kein Grad zugewiesen; manchmal sind gewisse Gleichungen oder Bedingungen aber auch so zu verstehen, dass dem Nullpolynom jeder Grad zugewiesen wird. Polynome vom Grad ${}0$ heißen konstante Polynome, Polynome vom Grad ${}1$ heißen affin-lineare Polynome und Polynome vom Grad ${}2$ heißen quadratische Polynome.

Lemma

Es sei ${}R$ ein kommutativer Ring und sei ${}R[X]$ der Polynomring über ${}R$. Dann gelten für den Grad folgende Aussagen.

1. ${}\operatorname {grad} \,(P+Q)\leq \max\{\operatorname {grad} \,(P),\,\operatorname {grad} \,(Q)\}\,.$

2. ${}\operatorname {grad} \,(P\cdot Q)\leq \operatorname {grad} \,(P)+\operatorname {grad} \,(Q)\,.$

3. Wenn ${}R$ ein Integritätsbereich ist, so gilt in (2) die Gleichheit.

Beweis

Siehe Aufgabe 4.7.

$\Box$

Polynomringe in mehreren Variablen

Die Konstruktion von Polynomringen aus einem Grundring kann man iterieren. Aus ${}R$ kann man ${}R[X]$ machen und daraus mit einer neuen Variablen den Ring ${}(R[X])[Y]$ bilden. Für diesen Ring schreibt man auch ${}R[X,Y]$. Ein Element darin hat die Gestalt

$\sum _{i,j}a_{ij}X^{i}Y^{j},$

wobei die Summe endlich ist. Ein Ausdruck der Form ${}X^{i}Y^{j}$ heißt Monom. Polynome kann man auf unterschiedliche Art sortieren. Man kann die Potenz einer Variablen (etwa ${}Y$) herausnehmen und schauen, welche Polynome in ${}X$ sich darauf beziehen. Dann sieht ein Polynom folgendermaßen aus:

$2+3X-X^{2}-5X^{3}+(1+3X-X^{2}+3X^{5})Y+(4+X+7X^{2}-6X^{4})Y^{2}+(2-X^{3})Y^{3}.$

Oder man kann entlang dem Summengrad sortieren, dies ergibt

$2+3X+Y-X^{2}+3XY+4Y^{2}-5X^{3}-X^{2}Y+XY^{2}+2Y^{3}+7X^{2}Y^{2}+3X^{5}Y+6X^{4}Y^{2}-X^{3}Y^{3}.$

Polynomiale Identitäten haben viel mit allgemeingültigen Termidentitäten zu tun. In ${}\mathbb {Z} [X,Y]$ gilt beispielsweise

$(X+Y)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}X^{k}Y^{n-k}.$

Diese Identität zwischen zwei Polynomen entspricht der allgemeinen binomischen Formel. Einerseits ist sie ein Spezialfall davon, da wir in dem kommutativen Ring ${}\mathbb {Z} [X,Y]$ sind und die speziellen Elemente ${}X$ und ${}Y$ anschauen. Andererseits kann man aus dieser polynomialen Identität die allgemeine binomische Formel zurückgewinnen, da man für ${}X$ und ${}Y$ beliebige Elemente ${}a$ und ${}b$ eines kommutativen Ringes einsetzen kann (und man weiß, wie man ganze Zahlen in jedem Ring interpretiert) und sich dabei die Identität erhält. Natürlich gibt es auch Polynomringe in beliebig vielen Variablen, dafür schreibt man ${}R[X_{1},X_{2},\ldots ,X_{n}]$.

Polynomringe über einem Körper

Für uns sind zunächst die Polynomringe über einem Körper von besonderer Bedeutung.

Definition

Es sei ${}K$ ein Körper und seien ${}a_{0},a_{1},\ldots ,a_{n}\in K$. Eine Funktion

$P\colon K\longrightarrow K,\,x\longmapsto P(x),$

mit

${}P(x)=\sum _{i=0}^{n}a_{i}x^{i}=a_{0}+a_{1}x+\cdots +a_{n}x^{n}\,$

heißt Polynomfunktion.

Man muss zwischen Polynomen und Polynomfunktionen unterscheiden, insbesondere für ${}K=\mathbb {Z} /(p)$.

Das Polynom

$X^{p}-X$

hat beispielsweise nach

dem kleinen Fermat für jedes ${}a\in K$ den Wert ${}a^{p}-a=0$. D.h. die durch dieses Polynom definierte Polynomfunktion ist die Nullfunktion, obwohl das Polynom selbst nicht das Nullpolynom ist.

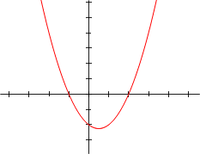
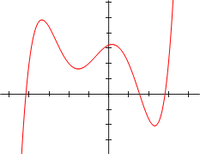
Bei ${}K=\mathbb {R}$ lassen sich die Polynomfunktionen graphisch veranschaulichen.

Eine wichtige Frage ist, für welche Elemente ${}x\in K$ die Polynomfunktion einen bestimmten Wert annimmt. Hierbei ist insbesondere der Wert ${}0$ wichtig, da ja die Gleichung ${}P(x)=a$ äquivalent zu

${}P(x)-a=0\,$

ist und ${}P-a$ wieder ein Polynom ist. Für affin-lineare Polynome ${}aX+b$ (mit ${}a\neq 0$) ist ${}x={\frac {-b}{a}}$ die einzige Lösung. Für quadratische Polynome der reinen Form ${}X^{2}+c$ sind die Quadratwurzeln von ${}-c$ aus ${}K$, falls sie denn existieren, die Lösungen. Für ein quadratisches Polynom ${}aX^{2}+bX+c$ kann man das Bestimmen der Nullstellen durch quadratisches Ergänzen auf die reine Form zurückführen, siehe Aufgabe 4.12.

Der folgende Satz heißt Interpolationssatz und beschreibt die Interpolation von vorgegebenen Funktionswerten durch Polynome.

Satz

Es sei ${}K$ ein Körper und es seien ${}n$ verschiedene Elemente ${}a_{1},\ldots ,a_{n}\in K$ und ${}n$ Elemente ${}b_{1},\ldots ,b_{n}\in K$ gegeben.

Dann gibt es ein eindeutiges Polynom ${}P\in K[X]$ vom Grad ${}\leq n-1$ derart, dass ${}P{\left(a_{i}\right)}=b_{i}$ für alle ${}i$ ist.

Beweis

Wir beweisen die Existenz und betrachten zuerst die Situation, wo ${}b_{j}=0$ ist für alle ${}j\neq i$ für ein festes ${}i$. Dann ist

$(X-a_{1})\cdots (X-a_{i-1})(X-a_{i+1})\cdots (X-a_{n})$

ein Polynom vom Grad ${}n-1$, das an den Stellen ${}a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}$ den Wert ${}0$ hat. Das Polynom

${\frac {b_{i}}{(a_{i}-a_{1})\cdots (a_{i}-a_{i-1})(a_{i}-a_{i+1})\cdots (a_{i}-a_{n})}}(X-a_{1})\cdots (X-a_{i-1})(X-a_{i+1})\cdots (X-a_{n})$

hat an diesen Stellen ebenfalls eine Nullstelle, zusätzlich aber noch bei ${}a_{i}$ den Wert ${}b_{i}$. Nennen wir dieses Polynom ${}P_{i}$. Dann ist

${}P=P_{1}+P_{2}+\cdots +P_{n}\,$

das gesuchte Polynom. An der Stelle ${}a_{i}$ gilt ja

${}P_{j}(a_{i})=0\,$

für ${}j\neq i$ und ${}P_{i}(a_{i})=b_{i}$.

Die Eindeutigkeit folgt aus Korollar 5.6.

$\Box$

<< | Kurs:Elemente der Algebra (Osnabrück 2024-2025) | >> PDF-Version dieser Vorlesung Arbeitsblatt zur Vorlesung (PDF)