Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Teil I/Vorlesung 5/kontrolle

„Wenn ich weiter geblickt habe, so deshalb, weil ich auf den Schultern von Riesen stehe“

Isaac Newton

Anordnungseigenschaften der reellen Zahlen

Bekanntlich kann man die reellen Zahlen mit einer Geraden identifizieren. Auf der Zahlengeraden liegen von zwei Punkten einer weiter rechts als der andere, was bedeutet, dass sein Wert größer ist. Wir besprechen nun diese Anordnungseigenschaften der reellen Zahlen.

Definition Referenznummer erstellen

Ein Körper ${}K$ heißt angeordneter Körper, wenn es zwischen den Elementen von ${}K$ eine Beziehung ${}>$ („größer als“) gibt, die die folgenden Eigenschaften erfüllt (${}a\geq b$ bedeutet ${}a>b$ oder ${}a=b$).

1. Für je zwei Elemente ${}a,b\in K$ gilt entweder ${}a>b$ oder ${}a=b$ oder ${}b>a$.
2. Aus ${}a\geq b$ und ${}b\geq c$ folgt ${}a\geq c$ (für beliebige ${}a,b,c\in K$).
3. Aus ${}a\geq b$ folgt ${}a+c\geq b+c$ (für beliebige ${}a,b,c\in K$).
4. Aus ${}a\geq 0$ und ${}b\geq 0$ folgt ${}ab\geq 0$ (für beliebige ${}a,b\in K$).

Die rationalen Zahlen ${}\mathbb {Q}$ als auch die reellen Zahlen ${}\mathbb {R}$ bilden mit den natürlichen Vergleichsordnungen einen angeordneten Körper. Im Zahlenstrahl bedeutet

${}a\geq b\,,$

dass ${}a$ mindestens so weit rechts wie ${}b$ liegt. Die ersten beiden Eigenschaften drücken aus, dass auf ${}K$ eine totale (oder lineare) Ordnung vorliegt; die in (2) beschriebene Eigenschaft heißt Transitivität.

Statt ${}a>b$ schreibt man auch ${}b<a$ („kleiner als“) und statt ${}a\geq b$ schreibt man auch ${}b\leq a$. Ein Element ${}a\in K$ in einem angeordneten Körper nennt man positiv, wenn ${}a>0$ ist, und negativ, wenn ${}a<0$ ist. Die ${}0$ ist demnach weder positiv noch negativ, und jedes Element ist entweder positiv oder negativ oder gleich ${}0$. Die Elemente ${}a$ mit ${}a\geq 0$ nennt man dann einfach nichtnegativ und die Elemente ${}a$ mit ${}a\leq 0$ nichtpositiv.

Lemma Lemma 5.2 ändern

In einem angeordneten Körper gelten die folgenden Eigenschaften.

1. ${}1\geq 0$.
2. Es ist ${}a\geq 0$ genau dann, wenn ${}-a\leq 0$ ist.
3. Es ist ${}a\geq b$ genau dann, wenn ${}a-b\geq 0$ ist.
4. Es ist ${}a\geq b$ genau dann, wenn ${}-a\leq -b$ ist.
5. Aus ${}a\geq b$ und ${}c\geq d$ folgt ${}a+c\geq b+d$.
6. Aus ${}a\geq b$ und ${}c\geq 0$ folgt ${}ac\geq bc$.
7. Aus ${}a\geq b$ und ${}c\leq 0$ folgt ${}ac\leq bc$.
8. Aus ${}a\geq b\geq 0$ und ${}c\geq d\geq 0$ folgt ${}ac\geq bd$.
9. Aus ${}a\geq 0$ und ${}b\leq 0$ folgt ${}ab\leq 0$.
10. Aus ${}a\leq 0$ und ${}b\leq 0$ folgt ${}ab\geq 0$.

Beweis

Siehe Aufgabe 5.5.

$\Box$

Lemma Referenznummer erstellen

In einem angeordneten Körper gelten die folgenden Eigenschaften.

1. Aus ${}x>0$ folgt auch ${}x^{-1}>0$.
2. Aus ${}x<0$ folgt auch ${}x^{-1}<0$.
3. Für ${}x>0$ ist ${}x\geq 1$ genau dann, wenn ${}x^{-1}\leq 1$ ist.
4. Aus ${}x\geq y>0$ folgt ${}x^{-1}\leq y^{-1}$.
5. Für positive Elemente ${}x,y$ ist ${}x\geq y$ äquivalent zu ${}{\frac {x}{y}}\geq 1$.

Beweis

Siehe Aufgabe 5.7, Aufgabe 5.32, Aufgabe 5.8, Aufgabe 5.9 und Aufgabe 5.10.

$\Box$

Wir besprechen nun eine weitere Anordungseigenschaft der reellen Zahlen, das sogenannte Archimedes-Axiom. Um dieses formulieren zu können, müssen wir uns zunächst klar machen, dass in jedem Körper ${}K$ jede natürliche Zahl ${}n$ eine sinnvolle und eindeutige Interpretation hat. Dies ist nicht selbstverständlich, da ja in der Axiomatik eines Körpers zwar eine ${}0$ und eine ${}1$ vorkommt, aber keine ${}2,3,...$. Wir legen daher einfach über die Addition im Körper die Bedeutung dieser Zahlen fest, also

${}2=1+1\,,$

${}3=2+1=1+1+1$, u.s.w. Dabei kann passieren, dass eine positive natürliche Zahl in einem Körper gleich ${}0$ ist, im Körper mit zwei Elementen ist beispielsweise ${}0=2=4=6=\ldots$ und ${}1=3=5=7=\ldots$. Eine negative ganze Zahlen ${}-n$ kann man in jedem Körper als das Negative (im Körper) von ${}n$ interpretieren. Bei einem angeordneten Körper ${}K$ ist aber die natürliche Abbildung ${}\mathbb {Z} \rightarrow K$ injektiv. Damit können wir das noch ausstehende Axiom formulieren.

Archimedes (ca. 287 -212 v. C.)

Definition Referenznummer erstellen

Es sei ${}K$ ein angeordneter Körper. Dann heißt ${}K$ archimedisch angeordnet, wenn das folgende Archimedische Axiom gilt, d.h. wenn es zu jedem ${}x\in K$ eine natürliche Zahl ${}n$ mit

${}n\geq x\,$

gibt.

Die reellen Zahlen (ebenso die rationalen Zahlen) erfüllen das Archimedische Axiom, sie bilden also einen archimedisch angeordneten Körper. Die folgenden Folgerungen aus dem Archimedes-Axiom gelten also für die reellen Zahlen. Wir werden sie direkt nur für die reellen Zahlen selbst formulieren, da man sogar jeden archimedisch angeordneten Körper als Unterkörper der reellen Zahlen erhalten kann. In Aufgabe 6.22 wird ein angeordneter Körper beschrieben, der nicht archimedisch angeordnet ist. Aufgrund von Aufgabe ***** {{:Kurs:Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Angeordneter Körper/Enthält Q/Verknüpfung und Ordnung/Aufgabe/Aufgabereferenznummer/Angeordneter Körper/Enthält Q/Verknüpfung und Ordnung/Aufgabe/Aufgabereferenznummer}} enthält ein angeordneter Körper nicht nur die ganzen Zahlen, sondern auch die rationalen Zahlen.

Lemma

1. Zu ${}x,y\in \mathbb {R}$ mit ${}x>0$ gibt es ein ${}n\in \mathbb {N}$ mit ${}nx\geq y$.
2. Zu ${}x>0$ gibt es eine natürliche Zahl ${}n$ mit ${}{\frac {1}{n}}<x$.
3. Zu zwei reellen Zahlen ${}x<y$ gibt es auch eine rationale Zahl ${}n/k$ (mit ${}n\in \mathbb {Z}$, ${}k\in \mathbb {N} _{+}$) mit

   ${}x<{\frac {n}{k}}<y\,.$

Beweis

(1). Wir betrachten ${}y/x$. Aufgrund des Archimedes-Axioms gibt es ein ${}n$ mit ${}n\geq y/x$. Da ${}x$ positiv ist, gilt nach Lemma 5.2  (6) auch ${}nx\geq y$. Für (2) und (3) siehe Aufgabe 5.18.

$\Box$

Definition Referenznummer erstellen

Für reelle Zahlen ${}a,b$, ${}a\leq b$, nennt man

• ${}[a,b]={\left\{x\in \mathbb {R} \mid x\geq a{\text{ und }}x\leq b\right\}}$

das abgeschlossene Intervall.

• ${}]a,b[={\left\{x\in \mathbb {R} \mid x>a{\text{ und }}x<b\right\}}$

das offene Intervall.

• ${}]a,b]={\left\{x\in \mathbb {R} \mid x>a{\text{ und }}x\leq b\right\}}$

das linksseitig offene Intervall.

• ${}[a,b[={\left\{x\in \mathbb {R} \mid x\geq a{\text{ und }}x<b\right\}}$

das rechtsseitig offene Intervall.

Für das offene Intervall wird häufig auch ${}(a,b)$ geschrieben. Die Zahlen ${}a$ und ${}b$ heißen die Grenzen des Intervalls (oder Randpunkte des Intervalls), genauer spricht man von unterer und oberer Grenze. Die Bezeichnung linksseitig und rechtsseitig bei den beiden letzten Intervallen (die man auch als halboffen bezeichnet) rühren von der üblichen Repräsentierung der reellen Zahlen als Zahlengerade her, bei der rechts die positiven Zahlen stehen. Manchmal werden auch Schreibweisen wie ${}[a,\infty ]$ verwendet. Dies bedeutet nicht, dass es in ${}\mathbb {R}$ ein Element ${}\infty$ gibt, sondern ist lediglich eine kurze Schreibweise für ${}{\left\{x\in \mathbb {R} \mid x\geq a\right\}}$. Ferner verwendet man Schreibweisen wie

$\mathbb {R} _{+},\,\mathbb {R} _{-},\,\mathbb {R} _{\geq 0}=\mathbb {R} _{+}^{0},\,\mathbb {R} _{\leq 0}=\mathbb {R} _{-}^{0}$

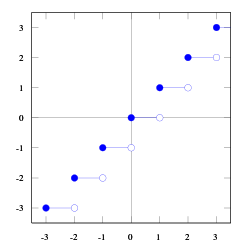
oder Ähnliches. Für die reellen Zahlen bilden die ganzzahligen Intervalle ${}[n,n+1[$, ${}n\in \mathbb {Z}$, eine disjunkte Überdeckung. Deshalb ist die folgende Definition sinnvoll.

Definition Referenznummer erstellen

Zu einer reellen Zahl ${}x$ ist die Gaußklammer ${}\left\lfloor x\right\rfloor$ durch

$\left\lfloor x\right\rfloor =n,{\text{ falls }}x\in [n,n+1[{\text{ und }}n\in \mathbb {Z} ,$

definiert.

Die Anordnungseigenschaften erlauben es auch, von wachsenden und fallenden Funktionen zu sprechen.

Definition Referenznummer erstellen

Es sei ${}I\subseteq \mathbb {R}$ ein Intervall und

$f\colon I\longrightarrow \mathbb {R}$

eine Funktion. Dann heißt ${}f$ wachsend, wenn

$f(x')\geq f(x){\text{ für alle }}x,x'\in I{\text{ mit }}x'\geq x{\text{ gilt}},$

streng wachsend, wenn

$f(x')>f(x){\text{ für alle }}x,x'\in I{\text{ mit }}x'>x{\text{ gilt}},$

fallend, wenn

$f(x')\leq f(x){\text{ für alle }}x,x'\in I{\text{ mit }}x'\geq x{\text{ gilt}},$

streng fallend, wenn

$f(x')<f(x){\text{ für alle }}x,x'\in I{\text{ mit }}x'>x{\text{ gilt}}.$

Der Betrag

Definition Referenznummer erstellen

Für eine reelle Zahl ${}x\in \mathbb {R}$ ist der Betrag folgendermaßen definiert.

${}\vert {x}\vert ={\begin{cases}x\,,{\text{ falls }}x\geq 0\,,\\-x,\,{\text{ falls }}x<0\,.\end{cases}}\,$

Der Betrag ist also nie negativ und hat nur bei ${}x=0$ den Wert ${}0$, sonst ist er immer positiv. Die Gesamtabbildung

$\mathbb {R} \longrightarrow \mathbb {R} ,\,x\longmapsto \vert {x}\vert ,$

nennt man auch Betragsfunktion. Der Funktionsgraph setzt sich aus zwei Halbgeraden zusammen; eine solche Funktion nennt man auch stückweise linear.

Lemma Referenznummer erstellen

Die reelle Betragsfunktion

$\mathbb {R} \longrightarrow \mathbb {R} ,\,x\longmapsto \vert {x}\vert ,$

erfüllt folgende Eigenschaften (dabei seien ${}x,y$ beliebige reelle Zahlen).

1. Es ist ${}\vert {x}\vert \geq 0$.
2. Es ist ${}\vert {x}\vert =0$ genau dann, wenn ${}x=0$ ist.
3. Es ist ${}\vert {x}\vert =\vert {y}\vert$ genau dann, wenn ${}x=y$ oder ${}x=-y$ ist.
4. Es ist ${}\vert {y-x}\vert =\vert {x-y}\vert$.
5. Es ist ${}\vert {xy}\vert =\vert {x}\vert \vert {y}\vert$.
6. Für ${}x\neq 0$ ist ${}\vert {x^{-1}}\vert =\vert {x}\vert ^{-1}$.
7. Es ist ${}\vert {x+y}\vert \leq \vert {x}\vert +\vert {y}\vert$ (Dreiecksungleichung für den Betrag).
8. Es ist ${}\vert {x+y}\vert \geq \vert {x}\vert -\vert {y}\vert$.

Beweis

Siehe Aufgabe 5.20.

$\Box$

Bernoullische Ungleichung

Die Bernoullische Ungleichung für $n=3$.

Die folgende Aussage heißt Bernoulli-Ungleichung.

Satz Referenznummer erstellen

Für jede reelle Zahl ${}x\geq -1$ und eine natürliche Zahl ${}n$

gilt die Abschätzung

${}(1+x)^{n}\geq 1+nx\,.$

Beweis

Wir führen Induktion über ${}n$. Bei ${}n=0$ steht beidseitig ${}1$, sodass die Aussage gilt. Es sei nun die Aussage für ${}n$ bereits bewiesen. Dann ist

${}{\begin{aligned}(1+x)^{n+1}&=(1+x)^{n}(1+x)\\&\geq (1+nx)(1+x)\\&=1+(n+1)x+nx^{2}\\&\geq 1+(n+1)x,\end{aligned}}$

da Quadrate (und positive Vielfache davon) in einem angeordneten Körper nichtnegativ sind.

$\Box$

Die komplexen Zahlen

Wir führen nun ausgehend von den reellen Zahlen die komplexen Zahlen ein. Zwar haben wir noch nicht alle Eigenschaften der reellen Zahlen kennengelernt, insbesondere haben wir noch nicht die Vollständigkeit diskutiert, die ${}\mathbb {R}$ von ${}\mathbb {Q}$ unterscheidet, doch ist dies für die Konstruktion von ${}{\mathbb {C} }$ unerheblich. Verwenden werden weiter unten, dass jede nichtnegative reelle Zahl eine eindeutige Quadratwurzel besitzt. Damit haben wir alle für die Anfängervorlesungen relevanten Zahlenbereiche zur Verfügung.

Definition Referenznummer erstellen

Die Menge ${}\mathbb {R} ^{2}$ mit ${}0:=(0,0)$ und ${}1:=(1,0)$, mit der komponentenweisen Addition und der durch

${}(a,b)\cdot (c,d):=(ac-bd,ad+bc)\,$

definierten Multiplikation nennt man Körper der komplexen Zahlen. Er wird mit

${\mathbb {C} }$

bezeichnet.

Die Addition ist also einfach die vektorielle Addition im ${}\mathbb {R} ^{2}$, während die Multiplikation eine neuartige Verknüpfung ist, die zwar numerisch einfach durchführbar ist, an die man sich aber dennoch gewöhnen muss. Wir werden in Fakt ***** noch eine geometrische Interpretation für die komplexe Multiplikation kennenlernen.

Lemma Referenznummer erstellen

Die komplexen Zahlen

bilden einen Körper.

Beweis

Siehe Aufgabe 5.27.

$\Box$

Wir lösen uns von der Paarschreibweise und schreiben

${}a+b{\mathrm {i} }:=(a,b)\,.$

Insbesondere ist ${}{\mathrm {i} }=(0,1)$, diese Zahl heißt imaginäre Einheit. Diese Zahl hat die wichtige Eigenschaft

${}{\mathrm {i} }^{2}=-1\,.$

Aus dieser Eigenschaft ergeben sich sämtliche algebraischen Eigenschaften der komplexen Zahlen durch die Körpergesetze. So kann man sich auch die obige Multiplikationsregel merken, es ist ja

${}(a+b{\mathrm {i} })(c+d{\mathrm {i} })=ac+ad{\mathrm {i} }+b{\mathrm {i} }c+b{\mathrm {i} }d{\mathrm {i} }=ac+bd{\mathrm {i} }^{2}+(ad+bc){\mathrm {i} }=ac-bd+(ad+bc){\mathrm {i} }\,.$

Wir fassen eine reelle Zahl ${}a$ als die komplexe Zahl ${}a+0{\mathrm {i} }=(a,0)$ auf. In diesem Sinne ist ${}\mathbb {R} \subset {\mathbb {C} }$. Es ist gleichgültig, ob man zwei reelle Zahlen als reelle Zahlen oder als komplexe Zahlen addiert oder multipliziert.

Definition Referenznummer erstellen

Zu einer komplexen Zahl

${}z=a+b{\mathrm {i} }\,$

heißt

${}\operatorname {Re} \,{\left(z\right)}=a\,$

der Realteil von ${}z$ und

${}\operatorname {Im} \,{\left(z\right)}=b\,$

heißt der Imaginärteil von ${}z$.

Man sollte sich allerdings die Menge der komplexen Zahlen nicht als etwas vorstellen, was weniger real als andere Zahlensysteme ist. Die Konstruktion der komplexen Zahlen aus den reellen Zahlen ist bei Weitem einfacher als die Konstruktion der reellen Zahlen aus den rationalen Zahlen. Allerdings war es historisch ein langer Prozess, bis die komplexen Zahlen als Zahlen anerkannt wurden; das Irreale daran ist, dass sie einen Körper bilden, der nicht angeordnet werden kann, und dass es sich daher scheinbar um keine Größen handelt, mit denen man sinnvollerweise etwas messen kann.

Man kann sich die komplexen Zahlen als die Punkte in einer Ebene vorstellen; für die additive Struktur gilt ja einfach ${}{\mathbb {C} }=\mathbb {R} ^{2}$. In diesem Zusammenhang spricht man von der Gaussschen Zahlenebene. Die horizontale Achse nennt man dann die reelle Achse und die vertikale Achse die imaginäre Achse.

Lemma Referenznummer erstellen

Real- und Imaginärteil von komplexen Zahlen erfüllen folgende Eigenschaften (für ${}z$ und ${}w$ aus ${}{\mathbb {C} }$).

1. Es ist ${}z=\operatorname {Re} \,{\left(z\right)}+\operatorname {Im} \,{\left(z\right)}{\mathrm {i} }$.
2. Es ist ${}\operatorname {Re} \,{\left(z+w\right)}=\operatorname {Re} \,{\left(z\right)}+\operatorname {Re} \,{\left(w\right)}$.
3. Es ist ${}\operatorname {Im} \,{\left(z+w\right)}=\operatorname {Im} \,{\left(z\right)}+\operatorname {Im} \,{\left(w\right)}$.
4. Für ${}r\in \mathbb {R}$ ist

   $\operatorname {Re} \,{\left(rz\right)}=r\operatorname {Re} \,{\left(z\right)}{\text{ und }}\operatorname {Im} \,{\left(rz\right)}=r\operatorname {Im} \,{\left(z\right)}.$

5. Es ist ${}z=\operatorname {Re} \,{\left(z\right)}$ genau dann, wenn ${}z\in \mathbb {R}$ ist, und dies ist genau dann der Fall, wenn ${}\operatorname {Im} \,{\left(z\right)}=0$ ist.

Beweis

Siehe Aufgabe 5.29.

$\Box$

Definition Referenznummer erstellen

Die Abbildung

${\mathbb {C} }\longrightarrow {\mathbb {C} },\,z=a+b{\mathrm {i} }\longmapsto {\overline {z}}:=a-b{\mathrm {i} },$

heißt komplexe Konjugation.

Zu ${}z$ heißt ${}{\overline {z}}$ die konjugiert-komplexe Zahl von ${}z$. Geometrisch betrachtet ist die komplexe Konjugation zu ${}z\in {\mathbb {C} }$ einfach die Achsenspiegelung an der reellen Achse.

Lemma Referenznummer erstellen

Für die komplexe Konjugation gelten die folgenden Rechenregeln (für beliebige ${}z,w\in {\mathbb {C} }$).

1. Es ist ${}{\overline {z+w}}={\overline {z}}+{\overline {w}}$.
2. Es ist ${}{\overline {-z}}=-{\overline {z}}$.
3. Es ist ${}{\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}}$.
4. Für ${}z\neq 0$ ist ${}{\overline {1/z}}=1/{\overline {z}}$.
5. Es ist ${}{\overline {\overline {z}}}=z$.
6. Es ist ${}{\overline {z}}=z$ genau dann, wenn ${}z\in \mathbb {R}$ ist.

Beweis

Siehe Aufgabe 5.36.

$\Box$

Lemma Referenznummer erstellen

Für eine komplexe Zahl ${}z$ gelten die folgenden Beziehungen.

1. Es ist ${}{\overline {z}}=\operatorname {Re} \,{\left(z\right)}-{\mathrm {i} }\operatorname {Im} \,{\left(z\right)}$.
2. Es ist ${}\operatorname {Re} \,{\left(z\right)}={\frac {z+{\overline {z}}}{2}}$.
3. Es ist ${}\operatorname {Im} \,{\left(z\right)}={\frac {z-{\overline {z}}}{2{\mathrm {i} }}}$.

Beweis

Siehe

Aufgabe *****.

{{:Kurs:Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Komplexe Zahlen/Konjugation/Realteil Imaginärteil/Fakt/Beweis/Aufgabe/Aufgabereferenznummer/Komplexe Zahlen/Konjugation/Realteil Imaginärteil/Fakt/Beweis/Aufgabe/Aufgabereferenznummer}}

$\Box$

Das Quadrat ${}d^{2}$ einer reellen Zahl ist stets nichtnegativ, und die Summe von zwei nichtnegativen reellen Zahlen ist wieder nichtnegativ. Zu einer nichtnegativen reellen Zahl ${}c$ gibt es eine eindeutige nichtnegative Quadratwurzel ${}{\sqrt {c}}$, siehe Aufgabe 8.9  (das werden wir später beweisen) Daher liefert folgende Definition eine wohldefinierte nichtnegative reelle Zahl.

Definition Referenznummer erstellen

Zu einer komplexen Zahl

${}z=a+b{\mathrm {i} }\,$

ist der Betrag durch

${}\vert {z}\vert ={\sqrt {a^{2}+b^{2}}}\,$

definiert.

Der Betrag einer komplexen Zahl ${}z$ ist aufgrund des Satzes des Pythagoras der Abstand von ${}z$ zum Nullpunkt ${}0=(0,0)$. Insgesamt ist der Betrag eine Abbildung

${\mathbb {C} }\longrightarrow \mathbb {R} _{\geq 0},\,z\longmapsto \vert {z}\vert .$

Die Menge aller komplexen Zahlen mit einem bestimmten Betrag bilden einen Kreis mit dem Nullpunkt als Mittelpunkt und mit dem Betrag als Radius. Insbesondere bilden alle komplexen Zahlen mit dem Betrag ${}1$ den komplexen Einheitskreis.

Lemma Lemma 5.20 ändern

Für den Betrag von komplexen Zahlen gelten folgende Eigenschaften.

1. Es ist ${}\vert {z}\vert ={\sqrt {z\ {\overline {z}}}}$.
2. Für reelles ${}z$ stimmen reeller und komplexer Betrag überein.
3. Es ist ${}\vert {z}\vert =0$ genau dann, wenn ${}z=0$ ist.
4. Es ist ${}\vert {z}\vert =\vert {\overline {z}}\vert$.
5. Es ist ${}\vert {zw}\vert =\vert {z}\vert \cdot \vert {w}\vert$.
6. Für ${}z\neq 0$ ist ${}\vert {1/z}\vert =1/\vert {z}\vert$.
7. Es ist ${}\vert {\operatorname {Re} \,{\left(z\right)}}\vert ,\vert {\operatorname {Im} \,{\left(z\right)}}\vert \leq \vert {z}\vert$.
8. Es ist ${}\vert {z+w}\vert \leq \vert {z}\vert +\vert {w}\vert$ (Dreiecksungleichung).

Beweis

Wir zeigen die Dreiecksungleichung, für die anderen Aussagen siehe Aufgabe 5.31. Zunächst gilt nach (7) für jede komplexe Zahl ${}u$ die Abschätzung ${}\operatorname {Re} \,{\left(u\right)}\leq \vert {u}\vert$. Daher ist

${}\operatorname {Re} \,{\left(z{\overline {w}}\right)}\leq \vert {z}\vert \vert {w}\vert \,,$

und somit ist

${}{\begin{aligned}\vert {z+w}\vert ^{2}&=(z+w)({\overline {z}}+{\overline {w}})\\&=z{\overline {z}}+z{\overline {w}}+w{\overline {z}}+w{\overline {w}}\\&=\vert {z}\vert ^{2}+2\operatorname {Re} \,{\left(z{\overline {w}}\right)}+\vert {w}\vert ^{2}\\&\leq \vert {z}\vert ^{2}+2\vert {z}\vert \vert {w}\vert +\vert {w}\vert ^{2}\\&=(\vert {z}\vert +\vert {w}\vert )^{2}.\end{aligned}}$

Durch Wurzelziehen ergibt sich die gewünschte Abschätzung.

$\Box$

Fußnoten